ဂျီဩမေတြီဆိုသည်မှာ

အားဖြင့် Benjamin Anderson ဩဂုတ် 6, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် ဂျီဩမေတြီဆိုလိုရင်းမှာ အဘယ်နည်း၊ ၎င်းကို တွက်ချက်ပုံနှင့် ဂျီဩမေတြီသဏ္ဍာန်နှင့် ဂဏန်းသင်္ချာဆိုလိုမှုတို့အကြား ကွာခြားချက်က အဘယ်နည်း။ ဂျီဩမေတြီဆိုလိုရင်းကို အဆင့်ဆင့်ဖြေရှင်းထားသော လေ့ကျင့်ခန်းနှင့် ဤဆိုလိုချက်အမျိုးအစား၏ ဂုဏ်သတ္တိများကား အဘယ်နည်း။ နောက်ဆုံးတွင်၊ မည်သည့်ဒေတာအစုံ၏ဂျီဩမေတြီပျမ်းမျှကိုတွက်ချက်ရန်ဂဏန်းပေါင်းစက်ကိုသင်တွေ့လိမ့်မည်။

ဂျီဩမေတြီဆိုသည်မှာ အဘယ်နည်း။

ဂျီဩမေတြီဆိုလိုသည်မှာ သရုပ်ဖော်ကိန်းဂဏန်းများ၏ ဗဟိုချက်ကို တိုင်းတာခြင်းဖြစ်သည်။ ကိန်းဂဏန်းအချက်အလက်အစုတစ်ခု၏ ဂျီဩမေတြီဆိုလိုသည်မှာ တန်ဖိုးအားလုံး၏ ထုတ်ကုန်၏ နံပါတ်မြောက်အမြစ်နှင့် ညီမျှသည်။

ဂျီဩမေတြီပျမ်းမျှကို စီးပွားရေးလုပ်ငန်းဘဏ္ဍာရေးတွင် သုံးသည်

ထို့ကြောင့် ဂျီဩမေတြီပျမ်းမျှအတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်။

နမူနာရှိ ဒေတာအားလုံး အပြုသဘောရှိမှသာ ဂျီဩမေတြီပျမ်းမျှအား တွက်ချက်နိုင်သည်။ အဘယ်ကြောင့်ဆိုသော် တန်ဖိုးတစ်ခုသည် အနုတ်လက္ခဏာဖြစ်ပါက၊ root တွင် အနုတ်အဖြေတစ်ခု သို့မဟုတ် အဖြေမရှိနိုင်သောကြောင့်၊ တစ်ဖက်တွင်၊ ဒေတာသည် သုညဖြစ်ပါက ဒေတာ၏အမြှောက်သည် သုညကိုပေးမည်ဖြစ်ပြီး ထို့ကြောင့်၊ ဂျီဩမေတြီဆိုလိုရင်းမှာ 0 နှင့် ညီမျှမည်ဖြစ်သည်။

ဂျီဩမေတြီဆိုလိုသည်မှာ တစ်ခုတည်းသော ကိန်းဂဏန်းအမျိုးအစားမဟုတ်ပါ၊ ဂဏန်းသင်္ချာဆိုလို၊ အလေးချိန်တွက်ဆ၊ စတုရန်းပျမ်းမျှနှင့် ဟာမိုနီဆိုလိုများလည်း ရှိပါသည်။

ဂျီဩမေတြီပျမ်းမျှနှင့် ဂဏန်းသင်္ချာဆိုလို ကွာခြားချက်

ဂျီဩမေတြီပျမ်းမျှနှင့် ဂဏန်းသင်္ချာဆိုလိုချက်အကြား အဓိကကွာခြားချက်မှာ ဂျီဩမေတြီဆိုလိုသည်မှာ ဂဏန်းသင်္ချာပျမ်းမျှထက် လွန်ကဲသောတန်ဖိုးများထက် လွန်ကဲသောတန်ဖိုးများကို အာရုံခံစားနိုင်မှုနည်းသည်။ ထို့အပြင်၊ ဂဏန်းသင်္ချာပျမ်းမျှအား အနုတ်တန်ဖိုးများနှင့် သုညတန်ဖိုးများဖြင့် တွက်ချက်နိုင်သော်လည်း ဂျီဩမေတြီပျမ်းမျှအား အပေါင်းတန်ဖိုးများဖြင့်သာ တွက်ချက်နိုင်ပါသည်။

အလားတူ၊ ဂျီဩမေတြီဆိုလိုသည်မှာ ယေဘူယျအားဖြင့် တူညီသောဒေတာအတွဲအတွက် ဂဏန်းသင်္ချာပျမ်းမျှထက် နိမ့်ပါသည်။

ဂျီဩမေတြီပျမ်းမျှတွက်ချက်မှုသည် ပိုမိုရှုပ်ထွေးသောကြောင့် ၎င်း၏စာရင်းအင်းဆိုင်ရာ အရေးပါမှုသည် အဓိပ္ပာယ်ဖွင့်ဆိုရန် ပိုမိုခက်ခဲကြောင်းကိုလည်း သတိပြုသင့်သည်။

အတိုချုပ်ပြောရလျှင် ဂျီဩမေတြီပျမ်းမျှသည် ဂဏန်းသင်္ချာပျမ်းမျှနှင့်နှိုင်းယှဉ်လျှင် အားသာချက်များနှင့် အားနည်းချက်များရှိပြီး ဒေတာ၏သဘောသဘာဝပေါ် မူတည်၍ ဤသို့မဟုတ်ထိုပျမ်းမျှအား တွက်ချက်ရန် သင့်လျော်မည်ဖြစ်သည်။

ဂျီဩမေတြီကို တွက်နည်း

ဂျီဩမေတြီပျမ်းမျှအား တွက်ချက်ရန်၊ အောက်ပါအဆင့်များကို လုပ်ဆောင်ရပါမည်-

နမူနာရှိ ကိန်းဂဏန်းအချက်အလက်အားလုံး၏ ထုတ်ကုန်ကို တွက်ချက်ပါ။
တွက်ချက်ထားသောထုတ်ကုန်၏ nth root ကိုရှာပါ။
ရရှိသောရလဒ်မှာ ကိန်းဂဏန်းနမူနာ၏ ဂျီဩမေတြီပျမ်းမျှဖြစ်သည်။

သင်တွေ့မြင်ရသည့်အတိုင်း၊ ဒေတာအစုတစ်ခု၏ ဂျီဩမေတြီပျမ်းမျှအား ရှာဖွေခြင်းသည် ဂဏန်းပေါင်းစက် သို့မဟုတ် ကွန်ပျူတာပရိုဂရမ်တစ်ခုဖြင့် အတော်လေးရိုးရှင်းသည်၊ အဘယ်ကြောင့်ဆိုသော် သင်သည် ထုတ်ကုန်တစ်ခုနှင့် အမြစ်တစ်ခုကို တွက်ချက်ရန်သာ လိုအပ်သောကြောင့်ဖြစ်သည်။ ဆန့်ကျင်ဘက်အနေနှင့် လက်ဖြင့် တွက်ချက်ရန် အလွန်ပင်ပန်းပါသည်။

👉 ထို့ကြောင့် ဒေတာအစုတစ်ခု၏ ဂျီဩမေတြီပျမ်းမျှကို တွက်ချက်ရန် အောက်ဖော်ပြပါ ဂဏန်းပေါင်းစက်ကို အသုံးပြုရန် အကြံပြုအပ်ပါသည်။

Geometric Mean ဥပမာ

ဂျီဩမေတြီဆိုလိုအားနှင့်ပတ်သက်သော သီအိုရီကို ကျွန်ုပ်တို့တွေ့မြင်ပြီးသည်နှင့်၊ ဂျီဩမေတြီဆိုလိုအား မည်သို့ရနိုင်သည်ကို အတိအကျ သိနိုင်စေရန် ဥပမာတစ်ခု ပြုလုပ်ပါမည်။

လွန်ခဲ့သည့်ငါးနှစ်အတွင်း ကုမ္ပဏီတစ်ခု၏ စီးပွားရေးရလဒ်များကို သိရှိသည်။ ပထမနှစ်တွင် ကုမ္ပဏီမှ အမြတ်ငွေ ၁၀ ရာခိုင်နှုန်း ရရှိခဲ့ပြီး ဒုတိယနှစ်တွင် အမြတ်ငွေ ၂၃ ရာခိုင်နှုန်း ရရှိကာ တတိယနှစ်တွင် အမြတ်ငွေ ၁၆ ရာခိုင်နှုန်းနှင့် စတုတ္ထနှစ်တွင် အမြတ်အစွန်း ၇ ရာခိုင်နှုန်း ရရှိခဲ့ကြောင်း၊ ပဉ္စမနှစ်တွင် 20% ပြန်လာခဲ့သည်။ ရာခိုင်နှုန်းအားလုံး၏ ပျမ်းမျှအား တွက်ချက်ရန် သင့်အား တောင်းဆိုထားသည်။

ကျွန်ုပ်တို့မြင်ခဲ့ရသည့်အတိုင်း ရာခိုင်နှုန်းများ၏ ပျမ်းမျှအား တွက်ချက်ရန်၊ သင်သည် ဂဏန်းသင်္ချာပျှမ်းမျှကို အသုံးမပြုသင့်ဘဲ ဂျီဩမေတြီပျှမ်းမျှဖြင့် တွက်ချက်ခြင်းကို လုပ်ဆောင်ပါ။

ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် ဂျီဩမေတြီပျမ်းမျှ ဖော်မြူလာကို အသုံးပြုသည်-

$MG=\sqrt[n]{\prod_{i=1}^Nx_i}=\sqrt[n]{x_1\cdot x_2\cdot \ldots x_n}$

ကျွန်ုပ်တို့သည် နမူနာတန်ဖိုးများကို ဖော်မြူလာတွင် အစားထိုးပြီး တွက်ချက်မှုကို လုပ်ဆောင်သည်-

$MG=\sqrt[5]{1,10\cdot 1,23\cdot 1,16\cdot 1,07\cdot 1,20}=1,15 \ \longrightarrow \ 15 \%$

ကျွန်ုပ်တို့တွင် ဒေတာအချက်ငါးခုရှိသည်ကို သတိပြုပါ၊ ထို့ကြောင့် ပဉ္စမမြောက်အမြစ်ကို တွက်ချက်နေပါသည်။

ဂျီဩမေတြီပျမ်းမျှ ကိန်းဂဏာန်းရလဒ်သည် 1.15 ဖြစ်ပြီး၊ ဆိုလိုသည်မှာ ကုမ္ပဏီသည် တစ်နှစ်လျှင် ပျမ်းမျှ စီးပွားရေးတိုးတက်မှု 15% ကို ကြုံတွေ့နေရသည်။

တန်ဖိုးများအားလုံးသည် အပြုသဘောဖြစ်သောကြောင့် ဂျီဩမေတြီဆိုလိုရင်းကို ရနိုင်သော်လည်း မည်သည့်ရာခိုင်နှုန်းမဆို အနှုတ်ဖြစ်ပါက ကိန်းပြည့်ဒဿမအဖြစ် ကိန်းဂဏန်းတွင် ဒေတာကို အပြုသဘောဒဿမအဖြစ် ထားရှိရမည်ဖြစ်ပါသည်။ သုညနှင့် ညီမျှသည်။ ဥပမာအားဖြင့်၊ တိုးတက်မှုနှုန်း -30% ကို 0.70 (1-0.3=0.7) အဖြစ် ဖော်မြူလာတွင် ဖော်ပြသင့်သည်။

Geometric Mean ဂဏန်းတွက်စက်

၎င်း၏ ဂျီဩမေတြီ ပျမ်းမျှ ကိန်းဂဏန်းကို ရှာရန် အောက်ပါ ဂဏန်းပေါင်းစက်တွင် မည်သည့်နမူနာ ကိန်းဂဏန်းကိုမဆို ချိတ်ဆက်ပါ။ ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။ တန်ဖိုးသည် အနှုတ် သို့မဟုတ် သုညဖြစ်လျှင် ဂျီဩမေတြီဆိုလိုရင်းကို သင်မဆုံးဖြတ်နိုင်ကြောင်း သတိရပါ။

ဂျီဩမေတြီ ဆိုလိုရင်း၏ ဂုဏ်သတ္တိများ

ဂျီဩမေတြီဆိုလိုရင်းတွင် အောက်ပါလက္ခဏာများရှိသည်။

၎င်းသည် ပျမ်းမျှရာခိုင်နှုန်းများ သို့မဟုတ် အညွှန်းကိန်းများကို ရှာဖွေရန်အတွက် အလွန်အသုံးဝင်သော ပျမ်းမျှအမျိုးအစားတစ်ခုဖြစ်သည်။

အချက်အလက်အားလုံး အပြုသဘောရှိမှသာ တွက်ချက်နိုင်သည်။

a နှင့် b ၏ ဂျီဩမေတြီ ကိန်းဂဏန်းနှစ်ခု၏ ဂျီဩမေတြီဆိုလိုရင်းမှာ အခြမ်းသည် a နှင့် b တိုင်းတာသော စတုဂံကဲ့သို့ ဧရိယာတူညီသော စတုရန်းတစ်ခု၏ ဘေးဘက်ဖြစ်သည်။

$MG(a,b)=\sqrt{a\cdot b}$

ဂဏန်းသုံးလုံး၏ ဂျီဩမေတြီဆိုလိုရင်းမှာ a , b နှင့် c ၏ ဂျီဩမေတြီအဓိပ္ပါယ်မှာ ထုထည်ပမာဏသည် အခြမ်း a , b နှင့် c နှင့် ညီမျှသော cube ၏ ဘေးဘက်ဖြစ်သည်။

$MG(a,b,c)=\sqrt[3]{a\cdot b \cdot c}$

ဒေတာအစုတစ်ခု၏ ဂျီဩမေတြီပျမ်းမျှ၏ လော့ဂရစ်သမ်သည် တူညီသောအစု၏ လော့ဂရစ်သမ်၏ ဂဏန်းသင်္ချာကိန်းဂဏန်းကို ပေးသည်။

တန်ဖိုးအစုတစ်ခု၏ ဂျီဩမေတြီဆိုလိုသည်မှာ ဂဏန်းသင်္ချာဆိုလိုချက်ထက် အမြဲလျော့နည်းနေမည် သို့မဟုတ် ညီမျှသည်။

$\sqrt[N]{x_1\cdot x_2\ldots x_N}\leq \cfrac{x_1+x_2+\ldots+x_N}{N}$

အလေးချိန်ရှိသော ဂျီဩမေတြီပျမ်းမျှအား ဂျီဩမေတြီဆိုလိုရင်းအတိုင်း တွက်ချက်သည်၊ သို့သော် ကိန်းဂဏန်းတန်ဖိုးများကို တွက်ဆရန် အချက်အလက်တစ်ခုစီ၏ ထပ်ကိန်းတွင် အလေးများကို ပေါင်းထည့်ခြင်းဖြင့်။

$\displaystyle \left(\prod_{i=1}^n{x_i}^{\alpha_i}\right)^{\frac{1}{\sum_i{\alpha_i}}}= \left({x_1}^{\alpha_1}{x_2}^{\alpha_2}\dots{x_n}^{\alpha_n}\right)^{ \frac{1}{\alpha_1+ \dots+ \alpha_n}} \left}}$

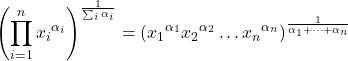
Excel တွင် geometric mean တွက်ချက်ပါ။

နောက်ဆုံးအနေနဲ့၊ Excel ပရိုဂရမ်ကိုသုံးပြီး ဒေတာအတွဲတစ်ခုရဲ့ ဂျီဩမေတြီကို ဘယ်လိုရှာရမလဲဆိုတာ ကြည့်ကြရအောင်။

Excel ရှိ ဂျီဩမေတြီပျမ်းမျှအား တွက်ချက်ရန်၊ သင်သည် MEANS.GEOM လုပ်ဆောင်ချက်ကို အသုံးပြုရန် လိုအပ်သည်။ သင်ယူလိုသော ဂျီဩမေတြီပျမ်းမျှတန်ဖိုးအားလုံးကို ရိုးရှင်းစွာထည့်ပါ၊ လုပ်ဆောင်ချက်သည် ဂျီဩမေတြီဆိုလိုရင်းရလဒ်ကို ပြန်ပေးလိမ့်မည်။

ဥပမာ၊ အထက်ဖော်ပြပါ ဥပမာ၏ ဂျီဩမေတြီဆိုလိုရင်းကို ဆုံးဖြတ်ရန်၊ Excel အကွက် =MEDIA.GEOM(1.1;1.23;1.16;1.07;1.20) တွင် ရေးရပါမည်။

မည်သည့်တန်ဖိုးများမဆို သုည သို့မဟုတ် အနုတ်ဖြစ်ပါက လုပ်ဆောင်ချက်သည် အမှားတစ်ခု ပြန်ဖြစ်သွားမည်ဖြစ်ကြောင်း မှတ်သားထားသင့်သည်။

သင်တွေ့မြင်ရသည့်အတိုင်း၊ Excel ဖြင့် ဂျီဩမေတြီပျမ်းမျှကို တွက်ချက်ရန် ပိုမိုလွယ်ကူပြီး မြန်ဆန်သည်၊ အဘယ်ကြောင့်ဆိုသော် သင်သည် စာရွက်တစ်ခုပေါ်သို့ ဒေတာကို ကူးယူပြီး ဖော်မြူလာကို အသုံးပြုရန် လိုအပ်သောကြောင့် ဖြစ်သည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။