Excel တွင် ဂျီဩမေတြီဖြန့်ဝေနည်းကို အသုံးပြုနည်း

ဂျီဩမေတြီ ဖြန့်ဝေမှုသည် Bernoulli စမ်းသပ်မှု ဆက်တိုက်တွင် ပထမဆုံး အောင်မြင်မှု မကြုံမီ အချို့သော ကျရှုံးမှု အများအပြားကို တွေ့ကြုံရနိုင်ခြေကို ဖော်ပြသည်။

Bernoulli စမ်းသပ်မှု သည် ဖြစ်နိုင်ချေ ရလဒ် နှစ်ခုသာရှိသော စမ်းသပ်မှုဖြစ်ပြီး – “ အောင်မြင်မှု” သို့မဟုတ် “ ကျရှုံးခြင်း” – စမ်းသပ်မှုပြုလုပ်သည့်အချိန်တိုင်း အောင်မြင်နိုင်ခြေသည် အတူတူပင်ဖြစ်ပါသည်။

Bernoulli စာစီစာကုံး၏ ဥပမာတစ်ခုသည် အကြွေစေ့ပစ်ခြင်း ဖြစ်သည်။ ဒင်္ဂါးသည် ခေါင်းနှစ်လုံးပေါ်တွင်သာ ဆင်းသက်နိုင်သည် (ကျွန်ုပ်တို့သည် ခေါင်းများကို “ တိုက်သည်” နှင့် “ ပျက်ကွက်” ဟု ခေါ်နိုင်သည်) နှင့် ဒင်္ဂါးပြားသည် မျှတသည်ဟု ယူဆကာ လှန်လိုက်တိုင်းတွင် အောင်မြင်နိုင်ခြေသည် 0.5 ဖြစ်သည်။

ကျပန်းပြောင်းလဲနိုင်သော X သည် ဂျီဩမေတြီဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်ပါက၊ ပထမအောင်မြင်မှုမတွေ့ကြုံမီ k ကျရှုံးမှုဖြစ်နိုင်ခြေကို အောက်ပါဖော်မြူလာဖြင့် ရှာတွေ့နိုင်သည်-

P(X=k) = (1-p) ^kp

ရွှေ-

• k: ပထမမအောင်မြင်မီ ကျရှုံးမှုအရေအတွက်
• p- စမ်းသပ်မှုတစ်ခုစီတွင် အောင်မြင်မှုဖြစ်နိုင်ခြေ

အောက်ဖော်ပြပါနမူနာများသည် Excel တွင် ဂျီဩမေတြီဖြန့်ဖြူးမှုနှင့် ပတ်သက်သော ဖြစ်နိုင်ခြေများကို တွက်ချက်နည်းကို ပြသထားသည်။

ဥပမာ 1- အကြွေစေ့ကိုလှန်ပါ။

အကြွေစေ့တစ်ပြားကို ပစ်ချလိုက်ပြီး အကြွေစေ့တစ်ခု ခေါင်းပေါ်မလာမီ “လွဲချော်မှု” သုံးကြိမ်တိတိ အချိန်ယူရနိုင်ချေကို သိချင်သည်ဆိုပါစို့။

ဤဖြစ်နိုင်ခြေကို တွက်ချက်ရန် အောက်ပါဖော်မြူလာကို ကျွန်ုပ်တို့ အသုံးပြုပါမည်။

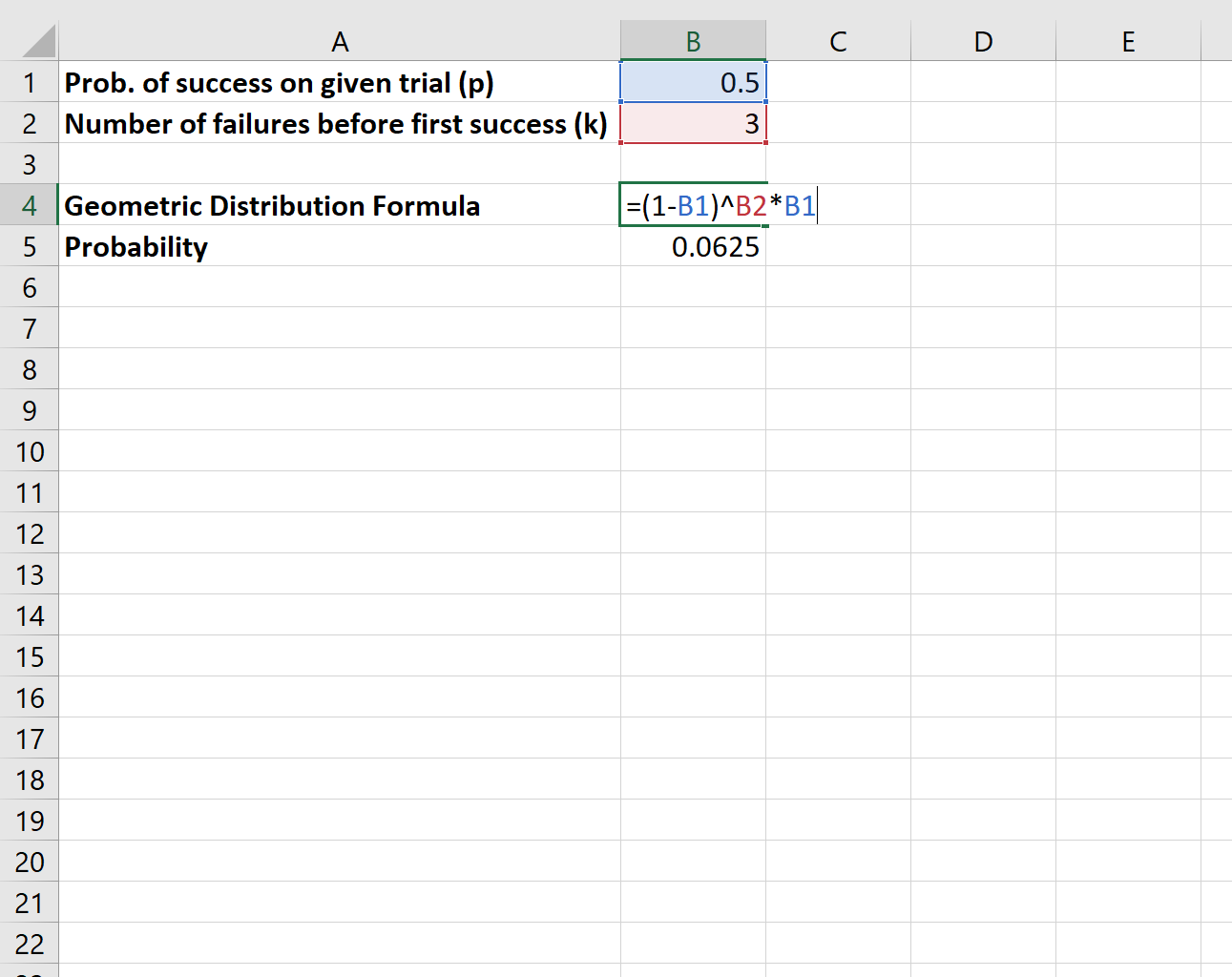
အကြွေစေ့ခေါင်းများပေါ်မလာမချင်း “ လွဲချော်မှု” သုံးခုကြုံရသည့်ဖြစ်နိုင်ခြေမှာ 0.0625 ဖြစ်သည်။

ဥပမာ 2- အလွတ်ပစ်ပစ်ခြင်း။

အချို့သော ဘတ်စကတ်ဘော ကစားသမားတစ်ဦးသည် ၎င်း၏ အလွတ်ပစ်လွှတ်မှု၏ 60% ကို ပြုလုပ်သည်ဆိုပါစို့။ ကစားသမားသည် နောက်ဆုံးတစ်ကြိမ် ပြုလုပ်သည့်အချိန်အထိ အလွတ်ပစ်လေးခုကို လွတ်သွားသည့် ဖြစ်နိုင်ခြေအဘယ်နည်း။

ဤဖြစ်နိုင်ခြေကို တွက်ချက်ရန် အောက်ပါဖော်မြူလာကို ကျွန်ုပ်တို့ အသုံးပြုပါမည်။

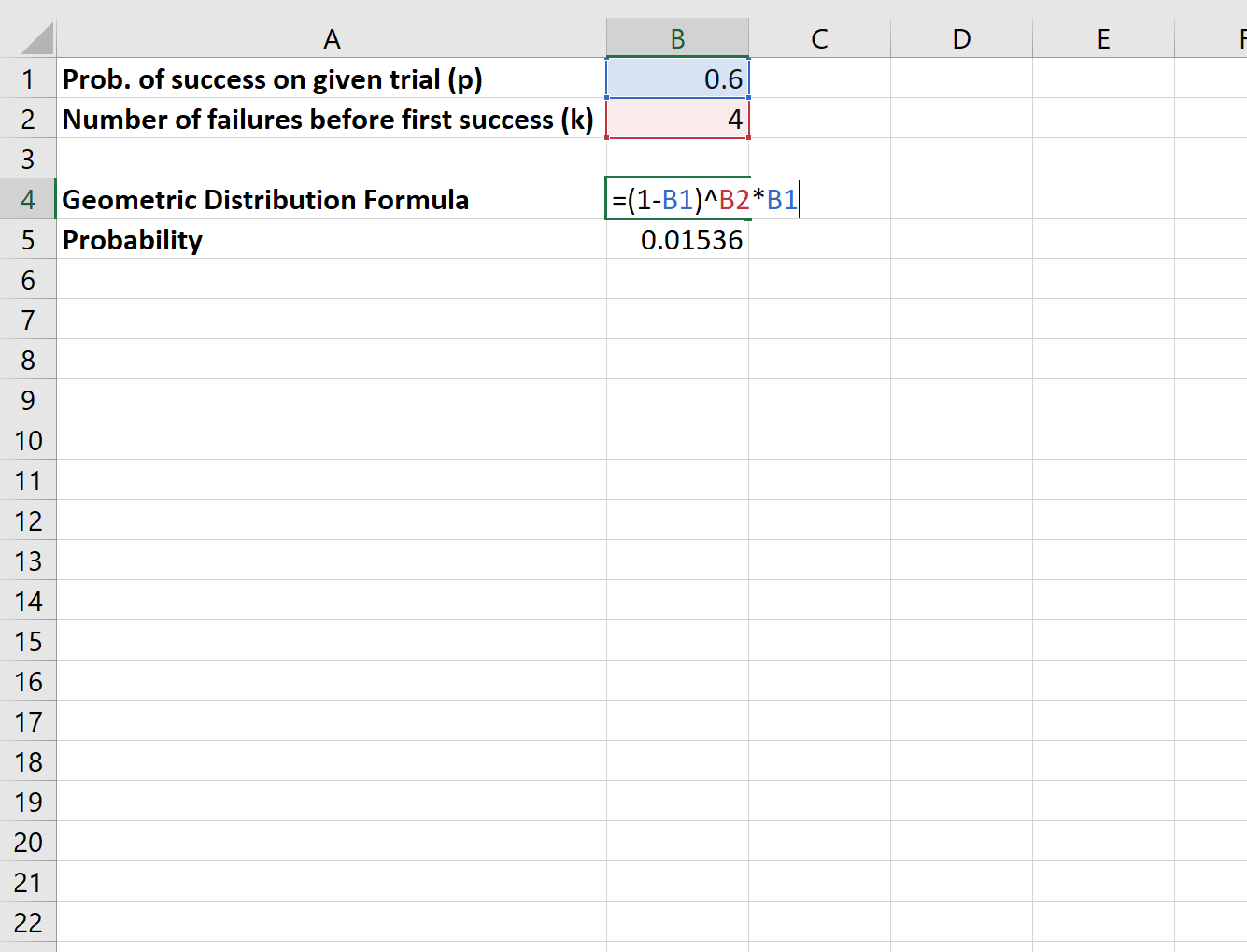
ကစားသမားသည် နောက်ဆုံးတွင် တစ်ကြိမ်ပြုလုပ်သည့်အချိန်အထိ အလွတ်ပစ်ချက်လေးချက်လွတ်သွားနိုင်သည့်ဖြစ်နိုင်ခြေမှာ 0.01536 ဖြစ်သည်။

ဥပမာ ၃- ဥပဒေတစ်ရပ်ကို ထောက်ခံခြင်း။

သုတေသီတစ်ဦးသည် ဥပဒေတစ်ရပ်ရပ်ကို ထောက်ခံခြင်းရှိမရှိ လူများကိုမေးရန် စာကြည့်တိုက်အပြင်ဘက်တွင် စောင့်ဆိုင်းနေသည်ဆိုပါစို့။ ဥပဒေကို ပံ့ပိုးပေးထားသည့် ပုဂ္ဂိုလ်တစ်ဦးဖြစ်နိုင်ခြေမှာ p = 0.2 ဖြစ်သည်။ သုတေသီ ဟောပြောသူ စတုတ္ထပုဂ္ဂိုလ်သည် ဥပဒေကို ထောက်ခံသူဖြစ်နိုင်ခြေ မည်မျှရှိသနည်း။

ဤဖြစ်နိုင်ခြေကို တွက်ချက်ရန် အောက်ပါဖော်မြူလာကို ကျွန်ုပ်တို့ အသုံးပြုပါမည်။

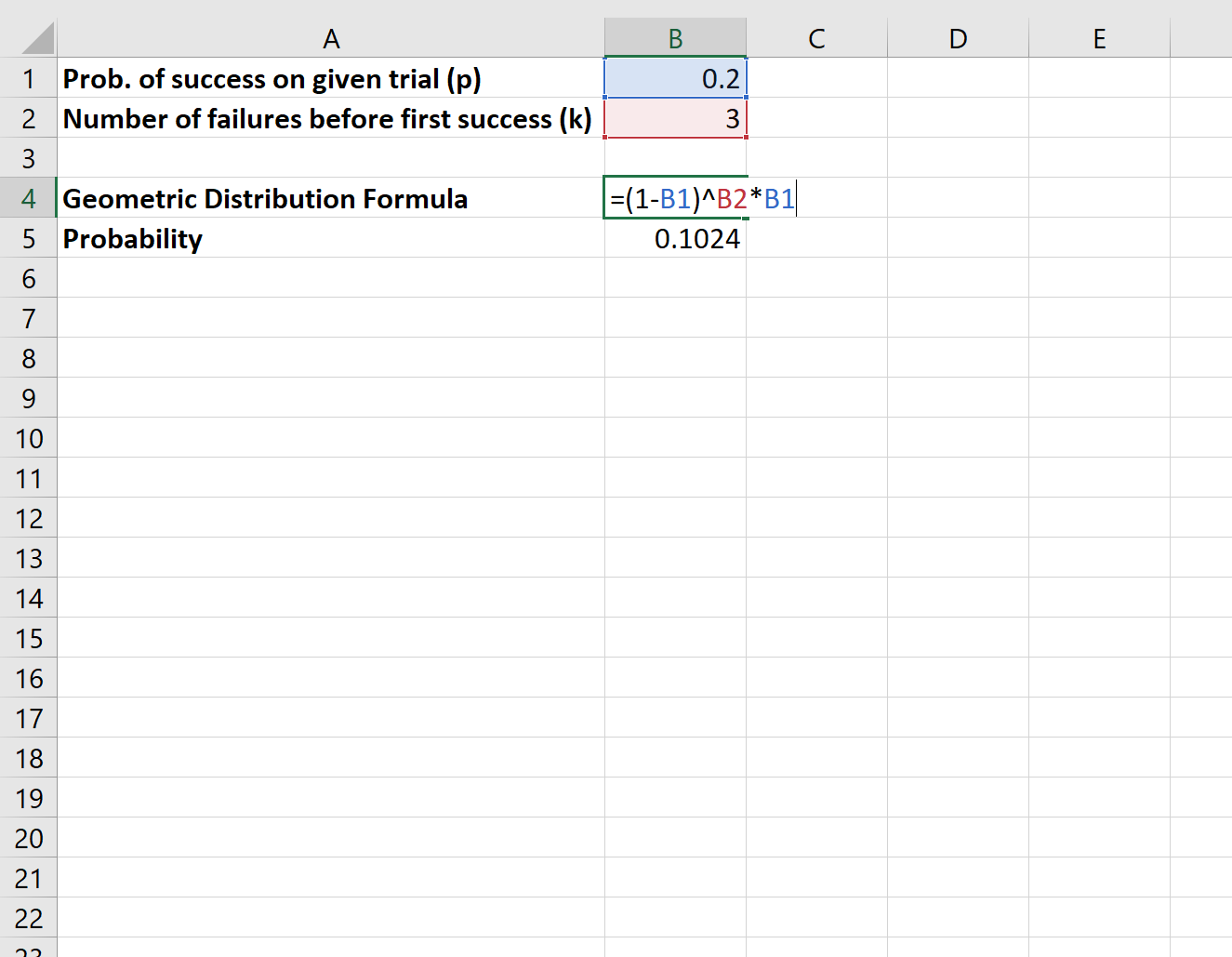
သုတေသနပညာရှင်စတုတ္ထလူနှင့်စကားပြောသောဖြစ်နိုင်ခြေသည် ဥပဒေအား ပံ့ပိုးရန် ပထမဆုံးဖြစ်နိုင်ခြေမှာ 0.1024 ဖြစ်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

ဂျီဩမေတြီ ဖြန့်ဖြူးခြင်းအကြောင်း မိတ်ဆက်
ဂျီဩမေတြီဖြန့်ဝေဂဏန်းတွက်စက်
ဂျီဩမေတြီဖြန့်ဖြူးခြင်း၏ ခိုင်မာသော ဥပမာ ၅