Poisson ဖြန့်ဖြူးမှုမိတ်ဆက်

Poisson ဖြန့်ဖြူးမှုသည် စာရင်းဇယားများတွင် ရေပန်းအစားဆုံး ဖြန့်ဝေမှုတစ်ခုဖြစ်သည်။

Poisson ဖြန့်ဖြူးမှုကို နားလည်ရန် Poisson စမ်းသပ်မှုများကို ဦးစွာနားလည်ရန် အထောက်အကူဖြစ်စေပါသည်။

ငါးစမ်းသပ်မှုများ

Poisson စမ်းသပ်ချက် သည် အောက်ပါဂုဏ်သတ္တိများပါရှိသော စမ်းသပ်မှုတစ်ခုဖြစ်သည်။

• စမ်းသပ်မှု၏ အောင်မြင်မှုအရေအတွက်ကို ရေတွက်နိုင်သည်။
• သတ်မှတ်ထားသော အချိန် (သို့မဟုတ် အာကာသ) ကြားကာလတစ်ခုအတွင်း ဖြစ်ပွားခဲ့သော ပျမ်းမျှအောင်မြင်မှုအရေအတွက်ကို သိပါသည်။
• ရလဒ်တစ်ခုစီသည် သီးခြားဖြစ်သည်။
• အောင်မြင်သော ဖြစ်ပျက်မှု၏ ဖြစ်နိုင်ခြေသည် ကြားကာလ၏ အရွယ်အစားနှင့် အချိုးကျပါသည်။

Poisson စမ်းသပ်မှုတစ်ခု၏ ဥပမာတစ်ခုသည် ဆေးရုံတစ်ခုတွင် တစ်နာရီလျှင် မွေးဖွားမှုအရေအတွက်ဖြစ်သည်။ ဥပမာအားဖြင့်၊ ဆေးရုံတစ်ခုသည် တစ်နာရီလျှင် ပျမ်းမျှ ၁၀ ဦး မွေးသည်ဆိုပါစို့။ ၎င်းသည် အောက်ဖော်ပြပါ ဂုဏ်သတ္တိလေးခုပါရှိသောကြောင့် ၎င်းသည် Poisson စမ်းသပ်မှုတစ်ခုဖြစ်သည်။

• စမ်းသပ်မှု၏အောင်မြင်မှုအရေအတွက်ကိုရေတွက်နိုင်သည် – ကျွန်ုပ်တို့သည်မွေးဖွားမှုအရေအတွက်ကိုရေတွက်နိုင်သည်။
• တိကျသောအချိန်ကြားကာလတစ်ခုအတွင်း ဖြစ်ပွားသော ပျမ်းမျှမွေးဖွားမှုအရေအတွက်ကို သိရှိနိုင်သည် – တစ်နာရီလျှင် ပျမ်းမျှမွေးဖွားမှု ၁၀ ကြိမ်ရှိကြောင်း သိရှိရပါသည်။
• ရလဒ်တစ်ခုစီသည် အမှီအခိုကင်းသည်- မိခင်တစ်ဦးသည် သတ်မှတ်နာရီအတွင်း ကလေးမွေးဖွားနိုင်ခြေသည် အခြားမိခင်တစ်ဦးမွေးဖွားမည့်ဖြစ်နိုင်ခြေနှင့် ကင်းကွာသည်။
• အောင်မြင်မှုတစ်ခု၏ဖြစ်နိုင်ခြေသည် ကြားကာလ၏အရွယ်အစားနှင့်အချိုးကျဖြစ်ပါသည်- အချိန်ကြားကာလပိုရှည်လေ၊ မွေးဖွားမှုဖြစ်နိုင်ခြေပိုများလေဖြစ်သည်။

ဤ Poisson စမ်းသပ်မှုနှင့်ပတ်သက်၍ ဖြစ်နိုင်ခြေရှိသောမေးခွန်းများကိုဖြေဆိုရန် Poisson ဖြန့်ဖြူးမှုကို ကျွန်ုပ်တို့အသုံးပြုနိုင်သည်-

• သတ်မှတ်နာရီအတွင်း 12 ကြိမ်ထက်ပိုမွေးဖွားနိုင်ခြေအဘယ်နည်း။
• သတ်မှတ်နာရီအတွင်း 5 ကြိမ်ထက်နည်းသော မွေးဖွားမှု ဖြစ်နိုင်ခြေ မည်မျှရှိသနည်း။
• သတ်မှတ်နာရီအတွင်း ၈ နှစ်မှ ၁၁ နှစ်ကြား ကလေးမွေးဖွားနိုင်ခြေ မည်မျှရှိသနည်း။

ငါးဖြန့်ဖြူးရေး

Poisson ဖြန့်ဖြူးမှုသည် ပေးထားသည့်အချိန်ကြားကာလတစ်ခုအတွင်း k အောင်မြင်မှုများရရှိရန် ဖြစ်နိုင်ခြေကို ဖော်ပြသည်။

ကျပန်းပြောင်းလဲနိုင်သော X သည် Poisson ဖြန့်ဝေမှုကို လိုက်နာပါက၊ ထို့နောက် X = k အောင်မြင်မှုဖြစ်နိုင်ခြေကို အောက်ပါဖော်မြူလာဖြင့် ရှာတွေ့နိုင်သည်-

P(X=k) = λ ^k * e ^{– λ} / k!

ရွှေ-

• λ: တိကျသောကြားကာလတစ်ခုအတွင်း ဖြစ်ပေါ်သည့် ပျမ်းမျှအောင်မြင်မှုအရေအတွက်
• k: အောင်မြင်မှုအရေအတွက်
• e- ခန့်မှန်းခြေအားဖြင့် 2.71828 နှင့်ညီမျှသော ကိန်းသေတစ်ခု

ဥပမာအားဖြင့်၊ ဆေးရုံတစ်ခုသည် တစ်နာရီလျှင် ပျမ်းမျှ မွေးဖွားမှု ၂ ခု ခံစားရသည်ဆိုပါစို့။ 0၊ 1၊ 2၊ 3 မွေးဖွားမှု စသည်ဖြင့် တွေ့ကြုံရနိုင်ခြေကို ဆုံးဖြတ်ရန် အထက်ဖော်ပြပါ ဖော်မြူလာကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။ သတ်မှတ်နာရီအတွင်း

P(X=0) = 2 ⁰ * e ^{– 2} / 0! = 0.1353

P(X=1) = 2 ¹ * e ^{– 2/1} ! = 0.2707

P(X=2) = 2 ² * e ^{– 2/2} ! = 0.2707

P(X=3) = 2 ³ * e ^{– 2/3} ! = 0.1805

ကျွန်ုပ်တို့သည် အဆုံးမရှိအထိ မွေးဖွားနိုင်သည့် အရေအတွက် ဖြစ်နိုင်ခြေကို တွက်ချက်နိုင်သည်။ ထို့နောက် ဤဖြစ်နိုင်ချေ ဖြန့်ဖြူးမှုကို မြင်သာစေရန် ရိုးရှင်းသော histogram တစ်ခုကို ဖန်တီးသည်-

တိုးပွားလာသော Poisson ဖြစ်နိုင်ခြေများကို တွက်ချက်ခြင်း။

အထက်ပါဖော်မြူလာကို အသုံးပြု၍ Poisson ဖြစ်နိုင်ခြေတစ်ခုတည်း (ဥပမာ- ဆေးရုံတစ်ရုံတွင် ကလေးမွေးဖွားမှုဖြစ်နိုင်ခြေ) ကို အထက်ဖော်ပြပါဖော်မြူလာကို အသုံးပြု၍ တွက်ချက်ရန် ရိုးရှင်းသော်လည်း တိုးပွားလာသော Poisson ဖြစ်နိုင်ခြေများကို တွက်ချက်ရန်အတွက် တစ်ဦးချင်းဖြစ်နိုင်ချေများကို ပေါင်းထည့်ရန် လိုအပ်ပါသည်။

ဥပမာအားဖြင့်၊ သတ်မှတ်နာရီအတွင်း ဆေးရုံမှ မွေးဖွားမှု 1 သို့မဟုတ် ယင်းထက်နည်းသော ကလေးမွေးဖွားနိုင်ခြေကို ကျွန်ုပ်တို့ သိလိုသည်ဆိုကြပါစို့။ ဤဖြစ်နိုင်ခြေကို တွက်ချက်ရန် အောက်ပါဖော်မြူလာကို ကျွန်ုပ်တို့ အသုံးပြုပါမည်။

P(X≤1) = P(X=0) + P(X=1) = 0.1353 + 0.2707 = 0.406

ဖြစ်နိုင်ခြေများစွာကို ပေါင်းထည့်ခြင်းတို့ ပါဝင်သောကြောင့် ၎င်းကို စုဆောင်းဖြစ်နိုင်ခြေ ဟု ခေါ်သည်။ အလားတူဖော်မြူလာကို အသုံးပြု၍ ပေးထားသောနာရီတစ်ခုအတွင်း k သို့မဟုတ် နည်းပါးသော ကလေးမွေးဖွားမှုကြုံတွေ့ရနိုင်ခြေကို တွက်ချက်နိုင်သည်-

P(X≤0) = P(X=0) = 0.1353

P(X≤1) = P(X=0) + P(X=1) = 0.1353 + 0.2707 = 0.406

P(X≤2) = P(X=0) + P(X=1) + P(X=2) =0.1353 + 0.2707 + 0.2707 = 0.6767

ကျွန်ုပ်တို့သည် အဆုံးမရှိသည့်အထိ မွေးဖွားမှုအရေအတွက်အတွက် ဤတိုးပွားလာနိုင်သည့် ဖြစ်နိုင်ခြေများကို တွက်ချက်နိုင်သည်။ ထို့နောက် ဤစုပြုံဖြစ်နိုင်ခြေဖြန့်ဝေမှုကို မြင်သာစေရန် ဟစ်စတိုဂရမ်တစ်ခုကို ဖန်တီးနိုင်သည်-

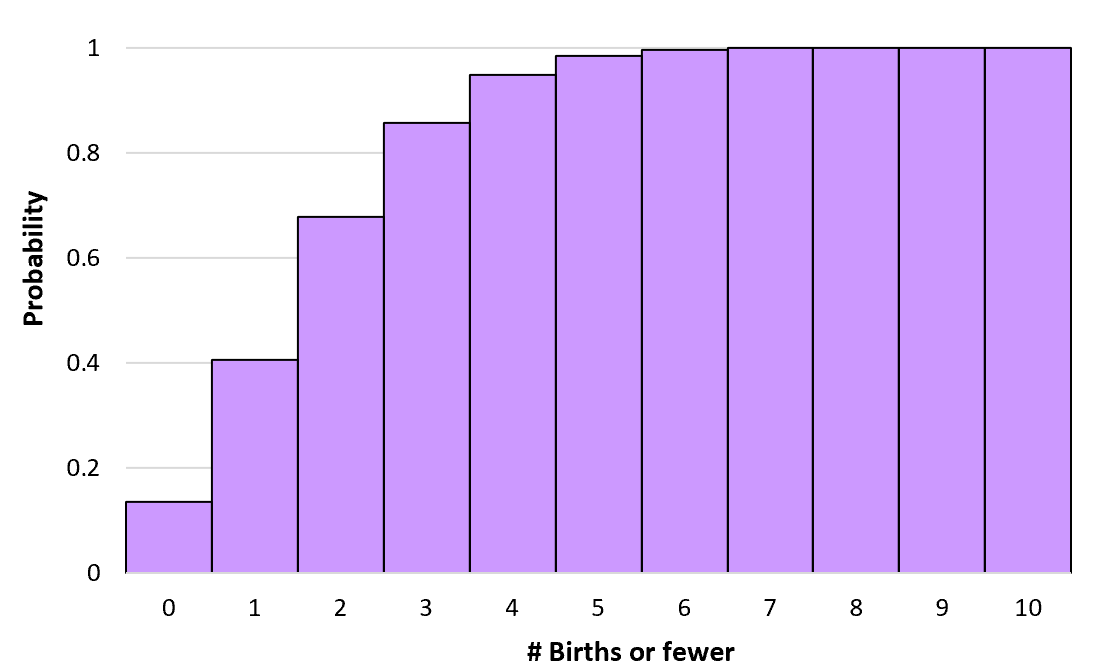
Poisson ဖြန့်ဖြူးခြင်း၏ ဂုဏ်သတ္တိများ

Poisson ဖြန့်ဖြူးမှုတွင် အောက်ပါဂုဏ်သတ္တိများ ရှိသည်။

ဖြန့်ဖြူးမှု၏ပျမ်းမျှမှာ λ ဖြစ်သည်။

ဖြန့်ဖြူးခြင်း၏ကွဲလွဲမှုသည် λ လည်းဖြစ်သည်။

ဖြန့်ဖြူးမှု၏စံသွေဖည်မှုမှာ √ λ ဖြစ်သည်။

ဥပမာအားဖြင့်၊ ဆေးရုံတစ်နာရီလျှင် ပျမ်းမျှ ၂ ယောက်မွေးသည်ဆိုပါစို့။

ပေးထားသည့်နာရီတစ်ခုအတွင်း မျှော်မှန်းထားသော ပျမ်းမျှမွေးဖွားမှုအရေအတွက်မှာ λ = 2 မွေးဖွားသည်။

ကျွန်ုပ်တို့မျှော်လင့်ထားသော မွေးဖွားမှုအရေအတွက် ကွာခြားချက်မှာ λ = 2 မွေးဖွားခြင်း ဖြစ်သည်။

ငါးဖြန့်ဖြူးရေး လက်တွေ့ပြဿနာ

Poisson ဖြန့်ဖြူးမှုဆိုင်ရာ သင်၏အသိပညာကို စမ်းသပ်ရန် အောက်ပါအလေ့အကျင့်ပြဿနာများကို အသုံးပြုပါ။

မှတ်ချက်- ဤမေးခွန်းများအတွက် အဖြေများကို တွက်ချက်ရန် Poisson ဖြန့်ချီရေးဂဏန်းတွက်စက်ကို ကျွန်ုပ်တို့ အသုံးပြုပါမည်။

ပြဿနာ ၁

မေးခွန်း- အချို့သောဝဘ်ဆိုဒ်တစ်ခုသည် တစ်နာရီလျှင် 10 ရောင်းရကြောင်း ကျွန်ုပ်တို့သိပါသည်။ ပေးထားသည့်နာရီအတွင်း၊ site သည် 8 ခုတိတိအရောင်းအ၀ယ်ပြုလုပ်နိုင်ခြေအဘယ်နည်း။

အဖြေ- λ = 10 နှင့် x = 8 ပါသော Poisson ဖြန့်ချီရေးဂဏန်းတွက်စက်ကို အသုံးပြု၍ P(X=8) = 0.1126 ကို တွေ့ရှိရသည်။

ပြဿနာ ၂

မေးခွန်း- အချို့သောအိမ်ခြံမြေအေးဂျင့်တစ်ဦးသည် တစ်လလျှင် ပျမ်းမျှ 5 ရောင်းရကြောင်း ကျွန်ုပ်တို့သိပါသည်။ ပေးထားသည့်လတွင်၊ သူမသည် ရောင်းအား 7 ခုထက်ပို၍ ဖြစ်နိုင်ခြေအဘယ်နည်း။

အဖြေ- λ = 5 နှင့် x = 7 ပါသော Poisson ဖြန့်ချီရေးဂဏန်းတွက်စက်ကို အသုံးပြု၍ P(X>7) = 0.13337 ကို ကျွန်ုပ်တို့တွေ့ရှိသည်။

ပြဿနာ ၃

မေးခွန်း- အချို့သောဆေးရုံတစ်ခုသည် တစ်နာရီလျှင် ပို့ဆောင်မှု 4 ခု ကြုံတွေ့ရကြောင်း ကျွန်ုပ်တို့သိပါသည်။ ပေးထားသည့်နာရီတစ်ခုတွင် မွေးဖွားမှု 4 ခု သို့မဟုတ် အနည်းငယ်သာရှိနိုင်ခြေ မည်မျှရှိသနည်း။

အဖြေ- λ = 4 နှင့် x = 4 ပါသော Poisson ဖြန့်ချီရေးဂဏန်းတွက်စက်ကို အသုံးပြု၍ P(X≤4) = 0.62884 ကို ကျွန်ုပ်တို့တွေ့ရှိသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ ဆောင်းပါးများသည် မတူညီသော စာရင်းအင်းဆော့ဖ်ဝဲများတွင် Poisson ဖြန့်ဖြူးမှုကို အသုံးပြုပုံကို ရှင်းပြသည်-

R တွင် Poisson ဖြန့်ဖြူးမှုကိုအသုံးပြုနည်း
Excel တွင် Poisson distribution ကိုအသုံးပြုနည်း
TI-84 ဂဏန်းတွက်စက်တွင် Poisson Probabilities တွက်ချက်နည်း
Poisson ဖြန့်ဖြူးခြင်း၏ လက်တွေ့ကမ္ဘာ ဥပမာများ
ငါးဖြန့်ဝေဂဏန်းတွက်စက်