Socs- ဖြန့်ဖြူးမှုများကို ဖော်ပြရန် အသုံးဝင်သော အတိုကောက်

စာရင်းဇယားများတွင်၊ ကျွန်ုပ်တို့သည် ဒေတာအစုတစ်ခုအား မည်သို့ဖြန့်ဝေကြောင်းကို မကြာခဏ နားလည်လိုကြသည်။ အထူးသဖြင့်၊ ဖြန့်ဖြူးမှုနှင့်ပတ်သက်၍ သိရန် အသုံးဝင်သည့်အချက်လေးချက်ရှိသည်။

၁ ။ ပုံသဏ္ဍာန်

• ဖြန့်ချီမှုသည် အချိုးညီညီ သို့မဟုတ် တစ်ဖက်သို့ စောင်းနေပါသလား။
• ဖြန့်ဖြူးမှုသည် unimodal (one peak) သို့မဟုတ် bimodal ( two peaks) လား။

2. Outliers

• ဖြန့်ဖြူးမှုတွင် အစွန်းအထင်းများ ရှိပါသလား။

3. စင်တာ

• ဆိုလိုရင်း၊ ပျမ်းမျှနှင့် ဖြန့်ဖြူးမှုပုံစံက ဘာလဲ?

4.Spread

• အကွာအဝေး၊ interquartile အကွာအဝေး၊ စံသွေဖည်မှုနှင့် ဖြန့်ဖြူးမှုကွဲလွဲမှုတို့သည် အဘယ်နည်း။

SOCS သည် ဤအချက်လေးချက်ကို မှတ်သားရန် အသုံးဝင်သော အတိုကောက်ဖြစ်သည်။ ၎င်းသည် “ ပုံသဏ္ဍာန်၊ အစွန်းအထင်း၊ အလယ်၊ ပြန့်ပွားခြင်း” ကိုဆိုလိုသည်။

ဖြန့်ဖြူးမှုကိုဖော်ပြရန် SOCS ကိုအသုံးပြုပုံ၏ ရိုးရှင်းသောဥပမာတစ်ခုကို ဖြတ်သန်းကြည့်ကြပါစို့။

ဥပမာ- ဖြန့်ဖြူးမှုကိုဖော်ပြရန် SOCS ကိုအသုံးပြုနည်း

မတူညီသောအပင် 20 ၏အမြင့်နမူနာကိုပြသသည့်အောက်ပါဒေတာအစုံရှိသည်ဆိုကြပါစို့။

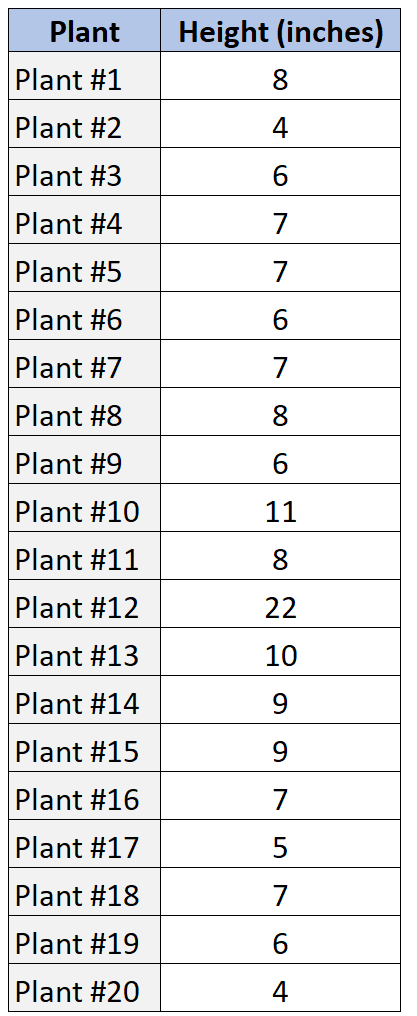
ဤဒေတာဖြန့်ဝေမှုတန်ဖိုးများကိုဖော်ပြရန် SOCS ကို ကျွန်ုပ်တို့အသုံးပြုပုံမှာ ဤအရာဖြစ်သည်။

ပုံသဏ္ဍာန်

ပထမဦးစွာ ကျွန်ုပ်တို့သည် ဖြန့်ဖြူးမှုပုံစံကို ဖော်ပြလိုပါသည်။

ဖြန့်ဖြူးမှု၏ပုံသဏ္ဍာန်ကို မြင်ယောင်မြင်ယောင်ရန် အသုံးဝင်သောနည်းလမ်းမှာ ဒေတာအစုအတွင်း တန်ဖိုးတစ်ခုစီ၏ ကြိမ်နှုန်းများကိုပြသသည့် ဟီစတိုဂရမ်တစ်ခုကို ဖန်တီးရန်ဖြစ်သည်-

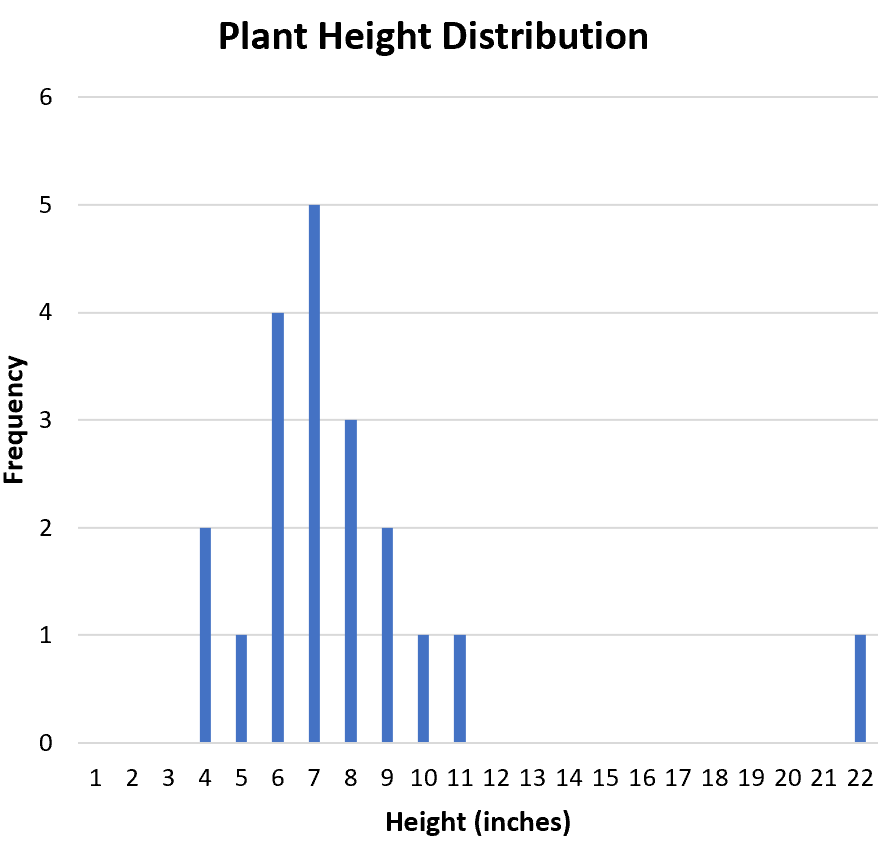
ဖြန့်ချီမှုသည် အချိုးညီညီ သို့မဟုတ် တစ်ဖက်သို့ စောင်းနေပါသလား။   ဟစ်စတိုဂရမ်မှ ဖြန့်ချီမှုသည် ခန့်မှန်းခြေ အချိုးကျကြောင်း ကျွန်ုပ်တို့ မြင်နိုင်သည်။ တစ်နည်းဆိုရသော် တန်ဖိုးများသည် တစ်နည်းမဟုတ် တစ်နည်း ဘက်လိုက်သည်မဟုတ်။

ဖြန့်ဖြူးမှုသည် unimodal (one peak) သို့မဟုတ် bimodal ( two peaks) လား။ ဖြန့်ဖြူးမှုသည် ပုံမှန်မဟုတ်ပေ။ တန်ဖိုး “ 7” တွင် အထွတ်အထိပ်ရှိသည်။

အစွန်းအထင်းများ

ထို့နောက်၊ ဒေတာအတွဲတွင် အစွန်းအထင်းများ ရှိမရှိ ဆုံးဖြတ်လိုပါသည်။ ဟစ်စတိုဂရမ်မှ ကျွန်ုပ်တို့သည် ဖြန့်ဖြူးမှုကို အမြင်အာရုံစစ်ဆေးနိုင်ပြီး 22 သည် သာလွန်နိုင်ချေရှိသည်ကို တွေ့နိုင်သည်-

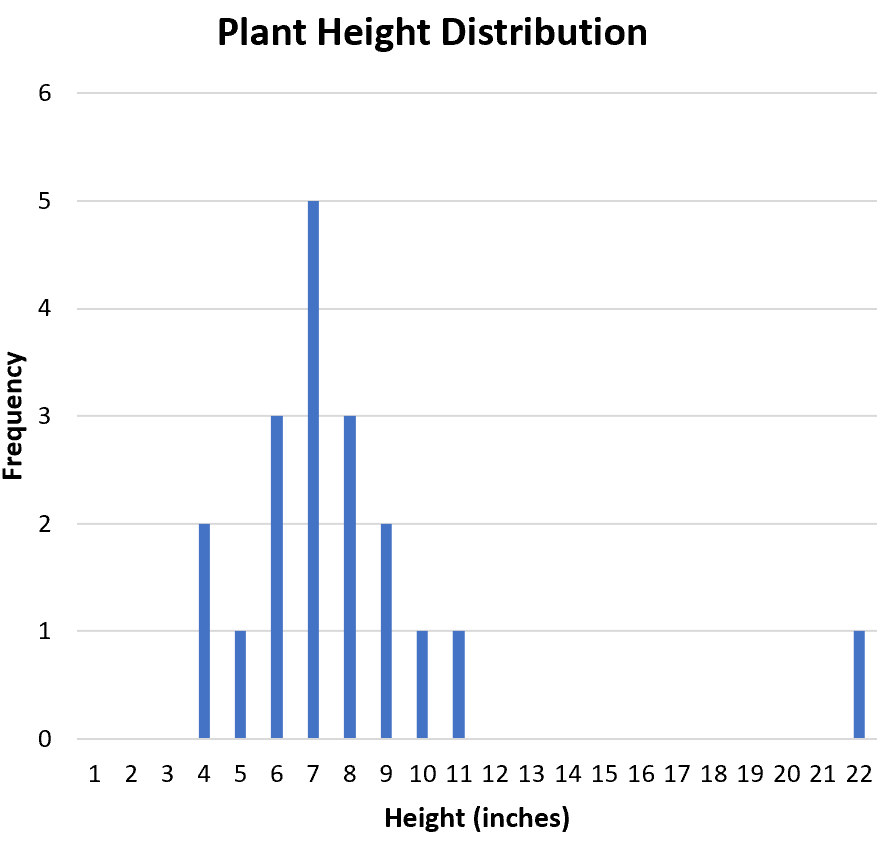
outlier ကို တရားဝင်သတ်မှတ်ရန် ဘုံနည်းလမ်းမှာ တတိယ quartile အထက် သို့မဟုတ် ပထမ quartile အောက်ရှိ ကြားခံအကွာအဝေး၏ 1.5 ဆရှိသော မည်သည့်တန်ဖိုးမဆိုဖြစ်သည်။

interquartile အကွာအဝေးဂဏန်းတွက်စက်ကို အသုံးပြု၍ ကုန်ကြမ်းဒေတာတန်ဖိုး 20 ကို ထည့်သွင်းနိုင်ပြီး တတိယ quartile သည် 9 ဖြစ်ပြီး interquartile အကွာအဝေးသည် 3 ဖြစ်ပြီး ထို့ကြောင့် 9 + (1.5*3) = 13.5 ထက်ကြီးသောတန်ဖိုးသည် သာလွန်ကြောင်းတွေ့ရပါသည်။ အဓိပ္ပါယ်။

22 သည် 13.5 ထက် ကြီးသောကြောင့် 22 ကို အစွန်းထွက်အဖြစ် ကြေညာနိုင်ပါသည်။

စင်တာ

ထို့နောက် ဖြန့်ဖြူးမှု၏ဗဟိုတည်နေရာကို ဖော်ပြလိုပါသည်။ ကျွန်ုပ်တို့သုံးနိုင်သော ဗဟိုသဘောထား၏ ဘုံအတိုင်းအတာ သုံးရပ်မှာ ပျမ်းမျှ၊ အလယ်အလတ်နှင့် မုဒ်ဖြစ်သည်။

ဆိုလိုရင်း- ဤသည်မှာ ဖြန့်ဖြူးမှု၏ ပျမ်းမျှတန်ဖိုးဖြစ်သည်။ တစ်ခုချင်းတန်ဖိုးများအားလုံးကို ပေါင်းထည့်ပြီးနောက် စုစုပေါင်းတန်ဖိုးအရေအတွက်ဖြင့် ပိုင်းခြားခြင်းဖြင့် ၎င်းကို ကျွန်ုပ်တို့တွေ့ရှိသည်-

ပျမ်းမျှ = (8+4+6+7+7+6+7+8+6+11+8+22+10+9+9+7+5+7+6+4) / 20 = 7.85

အလယ်အလတ်- ဤသည်မှာ ဖြန့်ဖြူးမှု၏ “ ပျမ်းမျှ” တန်ဖိုးဖြစ်သည်။ အသေးဆုံးမှ အကြီးဆုံးတန်ဖိုးများအားလုံးကို စီစဥ်ပြီး အလယ်တန်းတန်ဖိုးကို ခွဲခြားသတ်မှတ်ခြင်းဖြင့် ၎င်းကို ကျွန်ုပ်တို့တွေ့ရှိသည်။ 7 ဖြစ်သွားပါတယ်။

4၊ 4၊ 5၊ 6၊ 6၊ 6၊ 6၊ 7၊ 7၊ 7၊ 7၊ 7၊ 8၊ 8၊ 8၊ 9၊ 9၊ 10၊ 11၊ 22

မုဒ်- ဤသည်မှာ မကြာခဏပေါ်လာသော တန်ဖိုးဖြစ်သည်။ 7 ဖြစ်သွားပါတယ်။

ကူးစက်ပျံ့နှံ့သည်

ဆက်လက်၍ ကျွန်ုပ်တို့သည် ဖြန့်ဖြူးမှုတွင် တန်ဖိုးများကို ဖော်ပြလိုပါသည်။ ကျွန်ုပ်တို့သုံးနိုင်သော ပြန့်ကျဲမှု၏ ဘုံအတိုင်းအတာလေးခုမှာ အကွာအဝေး၊ interquarile အကွာအဝေး၊ စံသွေဖည်မှုနှင့် ကွဲပြားမှုဖြစ်သည်။

အပိုင်းအခြား- ၎င်းသည် ဒေတာအတွဲတွင် အကြီးဆုံးနှင့် အသေးငယ်ဆုံးတန်ဖိုးအကြား ကွာခြားချက်ဖြစ်သည်။ ဒါက 22 – 4 = 18 ဖြစ်သွားပါတယ်။

Interquartile Range- ဒေတာတန်ဖိုးများ၏ အလယ် 50% ၏ အကျယ်ကို တိုင်းတာသည်။ interquartile range calculator တွင် ဒေတာကုန်ကြမ်းတန်ဖိုး 20 ကို ထည့်သွင်းခြင်းဖြင့် ၎င်းသည် 3 နှင့် ညီမျှကြောင်း ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။

စံသွေဖည်မှု- ဤသည်မှာ ဒေတာတန်ဖိုးများ၏ ပျမ်းမျှဖြန့်ဖြူးမှုအတိုင်းအတာတစ်ခုဖြစ်သည်။ ကွဲလွဲမှုနှင့် စံသွေဖည်မှုဂဏန်းတွက်စက်ထဲသို့ ဒေတာအကြမ်း 20 တန်ဖိုးများကို ထည့်သွင်းခြင်းဖြင့် စံသွေဖည်မှုသည် 3.69 နှင့် ညီမျှကြောင်း ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။

ကွဲလွဲမှု- ဤသည်မှာ ရိုးရိုးစံသွေဖည်မှု၊ နှစ်ထပ်ကိန်းဖြစ်သည်။ ၎င်းသည် 3.69 ² = 13.63 နှင့် ညီမျှသည်။

နိဂုံး

SOCS ကို လမ်းညွှန်အဖြစ် အသုံးပြု၍ အပင်အမြင့်ဖြန့်ဖြူးမှုကို အောက်ပါအတိုင်း ဖော်ပြနိုင်ခဲ့ပါသည်။

• ဖြန့်ဖြူးမှုသည် စံမညီဘဲ အချိုးကျသောကြောင့် ၎င်းတွင် အထွတ်အထိပ်တစ်ခုသာရှိ၍ တစ်ဖက် သို့မဟုတ် အခြားတစ်ဖက်သို့ လှည့်၍မရပေ။
• ဖြန့်ဖြူးမှုတွင် အကြမ်းဖျင်းတစ်ခုရှိသည်- 22။
• ဖြန့်ဖြူးမှုတွင် ပျမ်းမျှ 7.85၊ ပျမ်းမျှ 7 နှင့် 7 မုဒ်ရှိသည်။
• ဖြန့်ဖြူးမှုတွင် အပိုင်းအခြား 18၊ ကွာတားအကွာအဝေး 3၊ စံသွေဖည်မှု 3.69 နှင့် ကွဲလွဲမှု 13.63 ရှိသည်။

ဖြန့်ချီမှု၏ပုံသဏ္ဍာန်၊ အစွန်းအထင်းရှိမရှိ၊ အနီးစပ်ဆုံးအချက်အချာကျသည့်နေရာ၊ ဒေတာတန်ဖိုးများကို မည်သို့ဖြန့်ဝေရမည်ကို အပြည့်အဝနားလည်ရန် SOCS ကို အသုံးပြုနိုင်ကြောင်း သတိပြုပါ။ ဖြစ်ကြပါသည်။