အဆင့် (စာရင်းအင်း)

ဤဆောင်းပါး၌ ကျွန်ုပ်တို့သည် ကိန်းဂဏာန်းစာရင်းဇယားတွင် မည်သည့်အတိုင်းအတာနှင့် ၎င်းကို တွက်ချက်ပုံကို ရှင်းပြထားသည်။ ဒေတာအတွဲ၏ နယ်ပယ်တွင် ဖြေရှင်းနိုင်သော လေ့ကျင့်ခန်းတစ်ခုကို သင်တွေ့လိမ့်မည်ဖြစ်ပြီး၊ နောက်ဆုံးတွင် ၎င်းကို မည်သည့်အတွက်နှင့် အသုံးပြုသင့်သည်ကို သင့်အား ပြသပါမည်။

ကိန်းဂဏန်းစာရင်းအင်းများတွင် အပိုင်းအခြားသည် အဘယ်နည်း။

စာရင်းဇယားများတွင်၊ အကွာအဝေးသည် နမူနာဒေတာ၏ အများဆုံးတန်ဖိုးနှင့် အနိမ့်ဆုံးတန်ဖိုးအကြား ကွာခြားချက်ကို ညွှန်ပြသော ပြန့်ကျဲမှုအတိုင်းအတာတစ်ခုဖြစ်သည်။ ထို့ကြောင့်၊ လူဦးရေ သို့မဟုတ် စာရင်းအင်းနမူနာ၏အတိုင်းအတာကို တွက်ချက်ရန်၊ အများဆုံးတန်ဖိုးကို အနိမ့်ဆုံးတန်ဖိုးမှ နုတ်ရပါမည်။

ဥပမာအားဖြင့်၊ ဒေတာအတွဲတစ်ခု၏ အမြင့်ဆုံးတန်ဖိုးမှာ 9 ဖြစ်ပြီး အနိမ့်ဆုံးတန်ဖိုးမှာ 2 ဖြစ်ပါက၊ ဤစာရင်းအင်းနမူနာ၏ အပိုင်းအခြားသည် 7 (9-2=7) ဖြစ်သည်။

ကိန်းဂဏန်းအကွာအဝေးကို အတိုင်းအတာ သို့မဟုတ် အတိုင်းအတာအတိုင်းအတာဟုလည်း ခေါ်သည်။

ထို့ကြောင့်၊ range သည် ကွဲလွဲမှု၊ စံသွေဖည်မှု (သို့မဟုတ် စံသွေဖည်မှု)၊ ပျမ်းမျှသွေဖည်မှုနှင့် ကွဲလွဲမှု၏ကိန်းဂဏန်းများနှင့်အတူ ကွဲလွဲမှု၏အတိုင်းအတာတစ်ခုဖြစ်သည်။

ကိန်းဂဏန်းစာရင်းဇယားတွင် အပိုင်းအခြားကို မည်ကဲ့သို့ တွက်ချက်မည်နည်း။

နမူနာတစ်ခု၏ အကွာအဝေးကို ကိန်းဂဏန်းနမူနာဒေတာ၏ လွန်ကဲသောတန်ဖိုးများကို နုတ်ခြင်းဖြင့် တွက်ချက်သည်၊ ဆိုလိုသည်မှာ နမူနာတစ်ခု၏အကွာအဝေးသည် ဒေတာအားလုံး၏အမြင့်ဆုံးတန်ဖိုးနှင့် အနိမ့်ဆုံးတန်ဖိုးကို အနှုတ်လက္ခဏာဖြင့် တွက်ချက်သည်။

ထို့ကြောင့် ဒေတာအစုတစ်ခု၏ ကိန်းဂဏန်းအကွာအဝေးကို တွက်ချက်ရန်အတွက် ဖော်မြူလာမှာ-

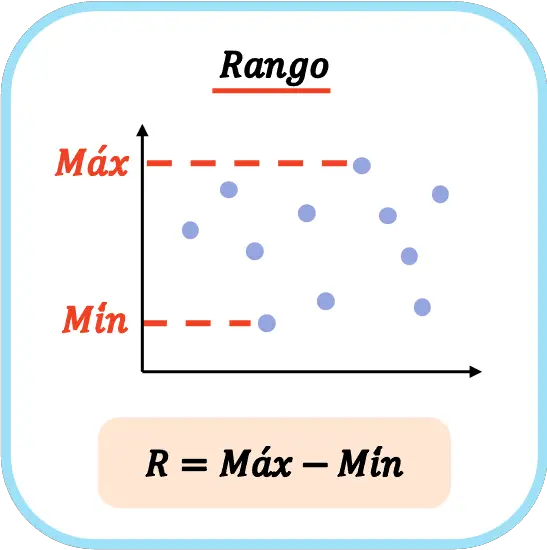
စာရင်းဇယားများတွင်၊ အရင်းအနှီး R အတွက် သင်္ကေတကို ဒေတာစီးရီးတစ်ခု၏အတိုင်းအတာကို ဖော်ပြရန် မကြာခဏအသုံးပြုသည်။

လွန်ကဲသောတန်ဖိုးများအကြား ကွာခြားချက်ကို သင်ဆုံးဖြတ်ရန်သာ လိုအပ်သောကြောင့် ဒေတာအစုတစ်ခု၏ အကွာအဝေးကို တွက်ချက်ခြင်းသည် အလွန်ရိုးရှင်းပါသည်။ သင်ဂရုပြုရမည့်တစ်ခုတည်းသောအရာမှာ အမြင့်ဆုံးနှင့် အနိမ့်ဆုံးဒေတာကို မှန်မှန်ကန်ကန်ရယူပြီး မည်သည့်နံပါတ်ကိုမဆို မေ့လျော့ခြင်းပင်ဖြစ်သည်။

ဥပမာ အပိုင်းအခြား (ကိန်းဂဏန်း)

ကိန်းဂဏန်းစာရင်းဇယားတွင် အပိုင်းအခြား၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်အား မြင်ပြီးနောက်၊ အောက်တွင် အလုပ်လုပ်သော ဥပမာတစ်ခုဖြစ်ပြီး ဒေတာအတွဲတစ်ခု၏ အကွာအဝေးကို မည်သို့ရယူထားသည်ကို သင်ကြည့်ရှုနိုင်ပါသည်။

• ကုမ္ပဏီတစ်ခုသည် ပြီးခဲ့သော အနှစ်နှစ်ဆယ်အတွင်း ၎င်း၏ ထင်ရှားကျော်ကြားသော ထုတ်ကုန်မှရရှိသော ရောင်းအားကို ကိန်းဂဏန်းအရ ပိုင်းခြားစိတ်ဖြာလိုပါသည်။ ဒီလိုလုပ်ဖို့၊ အဆင့်သတ်မှတ်ခြင်းအပါအဝင် ကိန်းဂဏန်းအစီအမံများစွာကို တွက်ချက်ခိုင်းပါတယ်။ ထုတ်ကုန်၏ရောင်းအားသည် အောက်ပါဇယားတွင်ပြထားသည့်အတိုင်းဖြစ်ပါက၊ ဤဒေတာအစုံ၏အတိုင်းအတာသည် အဘယ်နည်း။

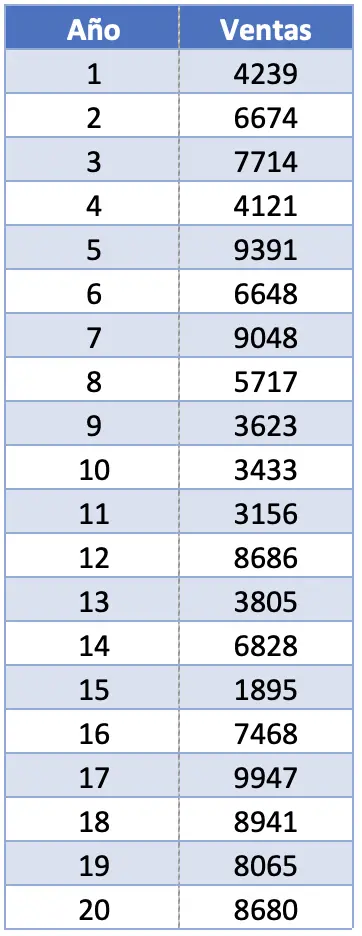
ဤလေ့ကျင့်ခန်းတွင် ကျွန်ုပ်တို့တွင် လေ့လာတွေ့ရှိချက် 20 ရှိသည်။ အမှန်တကယ်တွင်၊ ကျွန်ုပ်တို့သည် အကြီးဆုံးတန်ဖိုးနှင့် အသေးငယ်ဆုံးတန်ဖိုးကိုသာ စိတ်ဝင်စားသောကြောင့် နမူနာတစ်ခု၏အတိုင်းအတာကို တွက်ချက်ရာတွင် စူးစမ်းမှုစုစုပေါင်းအရေအတွက်သည် ကွာခြားမှုမရှိပါ။

ထို့ကြောင့် ဤစာရင်းအင်းနမူနာ၏အတိုင်းအတာကိုရှာဖွေရန် အထက်တွင်ဖော်ပြထားသော ဖော်မြူလာကို အသုံးပြုရပါမည်။

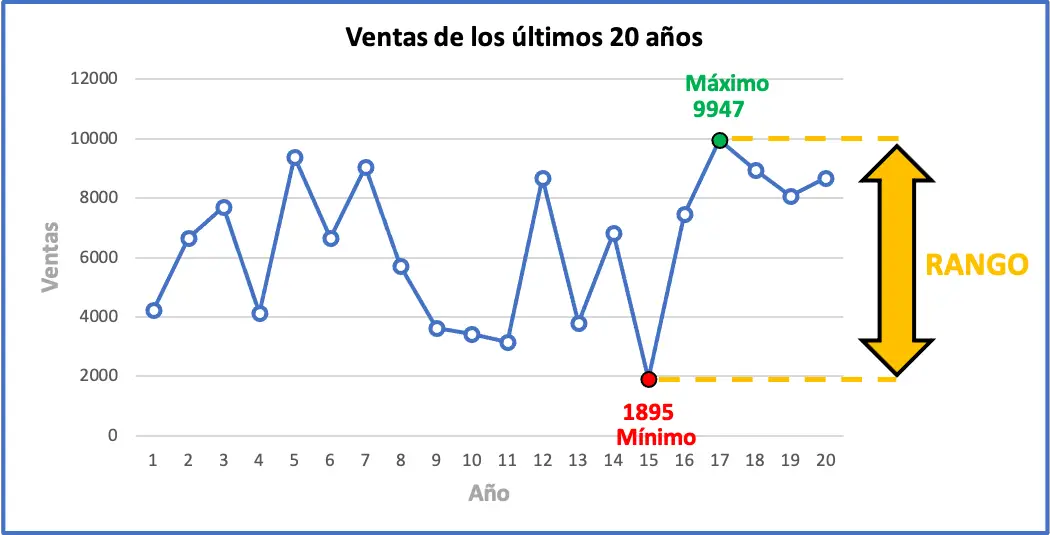
ကြားကာလ၏အမြင့်ဆုံးတန်ဖိုးမှာ 9947 ယူနစ်ရောင်းချရပြီး အနိမ့်ဆုံးတန်ဖိုးမှာ 1895 ဖြစ်သည်။ ထို့ကြောင့်၊ ဒေတာအတွဲ၏အကွာအဝေးကိုရှာဖွေရန် ဤတန်ဖိုးနှစ်ခုကို နုတ်ရန် လိုအပ်သည်-

ဆိုလိုသည်မှာ လွန်ခဲ့သည့် နှစ်အနည်းငယ်အတွင်း အရောင်းရဆုံးပြောင်းလဲမှုမှာ 8,052 ယူနစ်ဖြစ်သည်။ အောက်တွင် ၎င်း၏ ကိန်းဂဏန်းအကွာအဝေးနှင့်အတူ လေ့ကျင့်ခန်းဒေတာအားလုံးကို ဂရပ်ဖစ်ဖြင့် မြင်နိုင်သည်၊ ဂရပ်ဖစ်သည် သင့်အား အပိုင်းအခြား၏ အဓိပ္ပါယ်ကို နားလည်ရန် ကူညီပေးပေမည်။

ကိန်းဂဏန်းအကွာအဝေးကို ဘာအတွက်သုံးသလဲ။

စာရင်းအင်းဆိုင်ရာ အတိုင်းအတာ၏ သဘောတရားကို နားလည်ရန် အပြီးသတ်ရန်၊ ၎င်းကို အဘယ်အရာအတွက် အသုံးပြုပြီး ဤပြန့်ပွားမှု၏ အတိုင်းအတာကို အဓိပ္ပာယ်ဖွင့်ဆိုရမည်ကို ကျွန်ုပ်တို့ မြင်တွေ့ရမည်ဖြစ်သည်။

စာရင်းဇယားများတွင်၊ အပိုင်းအခြားသည် ဒေတာအစုတစ်ခု၏ အများဆုံးတန်ဖိုးနှင့် အနိမ့်ဆုံးတန်ဖိုးအကြား ကွာခြားချက်ကို ပြသည်။ ထို့ကြောင့်၊ အကွာအဝေးသည် ဒေတာအစုတစ်ခု၏ စုစုပေါင်းပျံ့နှံ့မှုကို ညွှန်ပြရန်အတွက် အသုံးပြုသည့် အတိုင်းအတာတစ်ခုဖြစ်သည် ။

ဒေတာအစုတစ်ခု၏ အကွာအဝေးတန်ဖိုးကို သိသောအခါ၊ ထိုအစုရှိ စူးစမ်းလေ့လာမှုနှစ်ခုကြားတွင် အမြင့်ဆုံးခြားနားချက်ကို သင်သိနိုင်ပြီး၊ ထို့ကြောင့် ဒေတာသည် ပြန့်ကျဲနေသလား သို့မဟုတ် နီးကပ်မှုရှိမရှိ စိတ်ကူးတစ်ခုရနိုင်သည်။ ယေဘူယျအားဖြင့်၊ အကွာအဝေးကို တတ်နိုင်သမျှ အနည်းဆုံးဖြစ်အောင် ပြုလုပ်ခြင်းသည် အားသာချက်ဖြစ်သည်၊ အကြောင်းမှာ ၎င်းသည် ကွဲလွဲမှုအနည်းငယ်သာရှိသောကြောင့် တွက်ချက်မှုများ ပိုမိုတိကျလာမည်ဖြစ်သည်။

ဥပမာအားဖြင့်၊ အကွာအဝေးသည် မတူညီသောနမူနာနှစ်ခုကြား နှိုင်းယှဉ်မှုကို ခွင့်ပြုနိုင်သည့် တိုင်းတာမှုတစ်ခု ဖြစ်နိုင်သည်၊ အကြောင်းမှာ ၎င်းသည် နမူနာများ၏ ကွဲလွဲမှုများကို စိတ်ကူးတစ်ခုရနိုင်စေသောကြောင့် ဖြစ်သည်။

သို့ရာတွင်၊ ၎င်းသည် လွဲမှားစေနိုင်သောကြောင့် ကိန်းဂဏန်းအကွာအဝေးကို ဘာသာပြန်ရာတွင် သတိထားသင့်သည်။ ဒေတာအတွဲတစ်ခုတွင် အမှန်တကယ်ပျံ့နှံ့မှု အလွန်နည်းသောကြောင့် ဖြစ်နိုင်သည်၊ သို့သော် နမူနာအတွင်း အစွန်းထွက် တစ်ခုရှိနေပါက၊ အကွာအဝေးသည် အလွန်ကျယ်ပြန့်မည်ဖြစ်ပြီး ထို့ကြောင့် နမူနာ၏ပျံ့နှံ့မှုကို ကောင်းစွာထင်ဟပ်မည်မဟုတ်ပါ။

ထို့အပြင်၊ တန်ဖိုးများသည် ဆယ်ဂဏန်း၏ အစီအစဥ်ဖြစ်သော 5 အဆင့်ရှိနမူနာတစ်ခုအတွက် တန်ဖိုးများသည် တူညီသောအဆင့်ရှိရန် ထောင်ပေါင်းများစွာ၏တန်ဖိုးရှိသော နမူနာတစ်ခုအနေဖြင့် ၎င်းသည် တူညီသည်မဟုတ်ပါ။ ယုတ္တိဗေဒအရ၊ အပိုင်းအခြားနှစ်ခုစလုံးတွင် တူညီသောနံပါတ်ရှိလျှင်ပင်၊ ပထမနမူနာသည် ဒုတိယထက် များစွာပို၍ကွဲပြားပါသည်။

နိဂုံးချုပ်အနေနှင့်၊ အပိုင်းအခြားသည် ဒေတာအစုတစ်ခု၏ ပျံ့နှံ့မှုကို ခွဲခြမ်းစိတ်ဖြာရန်အတွက် အသုံးဝင်သော ကိန်းဂဏန်းတိုင်းတာမှုတစ်ခုဖြစ်သော်လည်း ဒေတာကို မှန်ကန်စွာအနက်ပြန်ဆိုရန်၊ အခြားမက်ထရစ်များကိုလည်း တွက်ချက်ရမည်ဖြစ်သည်။