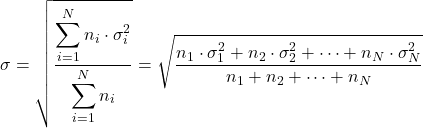စံသွေဖည်မှု (သို့မဟုတ် စံသွေဖည်မှု)
ဤဆောင်းပါးတွင် စံသွေဖည်ခြင်း (Standard Deviation) ဟူသည် မည်သည်ကို ရှင်းပြထားသည်။ စံသွေဖည်မှုကို တွက်ချက်နည်း၊ ဒေတာနမူနာ၏ စံသွေဖည်မှုကို ရှာဖွေရန် အဆင့်ဆင့် လက်တွေ့နမူနာနှင့် အွန်လိုင်းဂဏန်းတွက်စက်ကို သင်လေ့လာနိုင်မည်ဖြစ်သည်။
စံသွေဖည်မှု (သို့မဟုတ် စံသွေဖည်မှု) ဟူသည် အဘယ်နည်း။
စံသွေဖည်မှု ၊ စံသွေဖည်မှု ဟုလည်း ခေါ်သည် ၊ သည် ကိန်းဂဏန်း ကွဲလွဲမှု၏ အတိုင်းအတာတစ်ခုဖြစ်သည်။ တစ်နည်းဆိုရသော် စံသွေဖည်မှုသည် ကိန်းဂဏန်းအချက်အလက်အစုတစ်ခု၏ ကွဲလွဲမှုကို ညွှန်ပြသည့် တန်ဖိုးတစ်ခုဖြစ်သည်။
ထို့ကြောင့်၊ စံသွေဖည်မှု (သို့မဟုတ် စံသွေဖည်မှု) ကို လူဦးရေ သို့မဟုတ် စာရင်းအင်းနမူနာ၏ ကွဲလွဲမှုကို တွက်ချက်ရန် အသုံးပြုသည်။ ဒေတာစီးရီးတစ်ခု၏ စံသွေဖည်မှု ကြီးမားလေ၊ ဒေတာ ကွဲကွာလေလေဖြစ်သည်။ စံသွေဖည်မှု နည်းနေပါက ယေဘုယျအားဖြင့် ဒေတာသည် ၎င်း၏ ဆိုလိုရင်းနှင့် အလွန်နီးစပ်သည်ဟု အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည်။
လူဦးရေအပေါ် စံနှုန်း သို့မဟုတ် ပုံမှန်သွေဖည်မှုကို တွက်ချက်သောအခါ၊ စံသွေဖည်မှုအတွက် သင်္ကေတ မှာ ဂရိအက္ခရာ sigma (σ) ဖြစ်သည်။ သို့သော် နမူနာစံသွေဖည်ခြင်းနှင့်ပတ်သက်လာလျှင် ကိန်းဂဏန်းတိုင်းတာခြင်းအတွက် အက္ခရာ s ကိုအသုံးပြုသည်။
အချို့သော စာရင်းဇယားများနှင့် ဖြစ်နိုင်ခြေရှိသော စာအုပ်များတွင် စံသွေဖည်မှုကို စံသွေဖည်မှုဟုလည်း ခေါ်သည်။
စံသွေဖည်မှု (သို့မဟုတ် စံသွေဖည်မှု) ဖော်မြူလာ
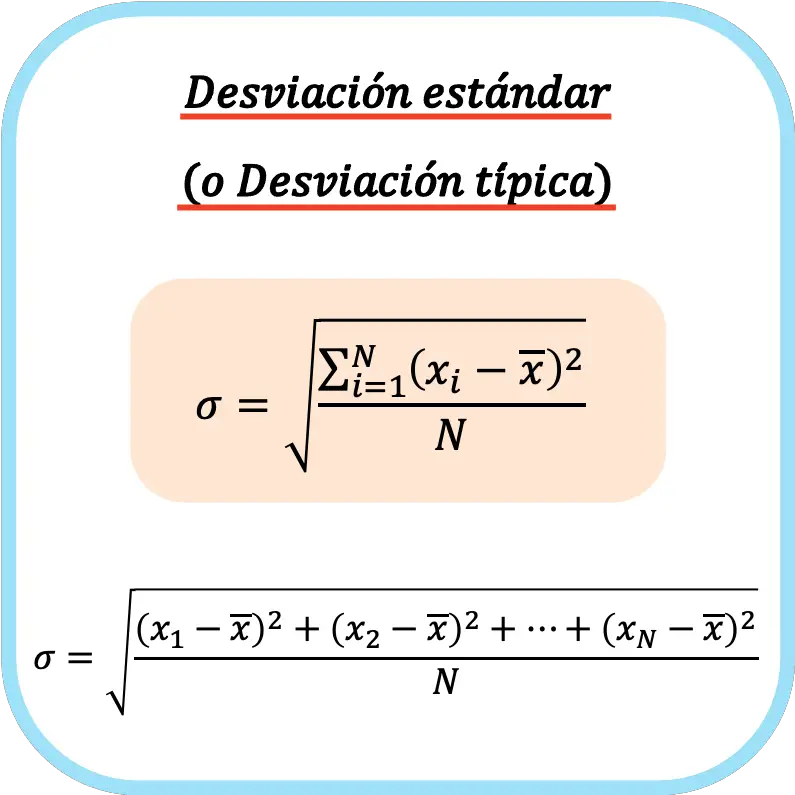
စံသွေဖည်မှု (သို့မဟုတ် စံသွေဖည်မှု) သည် ဒေတာစီးရီးများ၏ သွေဖည်မှုများ၏ နှစ်ထပ်ကိန်းများ၏ နှစ်ထပ်ကိန်းများနှင့် ညီမျှသည်။
ထို့ကြောင့် စံသွေဖည်မှု (သို့မဟုတ် စံသွေဖည်မှု) ကို တွက်ချက်ရန်အတွက် ဖော်မြူလာမှာ –
👉 မည်သည့်ဒေတာအစုံ၏ စံသွေဖည်မှုကို တွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ကို သင်အသုံးပြုနိုင်ပါသည်။
နိဂုံးချုပ်အနေဖြင့် ဒေတာအတွဲတစ်ခု၏ စံသွေဖည်မှုကို ရှာဖွေရန်၊ သင်သွေဖည်မှုအားလုံးကို တွက်ချက်ရန် လိုအပ်သည် (ဒေတာအမှတ်နှင့် ဂဏန်းသင်္ချာပျမ်းမျှအကြား ခြားနားချက်အဖြစ် သတ်မှတ်ထားသည်)၊ သွေဖည်မှုများကို နှစ်ခုသို့တိုး၍ ၎င်းတို့အားလုံးကို ပေါင်းထည့်ကာ ၎င်းဖြင့် ပိုင်းခြားပါ။ စုစုပေါင်း ဒေတာအရေအတွက်၊ နောက်ဆုံးတွင် square root ကိုယူပါ။
စံသွေဖည်မှု ဥပမာ (သို့မဟုတ် စံသွေဖည်မှု)
စံသွေဖည်မှု (သို့မဟုတ် ပုံမှန်သွေဖည်မှု) ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို ထည့်သွင်းစဉ်းစားခြင်းဖြင့် အောက်တွင် အဆင့်ဆင့်သော ဥပမာတစ်ခုဖြစ်ပြီး ဒေတာစီးရီးတစ်ခု၏ စံသွေဖည်မှုကို မည်ကဲ့သို့ တွက်ချက်သည်ကို သင်ကြည့်ရှုနိုင်ပါသည်။
- အောက်ပါတန်ဖိုးများ၏ စံသွေဖည်မှုကို တွက်ချက်ပါ- 3၊ 6၊ 2၊ 9၊ 4။
ပထမဆုံးလုပ်ရမှာက နမူနာဆိုလိုရင်းကို ဆုံးဖြတ်ပါ။ ဒါကိုလုပ်ဖို့၊ ဒေတာအားလုံးကို ပေါင်းပြီး စုစုပေါင်း လေ့လာတွေ့ရှိချက် အရေအတွက်အားဖြင့် ငါးခု ခွဲပါတယ်။
![]()
ယခု ကျွန်ုပ်တို့သည် စံသွေဖည်သော ဖော်မြူလာကို အသုံးပြုသည်-

ကျွန်ုပ်တို့သည် ဒေတာကို ဖော်မြူလာအဖြစ် အစားထိုးသည်-
![]()
နောက်ဆုံးတွင် ကျွန်ုပ်တို့သည် စံသွေဖည်မှုကို တွက်ချက်သည်-
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle\sigma & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{5}}\\[2ex]&= \sqrt{\frac{30,8}{5}}=\sqrt{6,16}=2,48 \end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d52b5396ff383310226cf152a9bf87ea_l3.png)
Standard Deviation (သို့မဟုတ် Standard Deviation) ဂဏန်းတွက်စက်
၎င်း၏စံသွေဖည်မှု (သို့မဟုတ် စံသွေဖည်) ကိုတွက်ချက်ရန် အောက်ပါအွန်လိုင်းဂဏန်းတွက်စက်ထဲသို့ ကိန်းဂဏန်းအချက်အလက်အစုအဝေးကို ထည့်ပါ။ ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။
အုပ်စုဖွဲ့ဒေတာအတွက် စံ (သို့မဟုတ် ပုံမှန်) သွေဖည်မှု
ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ထားသော ဒေတာများ၏ စံသွေဖည်မှု (သို့မဟုတ် စံသွေဖည်) ကို တွက်ချက်ရန် ၊ အောက်ပါအဆင့်များကို လိုက်နာရပါမည်-
- အုပ်စုဖွဲ့ဒေတာ၏ ဆိုလိုရင်းကို ရှာပါ။
- အုပ်စုဖွဲ့ဒေတာ၏သွေဖည်မှုများကိုတွက်ချက်ပါ။
- စတုရန်းတစ်ခုစီကွာဟချက်။
- ယခင်ရလဒ်တစ်ခုစီကို ၎င်း၏ကြားကာလ၏ကြိမ်နှုန်းဖြင့် မြှောက်ပါ။
- ယခင်အဆင့်တွင်ရရှိသောတန်ဖိုးများအားလုံး၏ပေါင်းလဒ်ကိုထည့်ပါ။
- စုစုပေါင်း လေ့လာတွေ့ရှိချက်အရေအတွက်ဖြင့် ပိုင်းခြားပါ။
- ယခင်တန်ဖိုး၏ နှစ်ထပ်ကိန်းကို ယူပါ။ ရလဒ်နံပါတ်သည် အုပ်စုဖွဲ့ဒေတာ၏ စံသွေဖည်မှုဖြစ်သည်။
နိဂုံးချုပ်အားဖြင့်၊ ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ထားသော ဒေတာစံသွေဖည်မှုကို တွက်ချက်ရန်အတွက် ဖော်မြူလာမှာ-
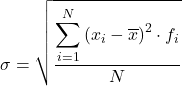
အထက်ဖော်ပြပါ ဖော်မြူလာကို ပုံမှန်အားဖြင့် အသုံးပြုသော်လည်း၊ တူညီသောရလဒ်ကို ရရှိသောကြောင့် အောက်ပါ အက္ခရာသင်္ချာအသုံးအနှုန်းကိုလည်း အသုံးပြုနိုင်သည်။
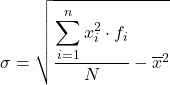
ထို့ကြောင့် ဤအရာအား မည်သို့လုပ်ဆောင်သည်ကို သင်မြင်နိုင်သည်၊ အောက်တွင် ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ထားသော အချက်အလက်များ၏ စံသွေဖည်မှုအပေါ် အဆင့်ဆင့် လေ့ကျင့်ခန်းတစ်ခုဖြစ်သည်။ ပိုမိုတိကျစွာ၊ အောက်ဖော်ပြပါ စာရင်းအင်းအချက်အလက်များ၏ စံသွေဖည်မှုကို တွက်ချက်ပါမည်-
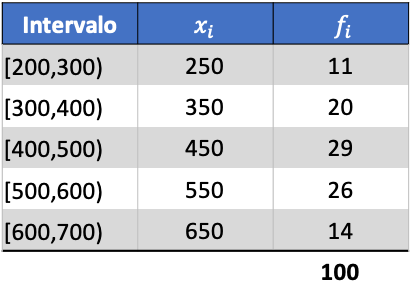
ပထမဦးစွာ၊ ကျွန်ုပ်တို့သည် ဂဏန်းသင်္ချာဆိုလိုအား တွက်ချက်ရန်အတွက် ကြားကာလတစ်ခုစီ၏ အတန်းရမှတ်ကို ၎င်း၏ကြိမ်နှုန်းဖြင့် မြှောက်သည်-
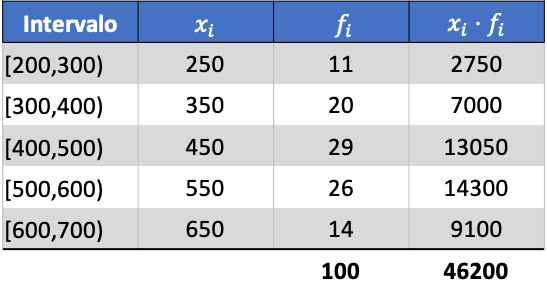
ထို့ကြောင့် အုပ်စုဖွဲ့ထားသောဒေတာများ၏ ပျမ်းမျှသည်-
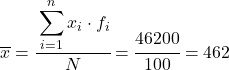
ယခု ကျွန်ုပ်တို့သည် ပျမ်းမျှတန်ဖိုးကို သိလာသောအခါ၊ ဒေတာဇယားတွင် အောက်ပါကော်လံသုံးခုကို ထည့်ရန်လိုအပ်သည်-
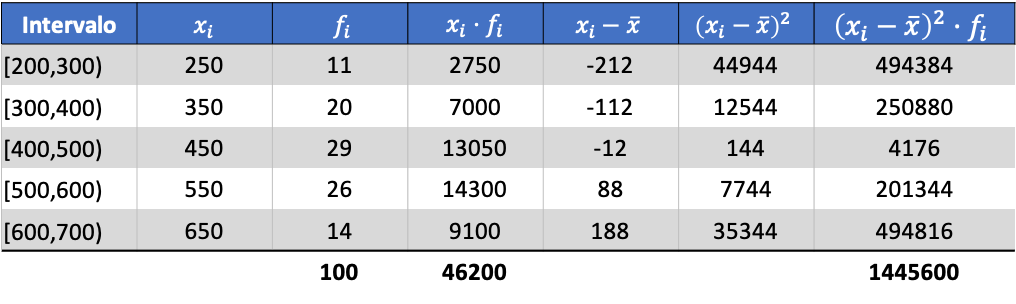
ထို့နောက် အုပ်စုဖွဲ့ဒေတာ၏ စံသွေဖည်မှုသည် နောက်ဆုံးကော်လံ၏ စုစုပေါင်း၏ နှစ်ထပ်ကိန်း၏ ရလဒ်ဖြစ်လိမ့်မည်-
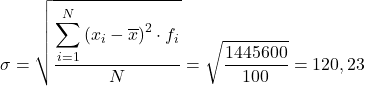
စံ (သို့မဟုတ် ပုံမှန်) သွေဖည်မှုနှင့် ကွဲလွဲမှု
စံသွေဖည်မှု (သို့မဟုတ် ပုံမှန်သွေဖည်မှု) နှင့် ကွဲလွဲမှုအကြား ဆက်နွယ်မှု မှာ စံသွေဖည်မှုမှာ ကွဲလွဲမှု၏ နှစ်ထပ်ကိန်းရင်းဖြစ်သည်။
ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် ဒေတာအတွဲတစ်ခု၏ ကွဲလွဲမှုတန်ဖိုးကို သိပါက၊ စံသွေဖည်မှုကို စတုရန်းအမြစ်ကိုယူပြီး အလွယ်တကူ တွက်ချက်နိုင်သည်။ သို့မဟုတ် အပြန်အလှန်အားဖြင့်၊ ကျွန်ုပ်တို့သည် စံသွေဖည်မှုကို သိပါက၊ တန်ဖိုးကို နှစ်ခြမ်းခွဲခြင်းဖြင့် ကွဲလွဲမှုကို ရှာဖွေနိုင်သည်။
![]()
အမှန်မှာ၊ နှစ်ထပ်စံသွေဖည်ခြင်းသင်္ကေတကို အသုံးပြု၍ ကွဲပြားမှုကို ရိုးရိုးရှင်းရှင်း ကိုယ်စားပြုနိုင်သည်။ ထို့ကြောင့် လူဦးရေကွဲလွဲမှုအတွက် သင်္ကေတသည် sigma နှစ်ထပ်ကိန်း (σ 2 ) ဖြစ်ပြီး နမူနာကွဲလွဲမှုအတွက် သင်္ကေတသည် s နှစ်ထပ်ကိန်း (s 2 ) ဖြစ်သည်။
ထို့အပြင်၊ စံသွေဖည်မှုနှင့် ကွဲလွဲမှုဆိုင်ရာ အယူအဆနှစ်ခုလုံးသည် ကိန်းဂဏန်း အချက်အလက်များစွာ၏ ကွဲလွဲမှုကို ပြသသောကြောင့် တူညီသော အဓိပ္ပာယ်ဖွင့်ဆိုချက်တစ်ခုရှိသည်။
စံသွေဖည်ခြင်း၏ ဂုဏ်သတ္တိများ (သို့မဟုတ် စံသွေဖည်မှု)
စံသွေဖည်မှုတွင် အောက်ပါဂုဏ်သတ္တိများရှိသည်။
- ဒေတာနမူနာတစ်ခု၏ စံသွေဖည်မှုသည် အနုတ်လက္ခဏာမဖြစ်နိုင်ပါ။
![]()
- ဒေတာအားလုံးတူညီပါက စံသွေဖည်မှု သုညဖြစ်ပါမည်။
![]()
- ကိန်းသေတစ်ခုအား ဒေတာအားလုံးသို့ ပေါင်းထည့်ပါက၊ စံသွေဖည်မှုတန်ဖိုးသည် ပြောင်းလဲမည်မဟုတ်ပါ။
![]()
- ဒေတာအားလုံးကို ဂဏန်းတစ်ခုဖြင့် မြှောက်ပါက၊ စံသွေဖည်မှုကို ထိုနံပါတ်၏ ပကတိတန်ဖိုးဖြင့် မြှောက်မည်ဖြစ်သည်။
![]()
- ကျပန်း variable နှစ်ခု၏ စံသွေဖည်မှု ပေါင်းလဒ်သည် variable များ၏ ကွဲပြားမှုများ၏ ပေါင်းလဒ်၏ နှစ်ထပ်ကိန်းနှင့် ညီမျှပြီး ကိန်းရှင်နှစ်ခုကြားရှိ ကွဲလွဲမှု နှစ်ဆဖြစ်သည်။
![]()
- မတူညီသောဖြန့်ဝေမှုများ (σ i ) နှင့် ၎င်းတို့၏ ဒေတာအရေအတွက် (n i ) တို့၏ စံသွေဖည်မှုများကို သိရှိပါက အောက်ပါဖော်မြူလာကို အသုံးပြုခြင်းဖြင့် စုစုပေါင်းစံသွေဖည်မှုကို တွက်ချက်နိုင်သည်-