နမူနာဖြန့်ချီခြင်းကို ဆိုလိုသည်။

အားဖြင့် Benjamin Anderson ဩဂုတ် 3, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် ကိန်းဂဏန်းနမူနာဖြန့်ဝေခြင်းဆိုသည်မှာ အဘယ်အရာကိုဆိုလိုကြောင်း ရှင်းပြထားသည်။ ပျမ်းမျှနမူနာဖြန့်ဝေမှုဖော်မြူလာနှင့် အဆင့်ဆင့်ဖြေရှင်းထားသော လေ့ကျင့်ခန်းကိုလည်း သင်တွေ့လိမ့်မည်။

ဆိုလိုချက်၏နမူနာဖြန့်ဝေမှုသည် အဘယ်နည်း။

ပျမ်းမျှနမူနာဖြန့်ဝေခြင်း (သို့မဟုတ် နမူနာဖြန့်ဝေမှုနည်းလမ်းများ ) သည် လူဦးရေတစ်ခုစီမှဖြစ်နိုင်သောနမူနာတစ်ခုစီ၏နမူနာပျမ်းမျှကို တွက်ချက်ခြင်းမှ ထွက်ပေါ်လာသော ဖြန့်ဖြူးမှုဖြစ်သည်။ ဆိုလိုသည်မှာ၊ နမူနာ အစု၏ အဓိပ္ပါယ်မှာ လူဦးရေတစ်ခုမှ ဖြစ်နိုင်ခြေရှိသော နမူနာများအားလုံးကို ဆိုလိုခြင်း၏နမူနာခွဲဝေမှုကို ပုံဖော်သည်။

သို့မဟုတ် တစ်နည်းဆိုရသော် ကျွန်ုပ်တို့သည် လူဦးရေတစ်ခုမှယူနိုင်သောနမူနာအားလုံးကို လေ့လာပြီး နမူနာတစ်ခုစီ၏ပျမ်းမျှအား တွက်ချက်ပါက၊ တွက်ချက်ထားသောတန်ဖိုးများအစုသည် နမူနာ၏နမူနာခွဲဝေမှုကို ဆိုလိုသည်။

စာရင်းဇယားများတွင်၊ နမူနာတစ်ခုအား ခွဲခြမ်းစိတ်ဖြာသောအခါတွင် လူဦးရေ၏ ဆိုလိုရင်းတန်ဖိုးသို့ ချဉ်းကပ်နိုင်ခြေကို တွက်ချက်ရန် အသုံးပြုသည်။

ဆိုလိုရင်း၏နမူနာဖြန့်ဝေခြင်းအတွက် ဖော်မြူလာ

သာမန်ဖြစ်နိုင်ခြေဖြန့်ဝေမှုအား ပျမ်းမျှအားဖြင့် လိုက်နာသော လူဦးရေကို ပေးသည်။

$\mu$

နှင့် စံသွေဖည်ခြင်း။

$\sigma$

နှင့် အရွယ်အစားနမူနာများကို ထုတ်ယူသည်။

$n$

၊ ပျမ်းမျှ၏နမူနာဖြန့်ဝေမှုကိုလည်း အောက်ပါလက္ခဏာများပါရှိသော ပုံမှန်ဖြန့်ဖြူးမှုဖြင့် သတ်မှတ်ပေးလိမ့်မည်-

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

ရွှေ

$\mu_{\overline{x}}$

ဆိုသည်မှာ ပျမ်းမျှ နှင့် ဥပမာ ဖြန့်ဝေခြင်း၏ ဆိုလိုရင်းဖြစ်သည်။

$\sigma_{\overline{x}}$

၎င်း၏စံသွေဖည်မှုဖြစ်သည်။ ထိုမျှသာမက၊

$\cfrac{\sigma}{\sqrt{n}}$

နမူနာဖြန့်ဝေမှု၏ စံအမှားဖြစ်သည်။

မှတ်ချက်- လူဦးရေသည် ပုံမှန်ဖြန့်ဝေမှုကို မလိုက်နာသော်လည်း နမူနာအရွယ်အစားသည် ကြီးမားပါက (n>30)၊ ဆိုလိုရင်း၏နမူနာဖြန့်ဝေမှုကို ဗဟိုကန့်သတ်သီအိုရီဖြင့် ယခင်ပုံမှန်ဖြန့်ဝေမှုတွင်လည်း ခန့်မှန်းနိုင်သည်။

ထို့ကြောင့်၊ ဆိုလိုရင်း၏နမူနာဖြန့်ဝေမှုသည် သာမန်ဖြန့်ဖြူးမှုတစ်ခုနောက်တွင်ရှိသောကြောင့်၊ နမူနာဆိုလိုမှုနှင့်ပတ်သက်၍ ဖြစ်နိုင်ခြေတစ်စုံတစ်ရာကို တွက်ချက်ရန်အတွက် ဖော်မြူလာ မှာ-

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

ရွှေ-

$\overline{x}$

နမူနာဆိုလိုသည်။
$\mu$

ဒါက လူဦးရေ ပျမ်းမျှပါ။
$s$

လူဦးရေစံနှုန်းသွေဖည်သည်။
$n$

နမူနာအရွယ်အစားဖြစ်သည်။
$Z$

စံပုံမှန်ဖြန့်ဝေမှု N(0,1) မှသတ်မှတ်ထားသော ကိန်းရှင်တစ်ခုဖြစ်သည်။

ဆိုလိုတာက နမူနာဖြန့်ချီခြင်းရဲ့ လက်တွေ့ကမ္ဘာဥပမာ

အဓိပ္ပါယ်၏နမူနာခွဲဝေမှု၏ အဓိပ္ပါယ်နှင့် ၎င်း၏ဆက်စပ်ဖော်မြူလာများသည် အဘယ်အရာဖြစ်သည်ကို မြင်ပြီးနောက်၊ သဘောတရားကို ပိုနားလည်ရန် ဥပမာတစ်ခုကို ဖြေရှင်းကြည့်ကြပါစို့။

တက္ကသိုလ်ကျောင်းသားများ၏အလေးချိန်သည် ပျမ်းမျှအားဖြင့် 68 ကီလိုဂရမ်နှင့် စံသွေဖည်မှု 9 ကီလိုဂရမ်ဖြင့် ပုံမှန်ဖြန့်ဝေမှုနောက်တွင် လိုက်နေသည်။ သတ်မှတ်သည်-
1. ကျောင်းသား 25 ယောက်၏ ကျပန်းနမူနာတစ်ခု၏ ပျမ်းမျှသည် 66 ကီလိုဂရမ်အောက် ဖြစ်နိုင်ချေရှိသနည်း။
2. နမူနာ 300 ကို ကျောင်းသား 25 ယောက်စီ အရွယ်အစားဖြင့် ယူပါက၊ နမူနာ ပျမ်းမျှ မည်မျှ တန်ဖိုး 66 ကီလိုဂရမ်အောက် ရှိမည်နည်း။

ပထမဦးစွာ၊ ကျွန်ုပ်တို့သည် သက်ဆိုင်ရာ ကိန်းဂဏန်းတန်ဖိုးကို တွက်ချက်ရမည်ဖြစ်ပြီး၊ ဤအတွက်၊ ကျွန်ုပ်တို့သည် အထက်တွင်မြင်ခဲ့သော ဖော်မြူလာကို ကျင့်သုံးသည်-

$\displaystyle Z=\frac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}=\frac{66-68}{\displaystyle\frac{9}{\sqrt{25}}}=-1,11$

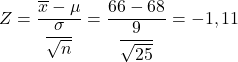
ထို့ကြောင့် ကျွန်ုပ်တို့ရှာဖွေနေသော ဖြစ်နိုင်ခြေသည် Z = ဖြစ်နိုင်ခြေဇယားမှ အလွယ်တကူ ရယူနိုင်သည့် စံပုံမှန်ဖြန့်ဝေမှု၏ ဘယ်ဘက်အမြီး၏ Z=-1.11 တန်ဖိုးနှင့် သက်ဆိုင်ပါသည်။ ထို့ကြောင့် ပြဿနာက ကျွန်ုပ်တို့ကို မေးသည့် ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ရန် Z ဇယားကို အသုံးပြုသည်-

$P[\overline{x}\leq 66]=P[Z\leq -1,11] =0,1335$

➤ ဇယား Z ကိုကြည့်ပါ။

ယခု ကျွန်ုပ်တို့သည် ကျပန်းနမူနာ၏ဆိုလိုရင်း 66 ကီလိုဂရမ်ထက်နည်းသောဖြစ်နိုင်ခြေကိုသိရန်၊ နမူနာအရေအတွက် 66 ကီလိုဂရမ်အောက်ဆိုလိုသည်မှာ တူညီသောနမူနာ 300 ကိုယူပြီး 66 ကီလိုဂရမ်အောက်ဆိုလိုသည်၊ ကျွန်ုပ်တို့ယူထားသောနမူနာစုစုပေါင်းအရေအတွက်ဖြင့် တွက်ချက်ထားသောဖြစ်နိုင်ခြေကို မြှောက်ရန် လိုအပ်သည်-

$0,1335\cdot 300 =40,05 \approx 40$

ထို့ကြောင့် ထုတ်ယူထားသောနမူနာ ၄၀ ခန့်သည် ပျမ်းမျှအားဖြင့် ၆၆ ကီလိုဂရမ်အောက် ရှိမည်ဖြစ်သည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။

ဆိုလိုချက်၏နမူနာဖြန့်ဝေမှုသည် အဘယ်နည်း။

ဆိုလိုရင်း၏နမူနာဖြန့်ဝေခြင်းအတွက် ဖော်မြူလာ

ဆိုလိုတာက နမူနာဖြန့်ချီခြင်းရဲ့ လက်တွေ့ကမ္ဘာဥပမာ

စာရေးသူအကြောင်း

Benjamin Anderson

မှတ်ချက်တစ်ခုထည့်ပါ။