ဆိုလိုရင်းအတွက် ယူဆချက် စမ်းသပ်ခြင်း။

အားဖြင့် Benjamin Anderson ဩဂုတ် 3, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးသည် ကိန်းဂဏန်းစာရင်းဇယားများတွင် ဆိုလိုချက်အတွက် မည်ကဲ့သို့ယူဆချက်စမ်းသပ်ခြင်းအကြောင်း ရှင်းပြထားသည်။ ထို့ကြောင့်၊ သင်သည် ပျမ်းမျှအတွက် သီအိုရီစမ်းသပ်ဖော်မြူလာကို တွေ့ရမည်ဖြစ်ပြီး၊ ထို့အပြင် လေ့ကျင့်ခန်းတစ်ခုပြီးတစ်ခု အဆင့်ဆင့်ဖြေရှင်းထားသည်။

ဆိုလိုရင်းအတွက် hypothesis testing ဆိုတာ ဘာလဲ။

ပျမ်းမျှအတွက် တွေးခေါ်မှုစမ်းသပ်ခြင်း သည် လူဦးရေဆိုလိုချက်၏ null hypothesis ကို ငြင်းပယ်ရန် သို့မဟုတ် ငြင်းပယ်ရန် အသုံးပြုသည့် ကိန်းဂဏန်းဆိုင်ရာ နည်းလမ်းတစ်ခုဖြစ်သည်။

ပို၍တိကျသည်မှာ၊ ဆိုလိုရင်းအတွက် သီအိုရီစမ်းသပ်ခြင်းတွင် စစ်ဆေးမှုစာရင်းအင်းကို တွက်ချက်ခြင်းနှင့် null hypothesis ကို ငြင်းပယ်ခြင်း သို့မဟုတ် မငြင်းရန် အရေးကြီးသောတန်ဖိုးနှင့် နှိုင်းယှဉ်ခြင်းတို့ ပါဝင်ပါသည်။

သီအိုရီစစ်ဆေးမှုများတွင် အမည်အမျိုးမျိုးရှိသည်ကို သတိပြုသင့်သည်။ ကိန်းဂဏန်းစာရင်းဇယားများတွင် ၎င်းတို့ကို အယူအဆကွဲလွဲမှုများ၊ သီအိုရီစမ်းသပ်မှုများ၊ သို့မဟုတ် အရေးပါမှုစမ်းသပ်မှုများဟုလည်း ခေါ်သည်။

ဆိုလိုရင်းအတွက် အယူအဆစမ်းသပ်ခြင်းဖော်မြူလာ

ထို့နောက် ပျမ်းမျှတွက်ဆချက်အတွက် သီအိုရီစမ်းသပ်မှု ကိန်းဂဏန်းကို မည်ကဲ့သို့ တွက်ချက်သည်ကို ကျွန်ုပ်တို့ကြည့်ပါမည်။ သို့သော်လည်း ဖော်မြူလာသည် ကွဲလွဲမှုကို သိသည် သို့မဟုတ် မသိပေါ် မူတည်၍ အနည်းငယ် ကွဲပြားသည်၊ ထို့ကြောင့် ကွဲလွဲမှုကို သိသောအခါ ကွဲလွဲမှုကို သိသောအခါ၊ ကွဲလွဲမှုကို မသိသောအခါတွင် မည်သို့လုပ်ဆောင်သည်ကို ဦးစွာကြည့်ရှုပါမည်။

သွေဖည်ခြင်း ဖြင့် သိသည်။

ပျမ်းမျှကွဲလွဲမှုကို သိရှိထားသည့်အတွက် စမ်းသပ်ခြင်းဆိုင်ရာ အယူအဆဖော်မြူလာ မှာ-

$\displaystyle Z=\frac{\overline{x}-\mu}{\displaystyle \frac{\sigma}{\sqrt{n}}}$

ရွှေ-

$Z$

ဆိုသည်မှာ ပျမ်းမျှအတွက် hypothesis test statistic ဖြစ်သည်။
$\overline{x}$

နမူနာဆိုလိုသည်။
$\mu$

အဆိုပြုထားသော ပျမ်းမျှတန်ဖိုးဖြစ်သည်။
$\sigma$

လူဦးရေစံနှုန်းသွေဖည်သည်။
$n$

နမူနာအရွယ်အစားဖြစ်သည်။

ပျမ်းမျှတွက်ဆချက်အတွက် စမ်းသပ်မှုကိန်းဂဏန်းကို တွက်ချက်ပြီးသည်နှင့် null hypothesis ကို ငြင်းပယ်ရန် သို့မဟုတ် ငြင်းပယ်ရန် ရလဒ်ကို အဓိပ္ပာယ်ပြန်ဆိုသင့်သည်-

ပျမ်းမျှအတွက် သီအိုရီစစ်ဆေးမှုသည် နှစ်ဖက်သဘောတူပါက၊ စာရင်းအင်း၏ ပကတိတန်ဖိုးသည် အရေးကြီးသောတန်ဖိုး Z _α/2 ထက် ကြီးနေပါက null hypothesis ကို ပယ်ချပါသည်။
ပျမ်းမျှတွက်ဆချက်စစ်ဆေးမှုသည် မှန်ကန်သောအမြီးနှင့်ကိုက်ညီပါက၊ ကိန်းဂဏန်းသည် အရေးကြီးသောတန်ဖိုး Z _α ထက်ကြီးပါက null hypothesis ကို ပယ်ချပါသည်။
ပျမ်းမျှတွက်ဆချက်စစ်ဆေးမှုသည် ဘယ်အမြီးနှင့်ကိုက်ညီပါက၊ ကိန်းဂဏန်းသည် အရေးကြီးသောတန်ဖိုး -Z _α ထက်နည်းပါက null hypothesis ကို ပယ်ချပါသည်။

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}$

ဤကိစ္စတွင်၊ အရေးကြီးသောတန်ဖိုးများကို စံသတ်မှတ်ထားသော ပုံမှန်ဖြန့်ချီရေးဇယား မှ ရရှိသည်။

မသိသောကွဲလွဲမှုဖြင့်

အမည်မသိကွဲလွဲမှုရှိသော ပျမ်းမျှအတွက် စမ်းသပ်မှုယူဆချက်ဖော်မြူလာ မှာ-

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

ရွှေ-

$t$

ကျောင်းသား၏ t ဖြန့်ဝေမှု ဖြင့် သတ်မှတ်ထားသော ပျမ်းမျှအတွက် သီအိုရီစစ်ဆေးမှု ကိန်းဂဏန်းဖြစ်သည်။
$\overline{x}$

နမူနာဆိုလိုသည်။
$\mu$

အဆိုပြုထားသော ပျမ်းမျှတန်ဖိုးဖြစ်သည်။
$s$

နမူနာစံသွေဖည်သည်။
$n$

နမူနာအရွယ်အစားဖြစ်သည်။

ယခင်ကဲ့သို့ပင်၊ စမ်းသပ်စာရင်းအင်း၏ တွက်ချက်ထားသောရလဒ်သည် null အယူအဆကို ငြင်းပယ်ရန် သို့မဟုတ် ငြင်းပယ်ရန် အရေးကြီးသောတန်ဖိုးဖြင့် အဓိပ္ပာယ်ပြန်ဆိုရပါမည်-

ပျမ်းမျှအတွက် သီအိုရီစစ်ဆေးမှုသည် နှစ်ဖက်သဘောတူပါက၊ စာရင်းအင်း၏ ပကတိတန်ဖိုးသည် အရေးကြီးသောတန်ဖိုး t _α/2|n-1 ထက်ကြီးပါက null hypothesis ကို ပယ်ချပါသည်။
ပျမ်းမျှတွက်ဆချက်စစ်ဆေးမှုသည် မှန်ကန်သောအမြီးနှင့်ကိုက်ညီပါက၊ ကိန်းဂဏန်းသည် အရေးကြီးသောတန်ဖိုး t _α|n-1 ထက်ကြီးပါက null hypothesis ကို ပယ်ချပါသည်။
ပျမ်းမျှတွက်ဆချက်စစ်ဆေးမှုသည် ဘယ်အမြီးနှင့်ကိုက်ညီပါက၊ ကိန်းဂဏန်းသည် အရေးကြီးသောတန်ဖိုး -t _α|n-1 ထက်နည်းပါက null hypothesis ကို ပယ်ချပါသည်။

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

ကွဲလွဲမှုကို မသိသောအခါ၊ အရေးကြီးသော စမ်းသပ်မှုတန်ဖိုးများကို ကျောင်းသား၏ ဖြန့်ဖြူးမှုဇယားမှ ရယူသည်။

ဆိုလိုရင်းအတွက် အစစ်အမှန်ကမ္ဘာနမူနာ၊

လူဦးရေအတွက်ဆိုလိုသည့် သီအိုရီစမ်းသပ်ခြင်း၏ သဘောတရားကို အပြည့်အဝနားလည်ရန်၊ ဤယူဆချက်စမ်းသပ်ခြင်းအမျိုးအစား၏ လက်တွေ့ဘဝဥပမာကို အောက်တွင် ကြည့်ရှုနိုင်ပါသည်။

၎င်းလက်ပ်တော့၏ဘက်ထရီသည် 6 နာရီကြာခံသည်ဟုနည်းပညာကုမ္ပဏီတစ်ခုကပြောကြားခဲ့သည်။ သိသာထင်ရှားမှုအဆင့် α = 0.05 ဖြင့် သီအိုရီစစ်ဆေးမှုကို လုပ်ဆောင်ခြင်းဖြင့် ဤယူဆချက်သည် မှားယွင်းခြင်းရှိမရှိ စစ်ဆေးပါသည်။ ဒီလိုလုပ်ဖို့၊ အလုံးရေ 20 ကိုဝယ်ပြီး ကွန်ပျူတာတစ်လုံးစီရဲ့ ဘက်ထရီသက်တမ်းကို စောင့်ကြည့်ဖို့ ဆုံးဖြတ်လိုက်တယ် (တန်ဖိုးတွေကို နာရီနဲ့ ဖော်ပြပါတယ်)။

၅.၂ ၅.၉ ၇.၁ ၄.၂ ၆.၅
၈.၅ ၄.၆ ၆.၈ ၆.၉ ၅.၈
၅.၁ ၆.၅ ၇.၀ ၅.၃ ၆.၂
၅.၇ ၆.၆ ၇.၅ ၅.၁ ၆.၁

ဤကိစ္စတွင်၊ ပျမ်းမျှနှင့်ပတ်သက်သော သီအိုရီစမ်းသပ်မှု၏ null နှင့် အခြားအခြားသော အယူအဆများသည် အောက်ပါအတိုင်းဖြစ်သည်-

$\begin{cases}H_0: \mu=6\\[2ex] H_1:\mu\neq 6 \end{cases}$

စမ်းသပ်စာရင်းအင်းကို ဆုံးဖြတ်ရန်အတွက်၊ ကျွန်ုပ်တို့သည် နမူနာစံနှုန်းနှင့် နမူနာစံသွေဖည်မှုကို ဦးစွာတွက်ချက်ရန် လိုအပ်သည်-

$\overline{x}=6,13 \qquad s=1,05$

လူဦးရေကွဲလွဲမှုကို ကျွန်ုပ်တို့မသိသောကြောင့် စစ်ဆေးမှုစာရင်းအင်းကိုရရှိရန် ကျွန်ုပ်တို့သည် အမည်မသိကွဲလွဲမှုရှိသော ပျမ်းမျှအတွက် တွေးခေါ်မှုစမ်းသပ်ဖော်မြူလာကို အသုံးပြုရန်လိုအပ်သည်-

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

$\displaystyle t=\frac{6,13-6}{\displaystyle \frac{1,05}{\sqrt{20}}}$

$\displaystyle t=0,68$

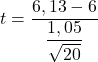
ယခု ကျွန်ုပ်တို့သည် သီအိုရီစမ်းသပ်မှု၏ အရေးပါသောတန်ဖိုးကို ရှာဖွေရန် လိုအပ်သည်၊ ထို့ကြောင့် သက်ဆိုင်သောတန်ဖိုးအတွက် ကျောင်းသား၏ t ဖြန့်ချီရေးဇယား တွင် ကြည့်ရှုပါ။ Student’s t ၏ လွတ်လပ်မှုဒီဂရီများသည် နမူနာအရွယ်အစား (20-1=19) ထက်နည်းပြီး အခြားတစ်ဖက်တွင်၊ သက်ဆိုင်ရာဖြစ်နိုင်ခြေသည် နှစ်ဘက်လုံးဖြစ်သောကြောင့် အရေးပါမှုအဆင့်ထက်ဝက် (0.05/2= 0.025) ဖြစ်သည်။ hypothesis စမ်းသပ်ခြင်း။

$\alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 19}=2,093\end{array}$

နိဂုံးချုပ်အနေဖြင့်၊ ဤသည်မှာ နှစ်ဖက်မြင်ယူဆချက်စမ်းသပ်မှုဖြစ်ပြီး စမ်းသပ်မှုစာရင်းအင်း၏ ပကတိတန်ဖိုးသည် အရေးကြီးသောတန်ဖိုးထက်နည်းသောကြောင့်၊ null hypothesis ကို ပယ်ချမည်မဟုတ်သော်လည်း အခြားယူဆချက်အား ပယ်ချပါသည်။

$0,68<2,093 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_1$

အဓိပ္ပါယ်မှာ ခြားနားချက်အတွက် ယူဆချက် စမ်းသပ်ခြင်း။

ခြားနားချက် ဆိုသည်မှာ လူနှစ်ဦး၏ အဓိပ္ပါယ်မှာ တူညီသည်ဟူသော null hypothesis ကို ငြင်းပယ်ရန် သို့မဟုတ် လက်ခံရန် အယူအဆ ဆိုင်ရာ စမ်းသပ်မှုကို အသုံးပြုသည်။

ထို့ကြောင့် အဓိပ္ပါယ်နှစ်မျိုး၏ ခြားနားချက်အတွက် သီအိုရီစမ်းသပ်မှုတစ်ခု၏ null hypothesis သည် အမြဲတမ်း အောက်ပါအတိုင်းဖြစ်သည် ။

$H_0: \mu_1=\mu_2$

အစားထိုးယူဆချက်သည် အောက်ပါသုံးမျိုးထဲမှ တစ်ခု ဖြစ်နိုင်သော်လည်း၊

$\begin{array}{l}H_1:\mu_1\neq \mu_2\\[2ex]H_1:\mu_1>\mu_2\\[2ex]H_1:\mu_1<\mu_2\end{array}$

ထို့နောက် ကွဲလွဲမှုကို သိရှိသည့်အခါ ခြားနားချက်အတွက် အယူအဆဆိုင်ရာ စမ်းသပ်ကိန်းဂဏန်းကို တွက်ချက်ရန် ဖော်မြူလာမှာ –

$\displaystyle Z=\frac{\displaystyle \overline{x_1}-\overline{x_2}}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

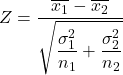
ရွှေ-

$Z$

စံပုံမှန်ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်သော သိထားသောကွဲလွဲမှုဖြင့် ဆိုလိုချက်နှစ်ခု၏ ခြားနားချက်အတွက် သီအိုရီစမ်းသပ်မှု ကိန်းဂဏန်းဖြစ်ပါသည်။
$\overline{x_1}$

နမူနာ 1 ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
$\overline{x_2}$

နမူနာ 2 ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
$\sigma_1^2$

လူဦးရေ ကွဲပြားမှု ၁။
$\sigma_2^2$

လူဦးရေ ကွဲပြားမှု ၂။
$n_1$

နမူနာအရွယ်အစား 1 ဖြစ်ပါတယ်။
$n_2$

နမူနာအရွယ်အစား 2 ဖြစ်ပါတယ်။

အခြားတစ်ဖက်တွင်၊ ကွဲလွဲမှုကို မသိရှိသည့်အခါ ခြားနားချက်အတွက် ပေါင်းစပ်ယူဆချက် စမ်းသပ်ကိန်းဂဏန်းကို တွက်ချက်ခြင်းအတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်။

$\displaystyle t=\frac{\displaystyle \overline{x_1}-\overline{x_2}}{\displaystyle\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

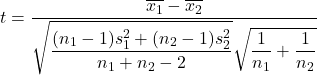
ရွှေ-

$t$

ကျောင်းသား၏ t ဖြန့်ဝေမှုကို လိုက်နာသော အမည်မသိကွဲလွဲမှုဖြင့် ဆိုလိုသည့် နှစ်ခု၏ ခြားနားချက်အတွက် သီအိုရီစမ်းသပ်မှု ကိန်းဂဏာန်းဖြစ်သည်။
$\overline{x_1}$

နမူနာ 1 ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
$\overline{x_2}$

နမူနာ 2 ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
$s_1^2$

နမူနာ 1 ၏ကွဲလွဲမှုဖြစ်သည်။
$s_2^2$

နမူနာ 2 ၏ကွဲလွဲမှုဖြစ်သည်။
$n_1$

နမူနာအရွယ်အစား 1 ဖြစ်ပါတယ်။
$n_2$

နမူနာအရွယ်အစား 2 ဖြစ်ပါတယ်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။

ဆိုလိုရင်းအတွက် hypothesis testing ဆိုတာ ဘာလဲ။

ဆိုလိုရင်းအတွက် အယူအဆစမ်းသပ်ခြင်းဖော်မြူလာ

သွေဖည်ခြင်း ဖြင့် သိသည်။

မသိသောကွဲလွဲမှုဖြင့်

ဆိုလိုရင်းအတွက် အစစ်အမှန်ကမ္ဘာနမူနာ၊

အဓိပ္ပါယ်မှာ ခြားနားချက်အတွက် ယူဆချက် စမ်းသပ်ခြင်း။

စာရေးသူအကြောင်း

Benjamin Anderson

မှတ်ချက်တစ်ခုထည့်ပါ။