ဇယားတစ်ခုမှ linear regression equation ကို ဘယ်လိုရှာမလဲ။

မကြာခဏ ဒေတာဇယားတစ်ခုမှ linear regression equation ကို သင်ရှာလိုပေမည်။

ဥပမာအားဖြင့်၊ သင်သည် အောက်ပါဒေတာဇယားကို လက်ခံရရှိသည်ဆိုပါစို့။

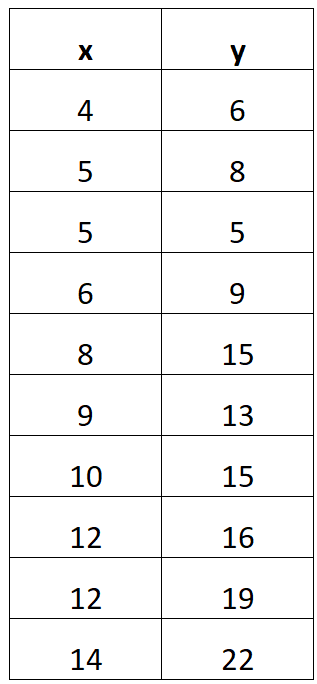
အောက်ဖော်ပြပါ အဆင့်ဆင့် ဥပမာသည် ဤဒေတာဇယားမှ မျဉ်းကြောင်းပြန်ဆုတ်ခြင်းညီမျှခြင်းကို မည်သို့ရှာဖွေရမည်ကို ပြသထားသည်။

အဆင့် 1- X*Y၊ X ² နှင့် Y ² ကို တွက်ချက်ပါ။

ဦးစွာ၊ အတန်းတစ်ခုစီအတွက် အောက်ပါမက်ထရစ်များကို တွက်ချက်ပါမည်။

• x*y
• ^x၂
• နှင့် ^၂

အောက်ပါစခရင်ရှော့တွင် ၎င်းကိုပြုလုပ်နည်းကို ပြသသည်-

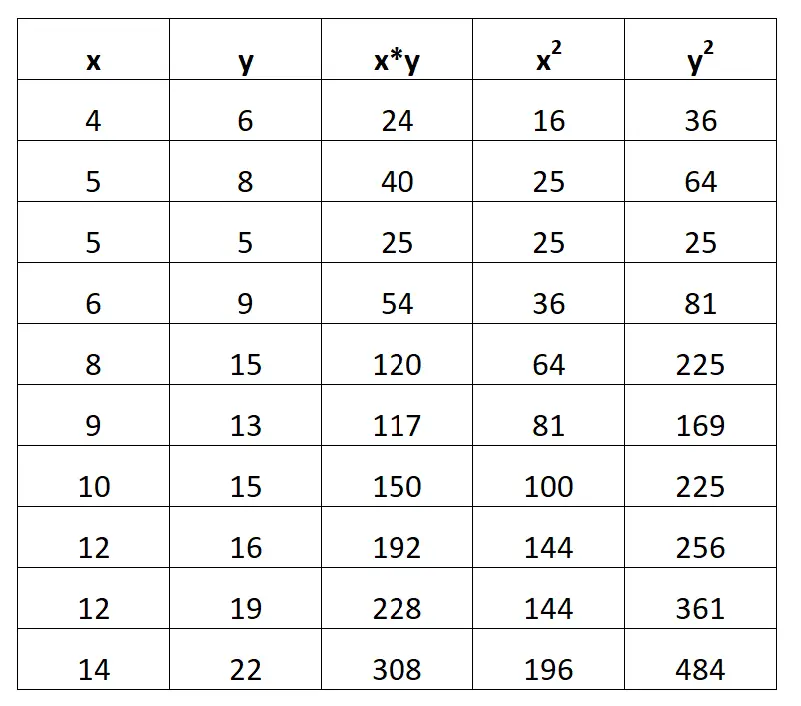
အဆင့် 2- ΣX၊ ΣY၊ ΣX*Y၊ ΣX ² နှင့် ΣY ² ကို တွက်ချက်ပါ

ထို့နောက်၊ ကော်လံတစ်ခုစီ၏ ပေါင်းလဒ်ကို တွက်ချက်ပါမည်-

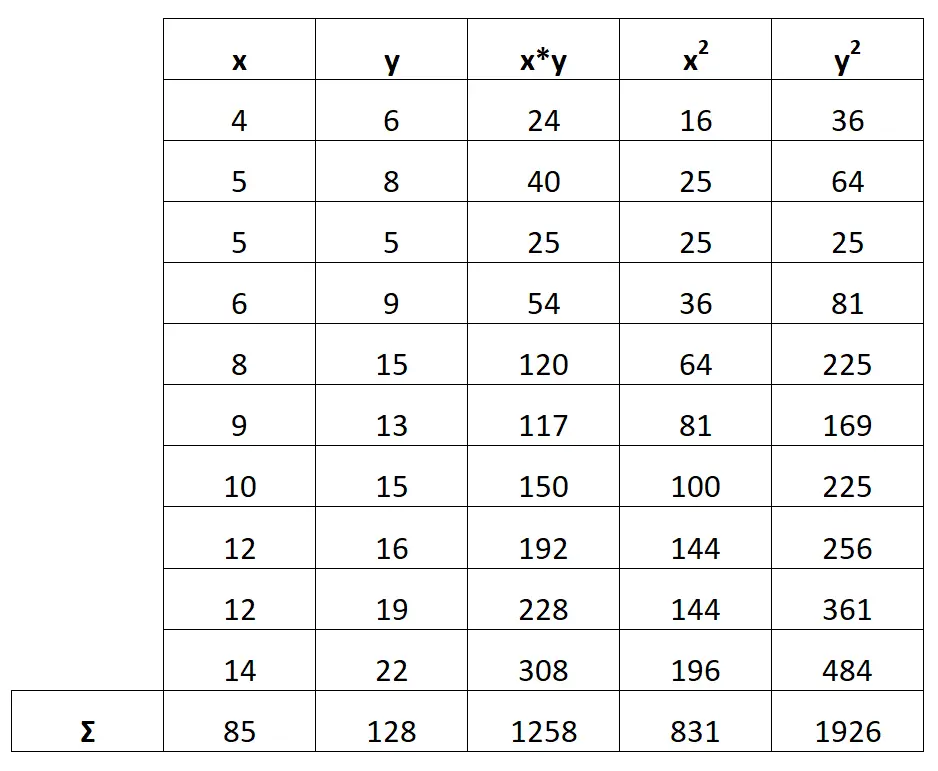
အဆင့် 3- b ₀ ကို တွက်ချက်ပါ။

ဆုတ်ယုတ်မှုညီမျှခြင်း၏ ကြားဖြတ်ကို တွက်ချက်ရန်အတွက် ဖော်မြူလာမှာ b ₀ ဖြစ်သည်၊

• b ₀ = ((Σy)(Σx ² ) – (Σx)(Σxy)) / (n(Σx ² ) – (Σx) ² )
• b ₀ = ((128)(831) – (85)(1258)) / (10(831) – (85) ² )
• _b0 = -0.518

မှတ်ချက် – ဖော်မြူလာတွင်၊ n သည် လေ့လာတွေ့ရှိချက်စုစုပေါင်းကို ကိုယ်စားပြုသည်။ ဤဥပမာတွင်၊ စုစုပေါင်းရှုမြင်ချက် ၁၀ ခုရှိသည်။

အဆင့် 4- b ₁ ကို တွက်ချက်ပါ။

regression equation ၏ slope ကို တွက်ချက်ရန် ဖော်မြူလာ b ₁ ၊

• b ₁ = (n(Σxy) – (Σx)(Σy)) / (n(Σx ² ) – (Σx) ² )
• b ₁ = (10(1258) – (85)(128)) / (10(831) – (85) ² )
• _b1 = 1.5668

အဆင့် 5- linear regression equation ကိုရေးပါ။

နောက်ဆုံး linear regression equation ကို အောက်ပါအတိုင်း ရေးသားနိုင်ပါသည်။

• ŷ = b ₀ + b ₁ x

ထို့ကြောင့် ကျွန်ုပ်တို့၏ linear regression equation ကို အောက်ပါအတိုင်း ရေးသားထားမည်ဖြစ်ပါသည်။

• ŷ = -0.518 + 1.5668x

ရိုးရှင်းသော linear regression calculator တွင် ဇယားမှ တန်ဖိုးများကို ချိတ်ဆက်ခြင်းဖြင့် ဤအဖြေသည် မှန်ကန်ကြောင်း ကျွန်ုပ်တို့ အတည်ပြုနိုင်သည်-

ဂဏန်းပေါင်းစက်မှ linear regression equation သည် ကျွန်ုပ်တို့ကိုယ်တိုင်တွက်ချက်ထားသော တစ်ခုနှင့် ကိုက်ညီကြောင်း ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် linear regression နှင့်ပတ်သက်သော နောက်ထပ်အချက်အလက်များကို ပေးဆောင်သည်-

Simple Linear Regression နိဒါန်း
Multiple Linear Regression အကြောင်း နိဒါန်း
regression coefficient ကို ဘယ်လိုအဓိပ္ပာယ်ဖွင့်မလဲ။