အတိုင်းအတာတစ်ခုနှင့် တည်နေရာပြကွက်ကို အဓိပ္ပါယ်ဖွင့်ဆိုပုံ- ဥပမာများဖြင့်

အတိုင်းအတာသတ်မှတ်ထားသော တည်နေရာဇယား သည် x-ဝင်ရိုးတစ်လျှောက်နှင့် y-ဝင်ရိုးတစ်လျှောက် စံသတ်မှတ်ထားသော ကျန်ရှိနေသော အကြွင်းအကျန်များ၏ နှစ်ထပ် ကိန်းတန်ဖိုးများကို ပြသသည့် ဇယားအမျိုးအစားတစ်ခုဖြစ်သည်။

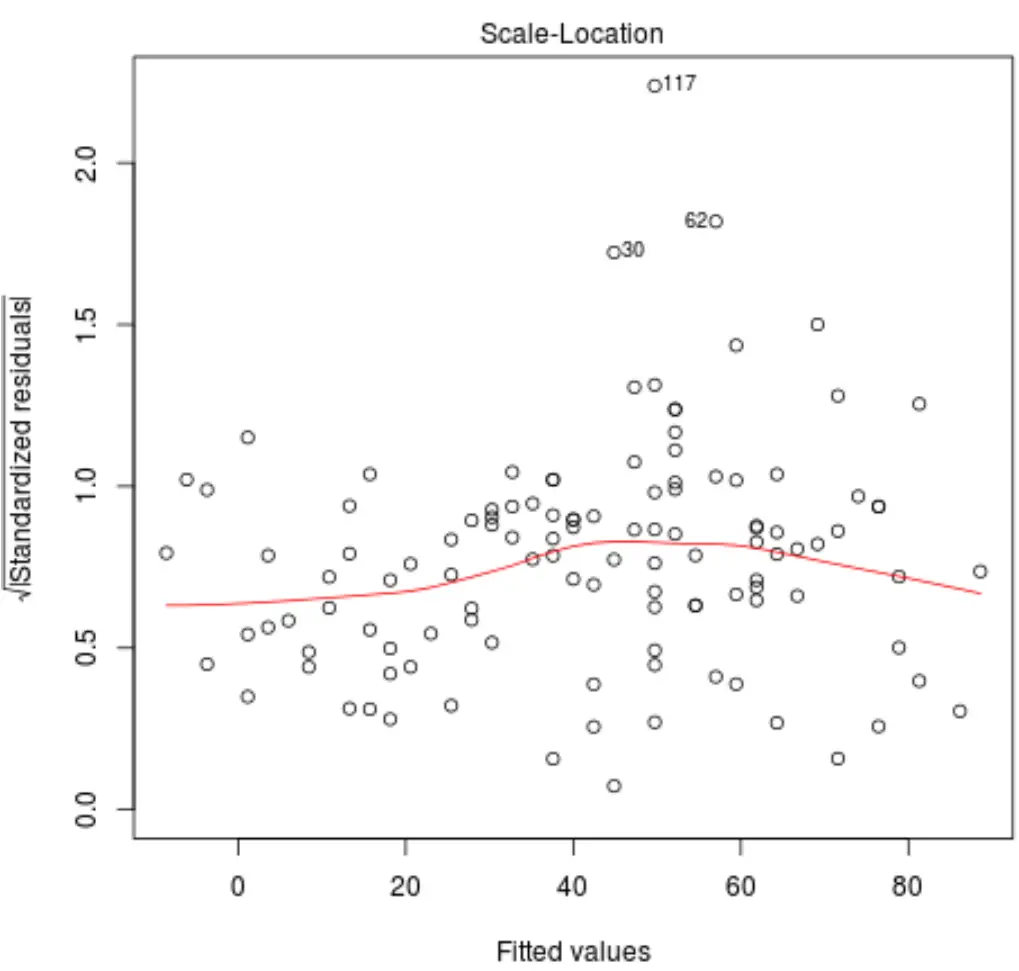
ဤဂရပ်ကိုကြည့်လျှင် ကျွန်ုပ်တို့သည် အရာနှစ်ခုကို စစ်ဆေးသည်-

1. အနီရောင်မျဉ်းသည် ကွက်ကွက်ပေါ်တွင် ခန့်မှန်းခြေ အလျားလိုက်ဖြစ်နေကြောင်း စစ်ဆေးပါ။ ဤသို့ဆိုလျှင်၊ တူညီသောယူဆချက် သည် ပေးထားသော ဆုတ်ယုတ်မှုပုံစံအတွက် ကျေနပ်ဖွယ်ဖြစ်သည်။ ဆိုလိုသည်မှာ၊ အကြွင်းအကျန်များ ဖြန့်ဖြူးမှုသည် တပ်ဆင်တန်ဖိုးအားလုံးအတွက် ခန့်မှန်းခြေအားဖြင့် တူညီပါသည်။

2. အကြွင်းအကျန်များကြားတွင် ရှင်းလင်းပြတ်သားသော လမ်းကြောင်းမရှိကြောင်း စစ်ဆေးပါ။ တစ်နည်းဆိုရသော်၊ တပ်ဆင်ထားသောတန်ဖိုးများအားလုံးအတွက် အနီးစပ်ဆုံးတူညီသောကွဲပြားမှုဖြင့် အကြွင်းအကျန်များကို အနီရောင်မျဉ်းတစ်ဝိုက်တွင် ကျပန်းဖြန့်ကျဲသင့်သည်။

R တွင် စကေးနှင့် တည်နေရာ ကွက်ကွက်များ

R တွင် ရိုးရှင်းသော မျဉ်းဖြောင့်ဆုတ်ယုတ်မှုပုံစံကို အံဝင်ခွင်ကျဖြစ်စေရန် အောက်ပါကုဒ်ကို အသုံးပြုနိုင်ပြီး ရလဒ်မော်ဒယ်အတွက် စကေးနှင့် တည်နေရာကွက်ကွက်ကို ထုတ်လုပ်နိုင်သည်-

 #fit simple linear regression model
model <- lm(Ozone ~ Temp, data = airquality)

#produce scale-location plot
plot(model)

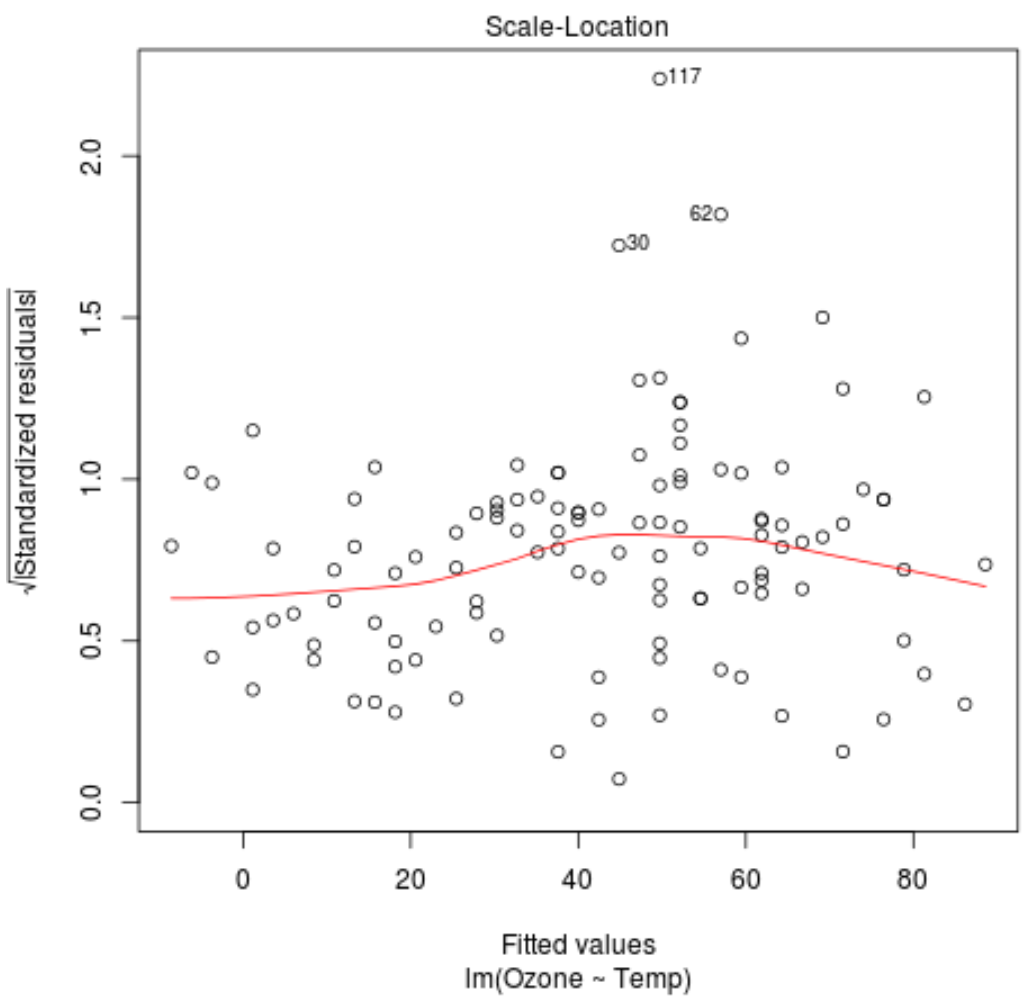
ဤဆုတ်ယုတ်မှုပုံစံ၏ စကေး-တည်နေရာကွက်ကွက်မှ အောက်ပါအရာနှစ်ခုကို ကျွန်ုပ်တို့ သတိပြုနိုင်သည်။

1. အနီရောင်မျဉ်းသည် ကွက်ကွက်ပေါ်တွင် ခန့်မှန်းခြေအားဖြင့် အလျားလိုက်ဖြစ်သည်။ ဤသို့ဆိုလျှင်၊ ပေးထားသော ဆုတ်ယုတ်မှုပုံစံအတွက် တူညီသော ယူဆချက် သည် ကျေနပ်ပါသည်။ ဆိုလိုသည်မှာ၊ အကြွင်းအကျန်များ ဖြန့်ဖြူးမှုသည် တပ်ဆင်တန်ဖိုးအားလုံးအတွက် ခန့်မှန်းခြေအားဖြင့် တူညီပါသည်။

2. အကြွင်းအကျန်များကြားတွင် ရှင်းလင်းပြတ်သားသော လမ်းကြောင်းမရှိကြောင်း စစ်ဆေးပါ။ တစ်နည်းဆိုရသော်၊ တပ်ဆင်ထားသောတန်ဖိုးများအားလုံးအတွက် အနီးစပ်ဆုံးတူညီသောကွဲပြားမှုဖြင့် အကြွင်းအကျန်များကို အနီရောင်မျဉ်းတစ်ဝိုက်တွင် ကျပန်းဖြန့်ကျဲသင့်သည်။

နည်းပညာမှတ်စုများ

စံချိန်စံညွှန်းသတ်မှတ်ထားသော အကြွင်းအကျန်များရှိသည့် ဒေတာအတွဲမှ လေ့လာတွေ့ရှိချက်သုံးခုကို ဂရပ်တွင် တံဆိပ်တပ်ထားသည်။

စာကြောင်း 30၊ 62 နှင့် 117 တွင် လေ့လာတွေ့ရှိချက်များတွင် အမြင့်ဆုံး စံသတ်မှတ်ထားသော အကြွင်းအကျန်များ ရှိနေသည်ကို ကျွန်ုပ်တို့ တွေ့နိုင်ပါသည်။

ဤလေ့လာတွေ့ရှိချက်များသည် လွန်ကဲသည်ဟု မဆိုလိုပါ၊ သို့သော် ဤလေ့လာတွေ့ရှိချက်များကို ပိုမိုနီးကပ်စွာစစ်ဆေးရန် မူရင်းဒေတာကို သင်ကြည့်ရှုလိုပေမည်။

အနီရောင်မျဉ်းသည် စကေးတည်နေရာပြကွက်တွင် အကြမ်းဖျင်းအားဖြင့် အလျားလိုက်ဖြစ်ကြောင်း ကျွန်ုပ်တို့မြင်နိုင်သော်လည်း၊ ယင်းသည် လိင်တူဆက်ဆံခြင်း၏ ယူဆချက်အား ကျေနပ်မှုရှိမရှိ ကြည့်ရှုရန် အမြင်သာနည်းလမ်းတစ်ခုဖြစ်သည်။

လိင်တူဆက်ဆံခြင်း၏ ယူဆချက်သည် Breusch-Pagan စမ်းသပ်မှု ဖြစ်သည်ကို သိရှိရန် ကျွန်ုပ်တို့အသုံးပြုနိုင်သည့် တရားဝင်ကိန်းဂဏန်းစမ်းသပ်မှုတစ်ခုဖြစ်သည်။

Breusch-Pagan စမ်းသပ်မှု R

R တွင် Breusch-Pagan စမ်းသပ်မှုလုပ်ဆောင်ရန် အောက်ပါကုဒ်သည် lmtest ပက်ကေ့ဂျ်၏ bptest() လုပ်ဆောင်ချက်ကို မည်သို့အသုံးပြုရမည်ကို ပြသသည်-

 #load lmtest package
library(lmtest)

#perform Breusch-Pagan Test
bptest(model)

	studentized Breusch-Pagan test

data: model
BP = 1.4798, df = 1, p-value = 0.2238

Breusch-Pagan စမ်းသပ်မှုတစ်ခုသည် အောက်ပါ null နှင့် အခြားအခြားသော အယူအဆများကို အသုံးပြုသည်-

• Null hypothesis (H ₀ ) : အကြွင်းအကျန်များသည် homoscedastic (ဆိုလိုသည်မှာ တစ်ပြေးညီ ဖြန့်ဝေသည်)
• အစားထိုးယူဆချက် ( _HA ) : အကြွင်းအကျန်များသည် heteroskedastic (ဆိုလိုသည်မှာ တစ်ပြေးညီမဖြန့်ဝေပါ)

ရလဒ်မှ၊ စမ်းသပ်မှု၏ p-value သည် 0.2238 ဖြစ်သည်ကို ကျွန်ုပ်တို့တွေ့နိုင်သည်။ ဤ p-value သည် 0.05 ထက်မနည်းသောကြောင့်၊ null hypothesis ကို ငြင်းပယ်ရန် ပျက်ကွက်ပါသည်။ ဆုတ်ယုတ်မှုပုံစံတွင် heteroskedasticity ရှိနေသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထား မရှိပါ။

ဤရလဒ်သည် စကေးတည်နေရာကွက်လပ်ရှိ အနီရောင်မျဉ်းအား ကျွန်ုပ်တို့၏အမြင်အာရုံစစ်ဆေးခြင်းနှင့် ကိုက်ညီပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

Regression Analysis တွင် Heteroscedasticity ကို နားလည်ခြင်း။
R တွင်ကျန်ရှိသောကွက်ကွက်ဖန်တီးနည်း
R တွင် Breusch-Pagan စမ်းသပ်မှုပြုလုပ်နည်း