အကောင်းဆုံးအစုများကိုရှာဖွေရန် r တွင် elbow နည်းလမ်းကိုအသုံးပြုနည်း

machine learning တွင် အသုံးအများဆုံး အစုလိုက်အပြုံလိုက် အယ်လဂိုရီသမ်များထဲမှ တစ်ခုကို k-means clustering ဟုခေါ်သည်။

K ဆိုသည်မှာ အစုအဝေးတစ်ခုစီကို K အစုအဝေးတစ်ခုသို့ ဒေတာအတွဲတစ်ခုမှ စူးစမ်းလေ့လာမှုတစ်ခုစီကို ထားရှိပေးသည့် နည်းလမ်းတစ်ခုဖြစ်သည်။

အဆုံးပန်းတိုင်မှာ အစုအဝေးတစ်ခုစီရှိ ရှုမြင်သုံးသပ်ချက်များသည် တစ်ခုနှင့်တစ်ခု အလွန်တူညီပြီး ကွဲပြားသောအစုအဝေးများတွင် လေ့လာမှုများသည် တစ်ခုနှင့်တစ်ခု အလွန်ကွာခြားသော်လည်း K အစုအဝေးများ ရှိရန်ဖြစ်သည်။

k-means အစုအဝေးပြုလုပ်သောအခါ၊ ပထမအဆင့်မှာ ကျွန်ုပ်တို့လေ့လာသုံးသပ်ချက်ထည့်လိုသောအစုအဝေးအရေအတွက် K အတွက်တန်ဖိုးကိုရွေးချယ်ရန်ဖြစ်သည်။

K အတွက် တန်ဖိုးတစ်ခုကို ရွေးချယ်ရန် အသုံးအများဆုံးနည်းလမ်းများထဲမှ တစ်ခုကို elbow method ဟုခေါ်သည် ၊ x-axis ပေါ်ရှိ အစုအစည်းများ၏ အရေအတွက်နှင့် y-ဝင်ရိုးပေါ်ရှိ စတုရန်းနှစ်ခုပေါင်း၏ စုစုပေါင်း ကွက်ကွက်ဖန်တီးခြင်း ပါဝင်သည့် elbow method ဟုခေါ်သည်၊ ထို့နောက် ခွဲခြားသတ်မှတ်ပါ။ “ ဒူး” သို့မဟုတ် အလှည့်တစ်ခုသည် ကွက်ကွက်ထဲတွင် ပေါ်လာသည်။

“ဒူး” ဖြစ်ပေါ်လာသည့် x ဝင်ရိုးပေါ်ရှိ အမှတ်သည် k-ဆိုလိုသည် အစုလိုက်အပြုံလိုက် အယ်လဂိုရီသမ်တွင် အသုံးပြုရန် အကောင်းဆုံး အစုအဝေးအရေအတွက်ကို ပြောပြသည်။

အောက်ဖော်ပြပါ ဥပမာသည် R တွင် တံတောင်ဆစ်နည်းလမ်းကို အသုံးပြုနည်းကို ပြသထားသည်။

ဥပမာ- R တွင် Elbow Method ကိုအသုံးပြုခြင်း။

ဤဥပမာအတွက်၊ ကျွန်ုပ်တို့သည် လူသတ်မှု၊ ချေမှုန်းရေးနှင့် မုဒိမ်းမှုများအတွက် 1973 ခုနှစ်တွင် အမေရိကန်ပြည်နယ်တစ်ခုစီရှိ လူ 100,000 တစ်ဦးလျှင် ဖမ်းဆီးခံရမှု အရေအတွက်ပါဝင်သည့် R တွင်တည်ဆောက်ထားသော USArrests ဒေတာအစုံကို အသုံးပြုမည်ဖြစ်ပြီး မြို့ပြတွင်နေထိုင်သော ပြည်နယ်တစ်ခုစီ၏ လူဦးရေရာခိုင်နှုန်း ဒေသများ။ , UrbanPop ။

အောက်ပါကုဒ်သည် ဒေတာအတွဲကို မည်သို့တင်ရမည်၊ ပျောက်နေသောတန်ဖိုးများပါရှိသော အတန်းများကို ဖယ်ရှားရန်နှင့် 0 ၏ပျမ်းမျှနှင့် 1 စံသွေဖည်မှုရှိရန် ဒေတာအတွဲရှိ variable တစ်ခုစီကို အတိုင်းအတာတစ်ခုစီကို ပြသသည်-

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

k-means algorithm တွင် အသုံးပြုရန် အကောင်းဆုံး အစုအဝေး အရေအတွက်ကို ရှာရန်၊ ကျွန်ုပ်တို့သည် စတုရန်း၏ ပေါင်းလဒ်နှင့် စုစုပေါင်း၏ အစုအဝေး၏ အရေအတွက်ကို ဖန်တီးရန်အတွက် factoextra ပက်ကေ့ဂျ်မှ fviz_nbclust() လုပ်ဆောင်ချက်ကို အသုံးပြုပါမည်။

 library (cluster)
library (factoextra)

#create plot of number of clusters vs total within sum of squares
fviz_nbclust(df, kmeans, method = “ wss ”) 

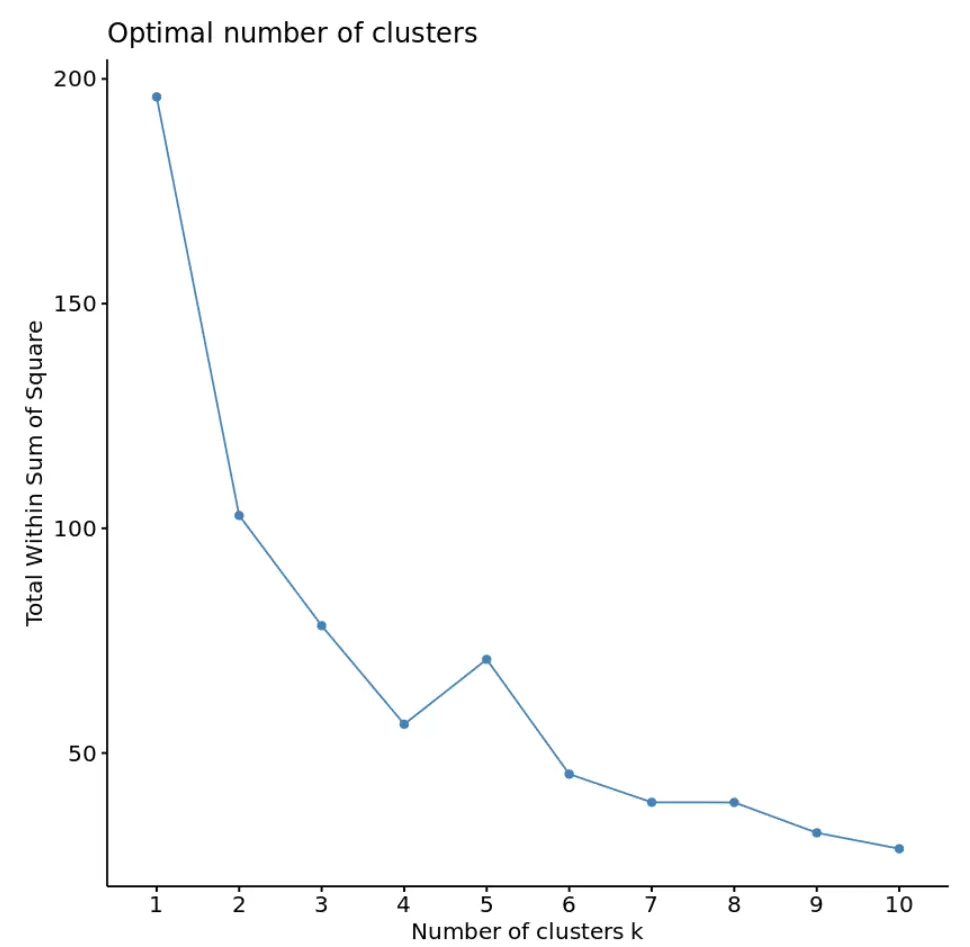
ဤဂရပ်တွင်၊ “ ဒူး” သို့မဟုတ် k = 4 အစုအဝေးတွင် kink ရှိနေပုံပေါ်သည်။ ဤသည်မှာ စတုရန်းများ ပေါင်းလဒ်များ တည်ငြိမ်စပြုသည့် အချက်ဖြစ်သည်။

k-means algorithm တွင် အသုံးပြုရန် အကောင်းဆုံး အစုအဝေး အရေအတွက်သည် 4 ဖြစ်ကြောင်း ၎င်းက ကျွန်ုပ်တို့အား ပြောပြသည်။

မှတ်ချက် – အစုအဝေးများကိုအသုံးပြုခြင်းဖြင့် စတုရန်း၏ပေါင်းလဒ်တွင် စုစုပေါင်းနည်းနိုင်သော်လည်း၊ ကျွန်ုပ်တို့သည် လေ့ကျင့်ရေးဒေတာကို ပိုအံကိုက်ဖြစ်နိုင်သော ကြောင့် k-means algorithm သည် စမ်းသပ်ဒေတာတွင်လည်း အလုပ်မဖြစ်နိုင်ပါ။

k -4 ၏ အကောင်းဆုံးတန်ဖိုးကို အသုံးပြု၍ ဒေတာအတွဲပေါ်တွင် k-means အစုအဝေးကို လုပ်ဆောင်ရန် အစု အဝေးမှ kmeans() လုပ်ဆောင်ချက်ကို အသုံးပြုနိုင်သည်။

 #make this example reproducible
set. seeds (1)

#perform k-means clustering with k = 4 clusters
km <- kmeans(df, centers = 4, nstart = 25)

#view results
km

K-means clustering with 4 clusters of sizes 16, 13, 13, 8

Cluster means:
      Murder Assault UrbanPop Rape
1 -0.4894375 -0.3826001 0.5758298 -0.26165379
2 -0.9615407 -1.1066010 -0.9301069 -0.96676331
3 0.6950701 1.0394414 0.7226370 1.27693964
4 1.4118898 0.8743346 -0.8145211 0.01927104

Vector clustering:
       Alabama Alaska Arizona Arkansas California Colorado 
             4 3 3 4 3 3 
   Connecticut Delaware Florida Georgia Hawaii Idaho 
             1 1 3 4 1 2 
      Illinois Indiana Iowa Kansas Kentucky Louisiana 
             3 1 2 1 2 4 
         Maine Maryland Massachusetts Michigan Minnesota Mississippi 
             2 3 1 3 2 4 
      Missouri Montana Nebraska Nevada New Hampshire New Jersey 
             3 2 2 3 2 1 
    New Mexico New York North Carolina North Dakota Ohio Oklahoma 
             3 3 4 2 1 1 
        Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 
             1 1 1 4 2 4 
         Texas Utah Vermont Virginia Washington West Virginia 
             3 1 2 1 1 2 
     Wisconsin Wyoming 
             2 1 

Within cluster sum of squares by cluster:
[1] 16.212213 11.952463 19.922437 8.316061
 (between_SS / total_SS = 71.2%)

Available components:

[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss"   
[7] "size" "iter" "ifault"         

ရလဒ်များမှ ကျွန်ုပ်တို့ မြင်နိုင်သည်-

• ပြည်နယ် ၁၆ ခုကို ပထမအစုအဖွဲ့တွင် တာဝန်ပေးအပ်ခဲ့သည်။
• ပြည်နယ် 13 ခုကို ဒုတိယအစုအဖွဲ့တွင် တာဝန်ပေးအပ်ထားသည်။
• ပြည်နယ် 13 ခုကို တတိယအစုအဖွဲ့တွင် တာဝန်ပေးအပ်ထားသည်။
• စတုတ္ထအစုအဖွဲ့တွင် ပြည်နယ် ၈ ခုကို တာဝန်ပေးအပ်ထားသည်။

ပြည်နယ်တစ်ခုစီ၏ အစုအဖွဲ့တာဝန်များကို မူရင်းဒေတာအတွဲသို့လည်း ထည့်သွင်းနိုင်သည်-

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)

#view final data
head(final_data)

	Murder Assault UrbanPop Rape cluster
				
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

မူရင်းဒေတာဘေ့စ်မှ ရှုမြင်မှုတစ်ခုစီကို အုပ်စုလေးခုအနက်မှ တစ်ခုစီတွင် ထည့်သွင်းထားသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် R တွင် အမျိုးမျိုးသော အစုလိုက်အပြုံလိုက် အယ်လဂိုရီသမ်များကို မည်သို့လုပ်ဆောင်ရမည်ကို အဆင့်ဆင့် ဥပမာပေးထားပါသည်။

R တွင် K-Means Clustering- အဆင့်ဆင့် ဥပမာ
R တွင် K-Medoids Clustering- အဆင့်ဆင့် ဥပမာ
R တွင် အဆင့်ဆင့်သော အစုအဝေးများ