တြိဂံဖြန့်ချီခြင်းအကြောင်း မိတ်ဆက်

တြိဂံပုံသဏ္ဍာန်ဖြန့်ဝေမှုသည် တြိဂံပုံသဏ္ဍာန်ဖြစ်နိုင်ခြေသိပ်သည်းဆလုပ်ဆောင်မှုဖြင့် စဉ်ဆက်မပြတ်ဖြစ်နိုင်ခြေဖြန့်ဝေမှုတစ်ခုဖြစ်သည်။

၎င်းကို တန်ဖိုးသုံးခုဖြင့် သတ်မှတ်သည်။

• အနိမ့်ဆုံး တန်ဖိုးရှိတယ်။
• အမြင့်ဆုံးတန်ဖိုး b
• အမြင့်ဆုံးတန်ဖိုး c

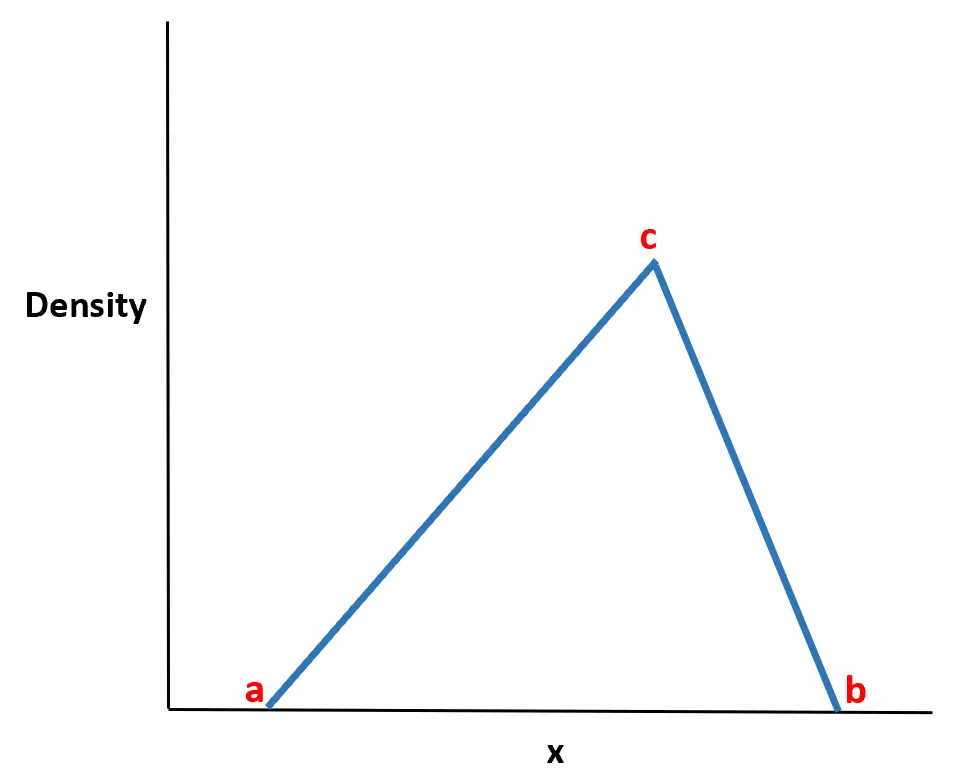
ဖြန့်ဖြူးမှု၏အမည်သည် ဖြစ်နိုင်ခြေသိပ်သည်းဆလုပ်ဆောင်မှုတွင် တြိဂံပုံသဏ္ဍာန်ရှိသည်ဟူသောအချက်မှ ဆင်းသက်လာခြင်းဖြစ်သည်။

ကျွန်ုပ်တို့သည် မကြာခဏဆိုသလို အနိမ့်ဆုံးတန်ဖိုး (a)၊ အမြင့်ဆုံးတန်ဖိုး (b) နှင့် ကျပန်းပြောင်းလဲ နိုင်သော ဖြစ်နိုင်ခြေအရှိဆုံးတန်ဖိုး (c) ကို ခန့်မှန်းနိုင်သောကြောင့် ဤဖြန့်ဖြူးမှုသည် လက်တွေ့ကမ္ဘာတွင် အလွန်အသုံးဝင်ကြောင်း ထွက်ပေါ်လာပါသည်။ ဤတန်ဖိုးသုံးခုကိုသာသိသော တြိဂံဖြန့်ဝေမှုကို အသုံးပြု၍ ကျပန်းကိန်းရှင်များ၏ အပြုအမူကို မကြာခဏ စံနမူနာပြုနိုင်သည်။

ဥပမာအားဖြင့်၊ စားသောက်ဆိုင်တစ်ဆိုင်သည် လာမည့်သီတင်းပတ်အတွက် ၎င်း၏စုစုပေါင်းရောင်းအားသည် အနည်းဆုံး $10,000၊ အများဆုံး $30,000 နှင့် အများဆုံး $25,000 ဖြစ်လိမ့်မည်ဟု ခန့်မှန်းနိုင်သည်။

ဤနံပါတ်သုံးခုကို အသုံးပြု၍ အချို့သောအရောင်းအ၀ယ်ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ရန် တြိဂံပုံဖြန့်ဝေမှုကို အသုံးပြုနိုင်သည်။

တြိဂံဖြန့်ချီခြင်း၏ ဂုဏ်သတ္တိများ

တြိဂံပုံဖြန့်ဝေမှုတွင် အောက်ပါဂုဏ်သတ္တိများ ရှိသည်။

PDF-

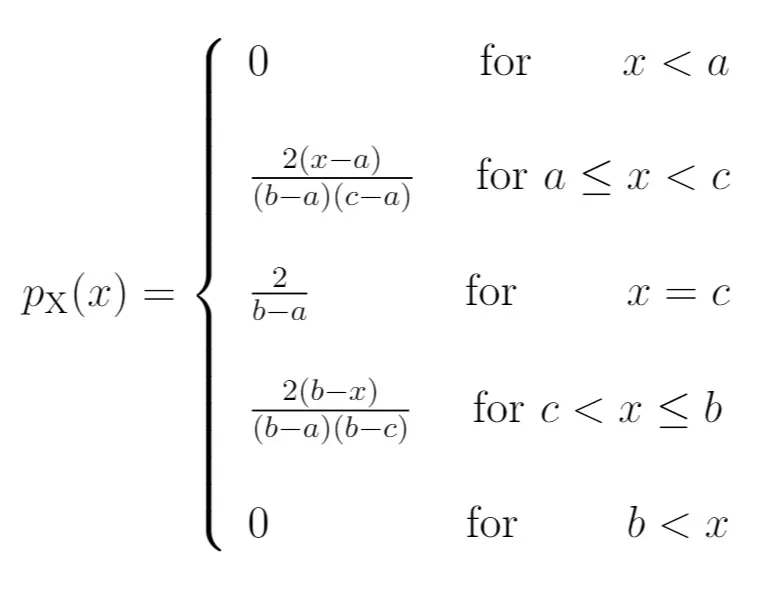
CDF-

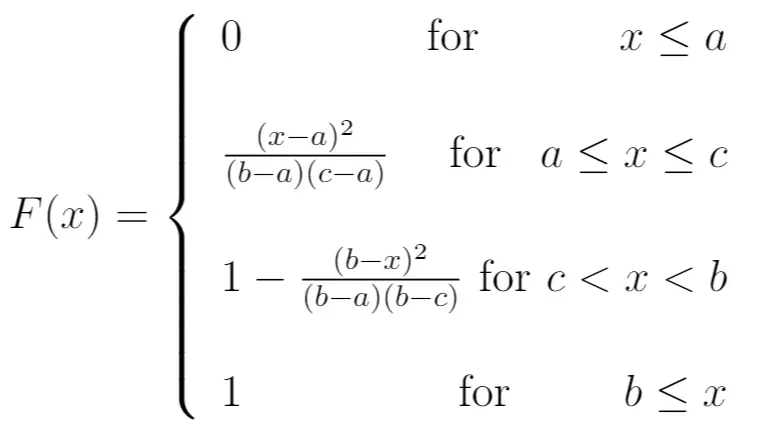
ပျမ်းမျှ: (a + b + c) / 3

မုဒ်: ဂ

ကွဲလွဲမှု- (a ² + b ² + c ² – ab – ac – bc) / 18

တြိဂံဖြန့်ဝေမှုကို အသုံးပြုခြင်း ဥပမာ

အရင် ဥပမာကို ပြန်သွားကြည့်ရအောင်။ စားသောက်ဆိုင်တစ်ဆိုင်သည် လာမည့်အပတ်အတွက် စုစုပေါင်းရောင်းချရမှုမှာ အနည်းဆုံး $10,000၊ အများဆုံး $30,000 နှင့် အများဆုံး $25,000 ဖြစ်လိမ့်မည်ဟု ခန့်မှန်းဆိုကြပါစို့။

စားသောက်ဆိုင်တွင် စုစုပေါင်းရောင်းအား $20,000 အောက် ဖြစ်နိုင်ချေရှိသနည်း။

ဤမေးခွန်းကိုဖြေဆိုရန်၊ ကျွန်ုပ်တို့သည် x = စုစုပေါင်းရောင်းအားကို မေးနိုင်ပါသည်။ x သည် အ နိမ့်ဆုံးတန်ဖိုး $10,000 နှင့် အမြင့်ဆုံးတန်ဖိုး c $25,000 ကြားတွင် ရှိနေသည်ကို ကျွန်ုပ်တို့သိပါသည်။

ထို့ကြောင့်၊ PDF အရ၊ စားသောက်ဆိုင်တွင် စုစုပေါင်းရောင်းချမှုတွင် $20,000 ထက်နည်းသော ဖြစ်နိုင်ခြေကို ရှာဖွေရန် အောက်ပါညီမျှခြင်းကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည်။

• P(X <$20,000) = (xa) ² /(ba)(ca))
• P(X <$20,000) = (20,000-10,000) ² /((30,000-10,000)(25,000-10,000))
• P(X <$20,000) = 0.333

စားသောက်ဆိုင်တွင် စုစုပေါင်းရောင်းအား $20,000 အောက်ရှိနိုင်ခြေမှာ 0.333 ဖြစ်သည်။

စားသောက်ဆိုင်အတွက် ပျမ်းမျှရောင်းအားက ဘယ်လောက်လဲ။

ယခင်ကပေးထားသော ပျမ်းမျှအတွက် ဖော်မြူလာကို အသုံးပြု၍ မျှော်လင့်ထားသော ပျမ်းမျှရောင်းအားကို တွက်ချက်နိုင်သည်-

• ပျမ်းမျှ = (a+b+c)/3
• ပျမ်းမျှ = ($10,000 + $30,000 + $25,000) / 3
• ပျမ်းမျှ = $21,667

ပျမ်းမျှရောင်းအားမှာ 21,667 ဖြစ်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် အခြားအသုံးများသော ဖြန့်ဝေမှုများကို မိတ်ဆက်ပေးသည်-

ပုံမှန် ဖြန့်ဖြူးမှု
binomial ဖြန့်ဖြူးမှု
ငါးဖြန့်ဖြူးရေး
ဂျီဩမေတြီ ဖြန့်ဖြူးမှု