Stata တွင် ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်နည်း

Logistic regression သည် တုံ့ပြန်မှု variable binary ဖြစ်သောအခါ regression model နှင့်ကိုက်ညီရန် ကျွန်ုပ်တို့အသုံးပြုသည့်နည်းလမ်းတစ်ခုဖြစ်သည်။ ဤသည်မှာ logistic regression ကိုအသုံးပြုခြင်း၏ဥပမာအချို့ဖြစ်သည်။

• လေ့ကျင့်ခန်း၊ အစားအသောက်နဲ့ ကိုယ်အလေးချိန်က နှလုံးရောဂါဖြစ်နိုင်ခြေကို ဘယ်လိုသက်ရောက်မှုရှိလဲ သိချင်ပါတယ်။ တုံ့ပြန်မှုပုံစံသည် နှလုံးဖောက်ပြန်ခြင်း ဖြစ်ပြီး ၎င်းတွင် ဖြစ်နိုင်ချေရလဒ် နှစ်ခုရှိသည်။
• GPA၊ ACT ရမှတ်နှင့် AP သင်တန်းများ အများအပြားသည် တက္ကသိုလ်တစ်ခုသို့ လက်ခံခြင်းဖြစ်နိုင်ခြေကို မည်သို့အကျိုးသက်ရောက်သည်ကို ကျွန်ုပ်တို့ သိရှိလိုပါသည်။ တုံ့ပြန်မှု ကိန်းရှင်သည် လက်ခံခြင်းဖြစ်ပြီး ၎င်းတွင် ဖြစ်နိုင်ချေရှိသော ရလဒ်နှစ်ခု ရှိသည်- လက်ခံသည် သို့မဟုတ် လက်မခံပါ။
• စကားလုံးအရေအတွက်နှင့် အီးမေးလ်ခေါင်းစဉ်သည် အီးမေးလ်တစ်ခုစပမ်းဖြစ်နိုင်ချေကို သက်ရောက်မှုရှိမရှိ သိလိုပါသည်။ တုံ့ပြန်မှုပုံစံသည် စပမ်း ဖြစ်ပြီး ၎င်းတွင် ဖြစ်နိုင်ချေရှိသော ရလဒ်နှစ်ခုရှိသည်- spam သို့မဟုတ် spam မဟုတ်ပေ။

ဤသင်ခန်းစာသည် Stata ရှိ ထောက်ပံ့ပို့ဆောင်ရေးဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။

ဥပမာ- Stata ရှိ ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှု

မိခင်၏အသက်အရွယ်နှင့် ဆေးလိပ်သောက်ခြင်းအလေ့အထများသည် မွေးကင်းစကိုယ်အလေးချိန်နည်းသော ကလေးမွေးဖွားနိုင်ခြေကို သက်ရောက်မှုရှိမရှိ နားလည်လိုသည်ဆိုပါစို့။

၎င်းကိုလေ့လာရန်၊ ကျွန်ုပ်တို့သည် အသက်အရွယ်နှင့် ဆေးလိပ်သောက်ခြင်း (ဟုတ် သို့မဟုတ် မဟုတ်ဘူး) ကို တုံ့ပြန်မှုကိန်းရှင်အဖြစ် အသုံးပြု၍ ထောက်ပံ့ပို့ဆောင်ရေးဆုတ်ယုတ်မှုကို လုပ်ဆောင်နိုင်သည်။ တုံ့ပြန်မှု variable သည် binary ဖြစ်ပြီး ဖြစ်နိုင်ချေ ရလဒ် နှစ်ခုသာ ရှိသောကြောင့် – logistic regression ကို အသုံးပြုသင့်သည်။

မတူညီသောမိခင် 189 ခုတွင် ဒေတာပါရှိသော lbw ဟုခေါ်သော ဒေတာအတွဲကို အသုံးပြု၍ ထောက်ပံ့ပို့ဆောင်မှုဆုတ်ယုတ်မှုလုပ်ဆောင်ရန် Stata တွင် အောက်ပါအဆင့်များကို ပြီးအောင်လုပ်ပါ။

အဆင့် 1: ဒေတာကို တင်ပါ။

command box တွင် အောက်ပါတို့ကို ရိုက်ထည့်ခြင်းဖြင့် ဒေတာကို တင်ပါ-

https://www.stata-press.com/data/r13/lbw ကို အသုံးပြုပါ။

အဆင့် 2- ဒေတာအကျဉ်းချုပ်ကို ရယူပါ။

Command box တွင် အောက်ပါတို့ကို ရိုက်ထည့်ခြင်းဖြင့် သင်လုပ်ဆောင်နေသော ဒေတာကို လျင်မြန်စွာ နားလည်နိုင်သည်-

အကျဉ်းချုပ်ရန်

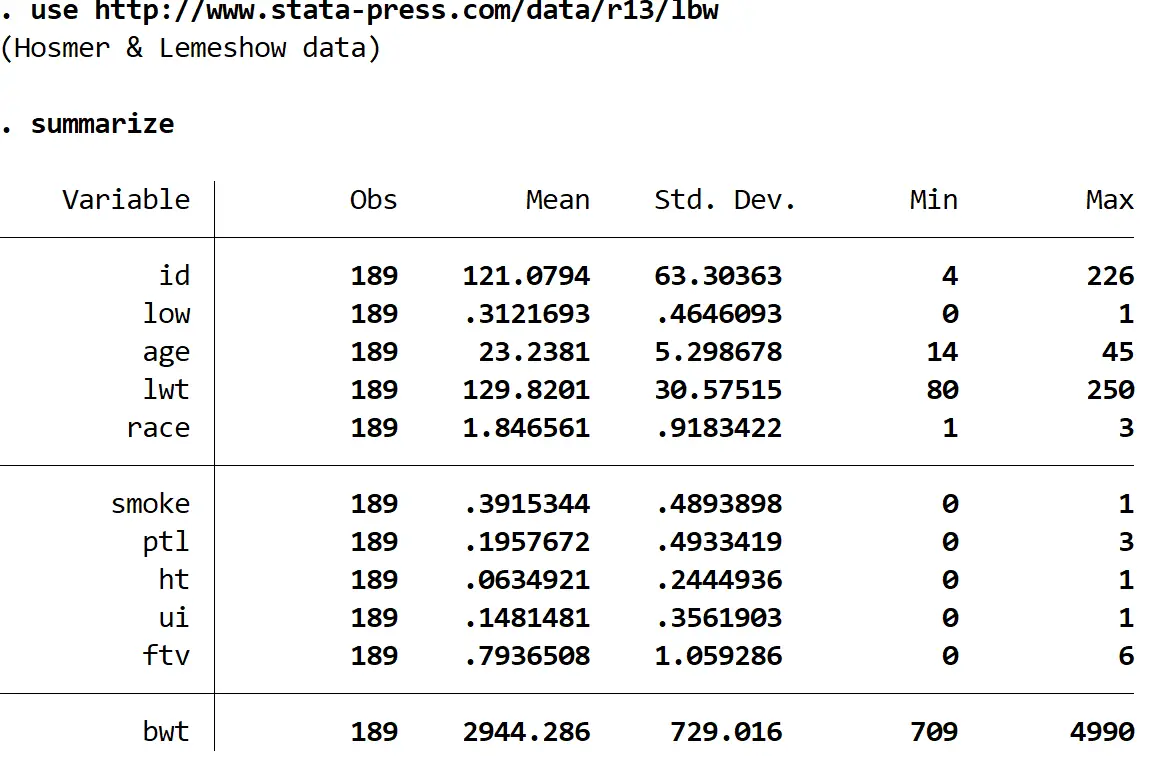
dataset တွင် မတူညီသော variable 11 ခုရှိသည်ကိုကျွန်ုပ်တို့တွေ့မြင်နိုင်သော်လည်းကျွန်ုပ်တို့စိတ်ဝင်စားသည့်တစ်ခုတည်းသောသုံးခုမှာ-

• နိမ့်ခြင်း – ကလေးမွေးပြီးချိန် ကိုယ်အလေးချိန် နည်းသည်ဖြစ်စေ မရှိသည်ဖြစ်စေ။ 1 = ဟုတ်၊ 0 = မရှိပါ။
• အသက် – မိခင်၏အသက်။
• ဆေးလိပ်သောက်ခြင်း – မိခင်သည် ကိုယ်ဝန်ဆောင်စဉ် ဆေးလိပ်သောက်သည်ဖြစ်စေ မသောက်သည်ဖြစ်စေ။ 1 = ဟုတ်၊ 0 = မရှိပါ။

အဆင့် 3- ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှုကို လုပ်ဆောင်ပါ။

အသက် နှင့် မီးခိုးများကို ရှင်းလင်းချက်ပြောင်းနိုင်သော ကိန်းရှင်များအဖြစ် အသုံးပြု၍ တုံ့ပြန်မှုကိန်းရှင်အဖြစ် နိမ့်ကျသော ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှုကို လုပ်ဆောင်ရန် အမိန့်ဘောက်စ်တွင် အောက်ပါတို့ကို ရိုက်ထည့်ပါ။

အသက်အရွယ်နိမ့်သော ဆေးလိပ်ငွေ့မှတ်တမ်း

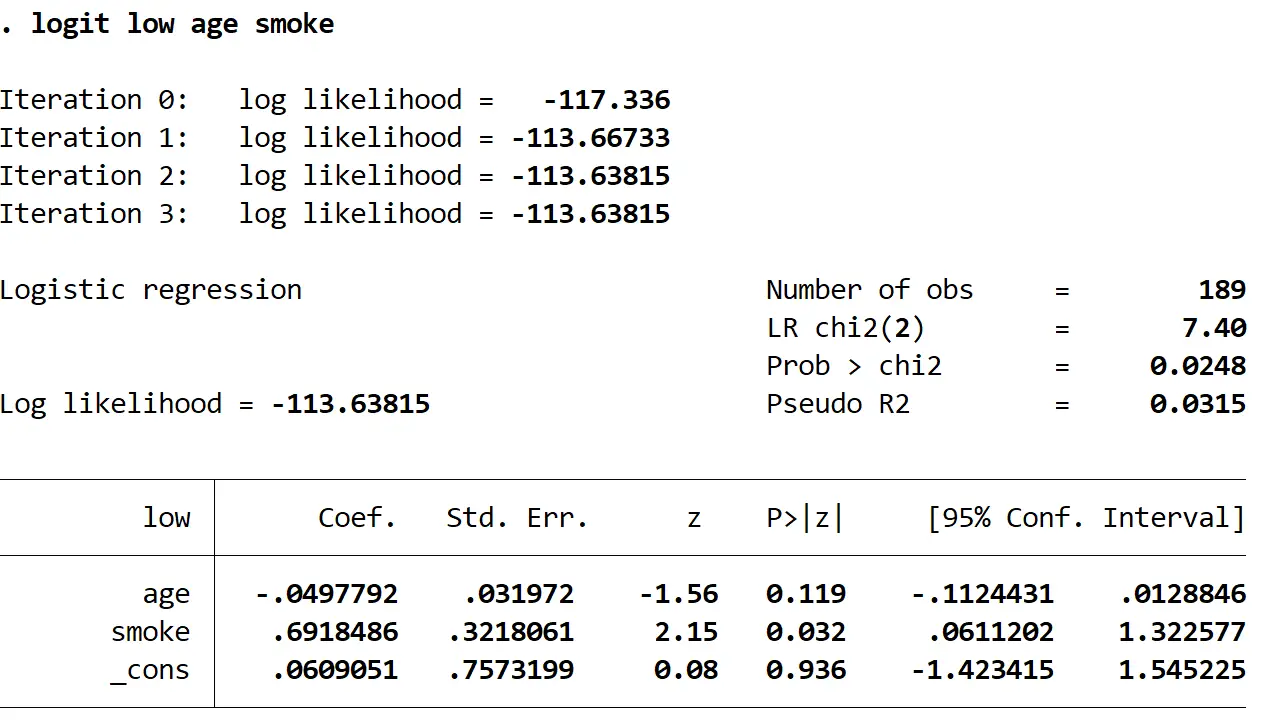
ရလဒ်တွင် စိတ်ဝင်စားစရာအကောင်းဆုံးဂဏန်းများကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံမှာ အောက်ပါအတိုင်းဖြစ်သည်။

Coef (အသက်) : -.0497792။ မီးခိုးငွေ့ကို အဆက်မပြတ် ကိုင်ဆောင်ထားခြင်းဖြင့် အသက်အရွယ် ကြီးလာမှု သည် နှစ်စဉ် exp(-0.0497792) = 0.951 နည်းပါးသော မွေးကင်းစကလေး ကိုယ်အလေးချိန် တိုးလာခြင်းနှင့် ဆက်စပ်နေသည်။ ဤကိန်းဂဏန်းသည် 1 ထက်နည်းသည်ဟု ဆိုလိုသည်မှာ အသက်အရွယ် တိုးလာခြင်းသည် ကိုယ်အလေးချိန်နည်းသော ကလေးမွေးဖွားနိုင်ခြေ လျော့နည်းခြင်းနှင့် ဆက်စပ်နေပါသည်။

ဥပမာ အမေ A နဲ့ အမေ B နှစ်ယောက်လုံး ဆေးလိပ်သောက်တယ် ဆိုပါစို့။ မိခင် A သည် မိခင် B ထက် တစ်နှစ်ပိုကြီးပါက မိခင် A သည် ကိုယ်အလေးချိန်နည်းသော ကလေးမွေးဖွားနိုင်ခြေ 95.1% သာရှိပြီး မိခင် B သည် ကိုယ်အလေးချိန်နည်းသော ကလေးမွေးဖွားနိုင်ခြေ၏ 95.1% သာရှိသည်။ မွေးဖွားခြင်း။

P>|z| (အသက်) : 0.119။ ၎င်းသည် အသက်အရွယ် အတွက် စမ်းသပ်မှုစာရင်းအင်းနှင့် ဆက်စပ်နေသည့် p-တန်ဖိုးဖြစ်သည်။ ဤတန်ဖိုးသည် 0.05 ထက်မနည်းသောကြောင့်၊ အသက်အရွယ်သည် မွေးရာပါကိုယ်အလေးချိန်နည်းပါးခြင်းအတွက် ကိန်းဂဏန်းအရ သိသာထင်ရှားသောခန့်မှန်းချက်မဟုတ်ပါ။

အလေးသာမှုအချိုး (မီးခိုး): 0.6918486။ ကိုယ်ဝန်ရှိစဉ် ဆေးလိပ်သောက်သောမိခင်သည် အသက်အရွယ်ကို ထိန်းထားနိုင်သည် exp.(6918486) = ကိုယ်ဝန်ရှိစဉ် ဆေးလိပ်မသောက်သောမိခင်ထက် ကိုယ်အလေးချိန်နည်းသော ကလေးမွေးဖွားခြင်း၏ 1.997 ဖြစ်နိုင်ခြေ ပိုများသည်။

ဥပမာ အမေ A နဲ့ အမေ B နှစ်ယောက်စလုံး အသက် 30 ဆိုပါစို့။ ကိုယ်ဝန်ဆောင်ကာလတွင် မိခင် A သည် ဆေးလိပ်သောက်ပြီး မိခင် B က ဆေးလိပ်မသောက်ပါက မိခင် A သည် ကိုယ်အလေးချိန်နည်းသော ကလေးမွေးဖွားနိုင်ခြေ 99.7% ထက် ပိုများသည်။

P>|z| (မီးခိုး) : 0.032 ။ ဤသည်မှာ မီးခိုး အတွက် စမ်းသပ်မှုစာရင်းအင်းနှင့် ဆက်စပ်နေသည့် p-တန်ဖိုးဖြစ်သည်။ ဤတန်ဖိုးသည် 0.05 ထက်နည်းသောကြောင့်၊ ဆေးလိပ်သောက်ခြင်းသည် မွေးကင်းစကိုယ်အလေးချိန်နည်းခြင်းအတွက် ကိန်းဂဏန်းအချက်အလတ်တစ်ခုဖြစ်သည်။

အဆင့် 4- ရလဒ်များကို သတင်းပို့ပါ။

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏ logistic regression ၏ရလဒ်များကို အစီရင်ခံလိုပါသည်။ ဤသည်မှာ ဤအရာကို ပြုလုပ်ပုံ၏ ဥပမာတစ်ခုဖြစ်သည်။

မိခင်၏အသက်အရွယ်နှင့် ဆေးလိပ်သောက်ခြင်းအလေ့အထသည် ကိုယ်အလေးချိန်နည်းသော ကလေးမွေးဖွားနိုင်ခြေကို သက်ရောက်မှုရှိမရှိ ဆုံးဖြတ်ရန် ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှုကို လုပ်ဆောင်ခဲ့သည်။ ခွဲခြမ်းစိတ်ဖြာမှုတွင် မိခင် ၁၈၉ ဦး၏ နမူနာကို အသုံးပြုခဲ့သည်။

ရလဒ်များက ဆေးလိပ်သောက်ခြင်းနှင့် ကိုယ်အလေးချိန်နည်းသော ကလေးမွေးဖွားနိုင်ခြေ (z = 2.15၊ p = 0.032) အကြား ကိန်းဂဏန်းအရ သိသာထင်ရှားသော ဆက်နွယ်မှု မရှိသော်လည်း အသက်အရွယ်နှင့် ကိုယ်အလေးချိန်နည်းခြင်း (z = -1.56) အကြား ကိန်းဂဏန်းအရ သိသာထင်ရှားသော ဆက်စပ်မှုရှိကြောင်း ပြသခဲ့သည်။ , p = 0.032) ။ ၁၁၉)။