ခြားနားချက်၏ ခွဲဝေမှု နမူနာကို ဆိုလိုသည်။
ဤဆောင်းပါးသည် ကိန်းဂဏန်းနှစ်ခုကြား ကွာခြားချက်၏နမူနာခွဲဝေမှုတွင် အဘယ်အရာဖြစ်သည်ကို ရှင်းပြထားသည်။ နည်းလမ်းများ၏ ခြားနားချက်ကိုနမူနာဖြန့်ဝေခြင်းအတွက် ဖော်မြူလာကို သင်တွေ့နိုင်မည်ဖြစ်ပြီး၊ ထို့အပြင် အဆင့်ဆင့်ဖြေရှင်းထားသော လေ့ကျင့်ခန်းတစ်ခုကိုလည်း သင်တွေ့လိမ့်မည်။
အဓိပ္ပါယ်ကွဲပြားမှု၏နမူနာဖြန့်ဝေမှုကား အဘယ်နည်း။
ကွဲပြားမှု၏နမူနာဖြန့်ဝေမှုသည် မတူညီသောလူဦးရေနှစ်ခုမှ ဖြစ်နိုင်သည့်နမူနာများအားလုံး၏နည်းလမ်းများကြား ကွာခြားချက်များကို တွက်ချက်ခြင်းမှ ထွက်ပေါ်လာသော ဖြန့်ဝေမှုဖြစ်သည်။
ဆိုလိုသည်မှာ၊ ဆိုလိုသည်မှာ ကွဲပြားမှု၏နမူနာခွဲဝေမှုကို ရယူရန်၊ လေ့လာမှုလူဦးရေနှစ်ခုမှ ဖြစ်နိုင်သည့်နမူနာအားလုံးကို ရွေးချယ်ရမည်ဖြစ်ပြီး၊ ထို့နောက် ရွေးချယ်ထားသော နမူနာတစ်ခုစီ၏ပျမ်းမျှအား တွက်ချက်ပြီး နောက်ဆုံးတွင် လူဦးရေနှစ်ခုမှ တွက်ချက်သော အဓိပ္ပါယ်အားလုံးအကြား ကွာခြားချက်ဖြစ်သည်။ ထို့ကြောင့် ဤလုပ်ငန်းဆောင်တာအားလုံး၏ အသုံးချပြီးနောက် ရရှိသော တန်ဖိုးများအစုသည် ကွဲပြားမှု၏နမူနာ ဖြန့်ဖြူးခြင်းကို ဆိုလိုသည်။

မတူညီသောလူဦးရေနှစ်ခု မှ ကျပန်းရွေးချယ်ထားသောနမူနာ နှစ်ခုကြားခြားနားချက်သည် လူဦးရေ၏ကွာခြားချက်နှင့်နီးစပ်သည်ဟုဖြစ်နိုင်ခြေကိုတွက်ချက်ရန် ကွာခြားချက်အားအသုံးပြုပါသည်။
ကွာခြားချက်၏နမူနာဖြန့်ဝေမှုအတွက် ဖော်မြူလာ
နမူနာအရွယ်အစားသည် အလုံအလောက်ကြီးနေပါက (n 1 ≥30 နှင့် n 2 ≥30)၊ ကွာခြားချက်၏နမူနာဖြန့်ဝေခြင်းဆိုသည်မှာ ပုံမှန်ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်သည်။ ပိုမိုတိကျစွာ၊ ပြောကြားထားသော ဖြန့်ဖြူးမှု၏ဘောင်များကို အောက်ပါအတိုင်း တွက်ချက်ပါသည်။
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-90c67b74b4e9326b7869d641a59725d9_l3.png)
မှတ်ချက်- လူဦးရေနှစ်မျိုးလုံးသည် ပုံမှန်ဖြန့်ဝေမှုများ ဖြစ်ပါက၊ ကွာခြားချက်၏နမူနာဖြန့်ဝေမှုသည် နမူနာအရွယ်အစားမခွဲခြားဘဲ ပုံမှန်ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်သည်။
ထို့ကြောင့်၊ ခြားနားချက်၏နမူနာခွဲဝေမှုကို သာမာန်ဖြန့်ဖြူးမှုဖြင့်သတ်မှတ်ထားသောကြောင့်၊ ဆိုလိုသည်မှာ ခြားနားချက်၏နမူနာဖြန့်ဝေမှု၏ ကိန်းဂဏန်းကို တွက်ချက်ရန်အတွက် ဖော်မြူလာ မှာ-

ရွှေ-
-

နမူနာ i ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
-

လူဦးရေရဲ့ ပျမ်းမျှ က i ပါ။
-

လူဦးရေ၏စံသွေဖည်မှု i။
-

နမူနာအရွယ်အစား i ဖြစ်ပါတယ်။
-

စံပုံမှန်ဖြန့်ဝေမှု N(0,1) မှသတ်မှတ်ထားသော ကိန်းရှင်တစ်ခုဖြစ်သည်။
မတူညီသောလူဦးရေမှနမူနာများတွင် မတူညီသောနမူနာအရွယ်အစားရှိနိုင်သည်ကို သတိပြုပါ။
ကွန်ကရစ်နမူနာ၏ ခြားနားချက်၏ နမူနာကို ဖြန့်ဖြူးခြင်းဟု ဆိုလိုသည်။
နမူနာဖြန့်ချီခြင်း၏ ခြားနားချက်၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ၎င်း၏ဖော်မြူလာသည် မည်ကဲ့သို့ဖြစ်သည်ကို ကျွန်ုပ်တို့မြင်သည်နှင့် တပြိုင်နက် နမူနာဖြန့်ဝေခြင်း၏ ခြားနားချက်၏ သဘောတရားကို နားလည်သဘောပေါက်ရန် အဆင့်ဆင့်နမူနာတစ်ခုကို ကျွန်ုပ်တို့တွေ့ရပါမည်။
- ကိန်းဂဏန်းလေ့လာမှုတစ်ခုတွင်၊ သတ်မှတ်ထားသောအသက်အရွယ်ရှိ ယောက်ျားလေးများနှင့် မိန်းကလေးများ၏ အရပ်အမြင့်ကွာခြားချက်ကို ခွဲခြမ်းစိတ်ဖြာလိုပါသည်။ ဤအသက်အရွယ် ယောက်ျားလေးများ၏ လူဦးရေကို သတ်မှတ်သည့် ဖြန့်ဖြူးမှုသည် ပျမ်းမျှ 157 စင်တီမီတာနှင့် စံသွေဖည်မှု 9 စင်တီမီတာရှိပြီး အခြားတစ်ဖက်တွင်၊ ဤအသက်အရွယ် မိန်းကလေးများ၏ လူဦးရေကို သတ်မှတ်သည့် ဖြန့်ဖြူးမှုသည် ပျမ်းမျှ 148 ရှိသည်။ စင်တီမီတာနှင့် စံသွေဖည် 7 စင်တီမီတာ။ ဒီအသက်အရွယ် ယောက်ျားလေး အယောက် 30 ရဲ့နမူနာနဲ့ ဒီအသက်အရွယ် မိန်းကလေး 35 ယောက်ရဲ့နမူနာကို ရွေးချယ်ခဲ့မယ်ဆိုရင် ယောက်ျားလေးတွေရဲ့ ပျမ်းမျှအရပ်ဟာ မိန်းကလေးနမူနာရဲ့ ပျမ်းမျှအရပ်အမြင့်ထက် 12 စင်တီမီတာ ပိုကြီးတဲ့ ဖြစ်နိုင်ခြေ ဘယ်လောက်ရှိလဲ။
ဤပြဿနာကိုဖြေရှင်းရန်၊ ပထမဆုံးလုပ်ရမည့်အရာမှာ နမူနာဖြန့်ချီခြင်း၏ ကွာခြားချက်၏ ကိန်းဂဏန်းကို တွက်ချက်ရန်ဖြစ်သည်။ ထို့ကြောင့် ကျွန်ုပ်တို့သည် အထက်ဖော်ပြပါ ပုံသေနည်းကို ကျင့်သုံးသည်-
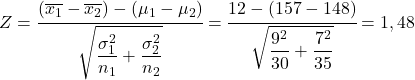
ထို့ကြောင့်၊ ယောက်ျားလေးများ၏ ပျမ်းမျှနမူနာအရပ်သည် မိန်းကလေးများ၏ ပျမ်းမျှအရပ်အမြင့်ထက် 12 စင်တီမီတာ ပိုများသောဖြစ်နိုင်ခြေသည် Z variable သည် 1.48 ထက်များသော ဖြစ်နိုင်ခြေနှင့် ညီမျှသည်။
![P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]” title=” Rendered by QuickLaTeX.com” height=” 19″ width=” 253″ style=” vertical-align: -5px;” ></p>
</p>
<p> ထို့ကြောင့် <a href=](https://statorials.org/wp-content/ql-cache/quicklatex.com-683cd2a72980115d8d18c906d619370a_l3.png) Z ၏ဇယား တွင် Z>1.48 ၏ဖြစ်နိုင်ခြေကိုရှာပါ :
Z ၏ဇယား တွင် Z>1.48 ၏ဖြစ်နိုင်ခြေကိုရှာပါ :
![P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]=0,0694″ title=” Rendered by QuickLaTeX.com” height=” 19″ width=” 331″ style=” vertical-align: -5px;” ></p>
</p>
<p> အတိုချုပ်ပြောရလျှင် ယောက်ျားလေးများ၏ ပျမ်းမျှအရပ်အမြင့်သည် မိန်းကလေးများ၏ ပျမ်းမျှအရပ်ထက် 12 စင်တီမီတာ ပိုများနိုင်ခြေမှာ 6.94% ဖြစ်သည်။</p>
</div><!-- End Content -->
<!-- Start Author Box -->
<div class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-5b83fdc11bd2320249679c4752660451_l3.png)
စာရေးသူအကြောင်း
Benjamin Anderson
မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။