နမူနာဖြန့်ချီခြင်း။
ဤဆောင်းပါးသည် ကိန်းဂဏန်းစာရင်းဇယားများတွင် မည်သည့်နမူနာဖြန့်ဖြူးမှုနှင့် ၎င်းကိုအသုံးပြုသည်ကို ရှင်းပြထားသည်။ ထို့ကြောင့် နမူနာဖြန့်ဝေမှု၏ အဓိပ္ပါယ်၊ နမူနာဖြန့်ဝေမှု၏ ခိုင်မာသော ဥပမာတစ်ခုနှင့် ထို့အပြင်၊ အသုံးအများဆုံးနမူနာဖြန့်ဝေမှုအမျိုးအစားများအတွက် ဖော်မြူလာများကို သင်တွေ့လိမ့်မည်။
နမူနာဖြန့်ဝေမှုကား အဘယ်နည်း။
နမူနာဖြန့်ဝေခြင်း သို့မဟုတ် နမူနာဖြန့်ဝေခြင်း သည် လူဦးရေတစ်ခုမှ ဖြစ်နိုင်ခြေရှိသော နမူနာအားလုံးကို ထည့်သွင်းစဉ်းစားခြင်းမှ ထွက်ပေါ်လာသော ဖြန့်ဝေမှုဖြစ်သည်။ တစ်နည်းဆိုရသော် နမူနာဖြန့်ဝေမှုသည် လူဦးရေမှဖြစ်နိုင်သောနမူနာအားလုံး၏နမူနာဘောင်ကို တွက်ချက်ခြင်းဖြင့် ရရှိသောဖြန့်ဖြူးမှုဖြစ်သည်။
ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် ကိန်းဂဏန်းလူဦးရေတစ်ခုမှ ဖြစ်နိုင်သောနမူနာအားလုံးကို ထုတ်ယူပြီး နမူနာတစ်ခုစီ၏ပျမ်းမျှအား တွက်ချက်ပါက၊ နမူနာအစုသည် နမူနာဖြန့်ဝေမှုပုံစံကို ဆိုလိုပါသည်။ ပို၍တိကျသည်မှာ၊ တွက်ချက်ထားသော parameter သည် ဂဏန်းသင်္ချာဆိုလိုဖြစ်သောကြောင့်၊ ၎င်းသည် mean ၏နမူနာခွဲဝေမှုဖြစ်သည်။
စာရင်းဇယားများတွင်၊ နမူနာတစ်ခုအား လေ့လာသောအခါ လူဦးရေကန့်သတ်ချက်၏တန်ဖိုးကို ချဉ်းကပ်နိုင်ခြေကို တွက်ချက်ရန်အတွက် နမူနာဖြန့်ဝေမှုကို အသုံးပြုသည်။ အလားတူ၊ နမူနာဖြန့်ဝေမှုသည် ပေးထားသောနမူနာအရွယ်အစားအတွက် နမူနာအမှားကို ခန့်မှန်းနိုင်စေပါသည်။
နမူနာဖြန့်ဝေခြင်း၏နမူနာ
အခုနမူနာဖြန့်ချီခြင်းရဲ့ အဓိပ္ပါယ်ကို ကျွန်ုပ်တို့သိပြီး သဘောတရားကို အပြည့်အဝနားလည်ရန် ရိုးရှင်းသောဥပမာတစ်ခုကို ကြည့်ကြပါစို့။
- ဘောက်စ်တစ်ခုတွင် ကျွန်ုပ်တို့သည် ဘောလုံးသုံးလုံးထည့်ထားပြီး တစ်ခုစီတွင် တစ်ခုမှ သုံးခုအထိ နံပါတ်တစ်ခုစီပါရှိသည်၊ ထို့ကြောင့် ဘောလုံးတစ်လုံးတွင် နံပါတ် 1 ရှိသည်၊ အခြားဘောလုံးတစ်ခုတွင် နံပါတ် 2 ရှိပြီး နောက်ဆုံးဘောလုံးသည် နံပါတ် 3 ရှိသည်။ နမူနာတစ်ခုအတွက် အရွယ်အစား n = 2၊ အစားထိုးနမူနာများကို ရွေးချယ်ပါက ပျမ်းမျှ၏နမူနာဖြန့်ဝေမှု၏ ဖြစ်နိုင်ခြေများကို တွက်ချက်သည်။
နမူနာများကို အစားထိုးခြင်းဖြင့် ရွေးချယ်ထားသည်၊ ဆိုလိုသည်မှာ နမူနာ၏ ပထမဒြပ်စင်ကို ရွေးချယ်ရန် ကောက်ယူထားသော ဘောလုံးကို အကွက်ထဲသို့ ပြန်ပို့ပေးပြီး ဒုတိယထုတ်ယူချိန်တွင် ထပ်မံရွေးချယ်နိုင်ပါသည်။ ထို့ကြောင့် လူဦးရေမှ ဖြစ်နိုင်သော နမူနာများ မှာ-
၁.၁ ၁.၂ ၁.၃
၂.၁ ၂.၂ ၂.၃
၃.၁ ၃.၂ ၃.၃
ထို့ကြောင့် ဖြစ်နိုင်သော နမူနာတစ်ခုစီ၏ ဂဏန်းသင်္ချာပျမ်းမျှကို တွက်ချက်ပါသည်။
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ထို့ကြောင့်၊ လူဦးရေမှ ကျပန်းနမူနာကို ရွေးချယ်သည့်အခါ နမူနာတန်ဖိုးတစ်ခုစီကို ရရှိရန် ဖြစ်နိုင်ခြေများမှာ အောက်ပါအတိုင်းဖြစ်သည်-
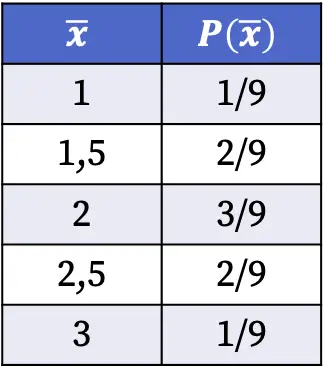
အထက်ဇယားတွင်ပြသထားသောနမူနာဖြန့်ဝေခြင်း၏ဖြစ်နိုင်ခြေများကို ဖြစ်နိုင်ခြေရှိသောကိစ္စရပ်များ၏စုစုပေါင်းအရေအတွက်ဖြင့်ဆိုလိုသောတန်ဖိုးကိုဖော်ပြထားသောနမူနာအရေအတွက်ကိုပိုင်းခြားခြင်းဖြင့်တွက်ချက်သည်။ ဥပမာ- နမူနာဆိုလိုသည် ဖြစ်နိုင်ချေ ကိုးခုအနက် နှစ်ခုတွင် 1.5 ဖြစ်သည်၊ ထို့ကြောင့် P(1.5)=2/9။
နမူနာဖြန့်ဝေမှု အမျိုးအစားများ
နမူနာဖြန့်ဝေမှုများ (သို့မဟုတ်နမူနာဖြန့်ဝေမှုများ) သည် ၎င်းတို့ရရှိထားသောနမူနာပါရာမီတာအပေါ် အခြေခံ၍ အမျိုးအစားခွဲခြားနိုင်သည်။ ထို့ကြောင့်၊ အသုံးအများဆုံး ဖြန့်ဖြူးမှုအမျိုးအစားများမှာ အောက်ပါအတိုင်းဖြစ်သည်။
- ပျမ်းမျှ၏နမူနာဖြန့်ဝေမှု – ဤသည်မှာ နမူနာတစ်ခုစီ၏ ဂဏန်းသင်္ချာပျမ်းမျှတွက်ချက်ခြင်းမှ ထွက်ပေါ်လာသော နမူနာဖြန့်ဝေမှုဖြစ်သည်။
- အချိုးအစားနမူနာဖြန့်ဝေခြင်း – ၎င်းသည်နမူနာအားလုံး၏အချိုးအစားကိုတွက်ချက်ခြင်းဖြင့်ရရှိသောနမူနာဖြန့်ဝေမှုဖြစ်သည်။
- ကွဲလွဲမှု၏နမူနာခွဲဝေမှု – ဤသည်မှာ နမူနာတွင်ကွဲလွဲမှုအားလုံး၏အစုအဝေးကို ပုံဖော်ပေးသည့်နမူနာဖြန့်ဝေမှုဖြစ်သည်။
- ကွဲပြားမှု၏ အဓိပ္ပါယ်မှာ နမူနာဖြန့်ဝေခြင်း : မတူညီသော လူဦးရေနှစ်ခုမှ ဖြစ်နိုင်ချေရှိသော နမူနာများအကြား ကွာခြားချက်ကို တွက်ချက်ခြင်းမှ ထွက်ပေါ်လာသော နမူနာဖြန့်ဝေမှုဖြစ်သည်။
- အချိုးအစားနမူနာဖြန့်ဝေမှု ကွာခြားချက် – လူဦးရေနှစ်ခုမှ ဖြစ်နိုင်သောနမူနာအချိုးအားလုံးကို နုတ်ခြင်းဖြင့် ရရှိသောနမူနာဖြန့်ဝေမှုဖြစ်သည်။
နမူနာဖြန့်ဝေမှု အမျိုးအစားတစ်ခုစီကို အောက်တွင် အသေးစိတ်ရှင်းပြထားပါသည်။
နမူနာဖြန့်ချီခြင်းကို ဆိုလိုသည်။
သာမန်ဖြစ်နိုင်ခြေဖြန့်ဝေမှုအား ပျမ်းမျှအားဖြင့် လိုက်နာသော လူဦးရေကို ပေးသည်။
![]()
နှင့် စံသွေဖည်ခြင်း။
![]()
နှင့် အရွယ်အစားနမူနာများကို ထုတ်ယူသည်။
![]()
၊ ပျမ်းမျှ၏နမူနာဖြန့်ဝေမှုကိုလည်း အောက်ပါလက္ခဏာများပါရှိသော ပုံမှန်ဖြန့်ဖြူးမှုဖြင့် သတ်မှတ်ပေးလိမ့်မည်-
![Rendered by QuickLaTeX.com \begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-44571aa7337b095ab9c9fa1f746e93a5_l3.png)
ရွှေ
![]()
ဆိုသည်မှာ ပျမ်းမျှ နှင့် ဥပမာ ဖြန့်ဝေခြင်း၏ ဆိုလိုရင်းဖြစ်သည်။
![]()
၎င်း၏စံသွေဖည်မှုဖြစ်သည်။ ထိုမျှသာမက၊
![]()
နမူနာဖြန့်ဝေမှု၏ စံအမှားဖြစ်သည်။
မှတ်ချက်- လူဦးရေသည် ပုံမှန်ဖြန့်ဝေမှုကို မလိုက်နာသော်လည်း နမူနာအရွယ်အစားသည် ကြီးမားပါက (n>30)၊ ဆိုလိုရင်း၏နမူနာဖြန့်ဝေမှုကို ဗဟိုသီအိုရီကန့်သတ်ချက်ဖြင့် အထက်တွင်ဖော်ပြထားသော ပုံမှန်ဖြန့်ဝေမှုကိုလည်း ခန့်မှန်းနိုင်သည်။
ထို့ကြောင့်၊ ဆိုလိုရင်း၏နမူနာဖြန့်ဝေမှုသည် သာမန်ဖြန့်ဖြူးမှုတစ်ခုနောက်တွင်ရှိသောကြောင့်၊ နမူနာဆိုလိုမှုနှင့်ပတ်သက်၍ ဖြစ်နိုင်ခြေတစ်စုံတစ်ရာကို တွက်ချက်ရန်အတွက် ဖော်မြူလာ မှာ-

ရွှေ-
-

နမူနာဆိုလိုသည်။
-

ဒါက လူဦးရေ ပျမ်းမျှပါ။
-

လူဦးရေစံနှုန်းသွေဖည်သည်။
-

နမူနာအရွယ်အစားဖြစ်သည်။
-

စံပုံမှန်ဖြန့်ဝေမှု N(0,1) မှသတ်မှတ်ထားသော ကိန်းရှင်တစ်ခုဖြစ်သည်။
အချိုးအစားနမူနာ ဖြန့်ဝေခြင်း။
တကယ်တော့၊ နမူနာတစ်ခုရဲ့ အချိုးအစားတစ်ခုကို လေ့လာတဲ့အခါ၊ အောင်မြင်မှုကိစ္စတွေကို ခွဲခြမ်းစိတ်ဖြာပါတယ်။ ထို့ကြောင့်၊ လေ့လာမှုရှိ ကျပန်းကိန်းရှင်သည် binomial probability ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်သည်။
ဗဟိုကန့်သတ်သီအိုရီအရ၊ ကြီးမားသောအရွယ်အစားများ (n>30) အတွက် ကျွန်ုပ်တို့သည် သာမန်ဖြန့်ဖြူးမှုတစ်ခုနှင့် ပို၍နီးကပ်စွာ binomial distribution ကို ယူဆောင်လာနိုင်သည်။ ထို့ကြောင့်၊ အချိုးအစားနမူနာဖြန့်ဝေမှုသည် အောက်ပါဘောင်များနှင့်အတူ ပုံမှန်ဖြန့်ဖြူးမှုကို ခန့်မှန်းသည်-
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f3408076893f390bb65baecfe38e6eff_l3.png)
ရွှေ
![]()
အောင်မြင်မှု၏ ဖြစ်နိုင်ခြေနှင့်
![]()
ပျက်ကွက်ခြင်း၏ ဖြစ်နိုင်ခြေဖြစ်သည်။
![]()
.
မှတ်ချက်- အကယ်၍ binomial ဖြန့်ဝေမှုသည် သာမန်ဖြန့်ဝေမှုတစ်ခုနှင့်သာ ခန့်မှန်းနိုင်သည်။

![]()
နှင့်
![]()
.
ထို့ကြောင့်၊ အချိုးအစားနမူနာဖြန့်ဝေမှုသည် ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခုသို့ ခန့်မှန်းနိုင်သောကြောင့်၊ နမူနာတစ်ခု၏ အချိုးအစားနှင့်ဆက်စပ်သော ဖြစ်နိုင်ခြေမှန်သမျှကို တွက်ချက်ရန်အတွက် ဖော်မြူလာ မှာ-

ရွှေ-
-

နမူနာအချိုးဖြစ်သည်။
-

လူဦးရေအချိုးအစားဖြစ်ပါသည်။
-

လူဦးရေ၏ ကျရှုံးမှုဖြစ်နိုင်ခြေ၊

.
-

နမူနာအရွယ်အစားဖြစ်သည်။
-

စံပုံမှန်ဖြန့်ဝေမှု N(0,1) မှသတ်မှတ်ထားသော ကိန်းရှင်တစ်ခုဖြစ်သည်။
ကွဲပြားမှု၏နမူနာဖြန့်ဝေခြင်း။
ကွဲလွဲမှု၏နမူနာဖြန့်ဝေမှုကို chi-square ဖြစ်နိုင်ခြေဖြန့်ဝေမှုဖြင့် သတ်မှတ်သည်။ ထို့ကြောင့်၊ ကွဲလွဲမှုနမူနာခွဲဝေမှု၏ ကိန်းဂဏန်းအချက်အလက်များအတွက် ဖော်မြူလာ မှာ-
![]()
ရွှေ-
-

chi-square ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်သည့် ကွဲပြားမှုနမူနာဖြန့်ဝေမှု၏ ကိန်းဂဏန်းစာရင်းအင်းဖြစ်သည်။
-

နမူနာအရွယ်အစားဖြစ်သည်။
-

နမူနာကွဲလွဲမှုဖြစ်သည်။
-

လူဦးရေကွဲလွဲမှုဖြစ်ပါသည်။
ကွဲပြားမှု၏နမူနာ ဖြန့်ချီခြင်းကို ဆိုလိုသည်။
နမူနာအရွယ်အစားသည် အလုံအလောက်ကြီးနေပါက (n 1 ≥30 နှင့် n 2 ≥30)၊ ပျမ်းမျှကွာခြားချက်၏နမူနာဖြန့်ဝေမှုသည် ပုံမှန်ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်သည်။ ပိုမိုတိကျစွာ၊ ပြောကြားထားသော ဖြန့်ဖြူးမှု၏ဘောင်များကို အောက်ပါအတိုင်း တွက်ချက်ပါသည်။
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-90c67b74b4e9326b7869d641a59725d9_l3.png)
မှတ်ချက်- လူဦးရေနှစ်မျိုးလုံးသည် ပုံမှန်ဖြန့်ဝေမှုများဖြစ်ပါက၊ ကွာခြားချက်၏နမူနာဖြန့်ဝေမှုသည် နမူနာအရွယ်အစားမခွဲခြားဘဲ ပုံမှန်ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်သည်။
ထို့ကြောင့်၊ ခြားနားချက်၏နမူနာခွဲဝေမှုကို သာမာန်ဖြန့်ဖြူးမှုဖြင့်သတ်မှတ်ထားသောကြောင့်၊ ဆိုလိုသည်မှာ ခြားနားချက်၏နမူနာဖြန့်ဝေမှု၏ ကိန်းဂဏန်းကို တွက်ချက်ရန်အတွက် ဖော်မြူလာ မှာ-

ရွှေ-
-

နမူနာ i ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
-

လူဦးရေရဲ့ ပျမ်းမျှ က i ပါ။
-

လူဦးရေ၏စံသွေဖည်မှု i။
-

နမူနာအရွယ်အစား i ဖြစ်ပါတယ်။
-

စံပုံမှန်ဖြန့်ဝေမှု N(0,1) မှသတ်မှတ်ထားသော ကိန်းရှင်တစ်ခုဖြစ်သည်။
မတူညီသောလူဦးရေမှနမူနာများတွင် မတူညီသောနမူနာအရွယ်အစားရှိနိုင်သည်ကို သတိပြုပါ။
အချိုးအစား ကွဲပြားမှုကို နမူနာယူခြင်း။
အချိုးအစားနမူနာခွဲဝေမှုတွင် ခြားနားချက်အတွက် ရွေးချယ်ထားသောနမူနာများကို binomial distributions ဖြင့် သတ်မှတ်သည်၊ အကြောင်းမှာ လက်တွေ့ကျသော ရည်ရွယ်ချက်များအတွက် အချိုးသည် လေ့လာတွေ့ရှိချက်စုစုပေါင်း၏ အချိုးတစ်ခုဖြစ်ပြီး၊
သို့သော်၊ ဗဟိုကန့်သတ်သီအိုရီကြောင့်၊ binomial ဖြန့်ဝေမှုများကို ပုံမှန်ဖြစ်နိုင်ခြေဖြန့်ဝေမှုများနှင့် အနီးစပ်ဆုံး ခန့်မှန်းနိုင်ပါသည်။ ထို့ကြောင့်၊ အချိုးအစားကွဲပြားမှု၏နမူနာခွဲဝေမှုကို အောက်ပါလက္ခဏာများဖြင့် သာမန်ဖြန့်ဖြူးမှုတစ်ခုသို့ ခန့်မှန်းနိုင်သည်-
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-a1ce359b5dd6d80f8d27b0b9a1034bed_l3.png)
မှတ်ချက်
![]()
၊
![]()
၊
![]()
၊
![]()
၊
![]()
နှင့်
![]()
.
ထို့ကြောင့်၊ အချိုးအစားခြားနားချက်၏နမူနာခွဲဝေမှုကို သာမန်ဖြန့်ဖြူးမှုတစ်ခုအဖြစ် ခန့်မှန်းနိုင်သောကြောင့်၊ အချိုးအစားကွာခြားမှုနမူနာဖြန့်ဝေခြင်း၏ ကိန်းဂဏန်းတွက်ချက်ခြင်းဖော်မြူလာ မှာ အောက်ပါအတိုင်းဖြစ်သည်။

ရွှေ-
-

နမူနာအချိုးက i။
-

လူဦးရေ အချိုးအစားက i။
-

လူဦးရေ၏ ကျရှုံးမှုဖြစ်နိုင်ချေ i၊

.
-

နမူနာအရွယ်အစား i ဖြစ်ပါတယ်။
-

စံပုံမှန်ဖြန့်ဝေမှု N(0,1) မှသတ်မှတ်ထားသော ကိန်းရှင်တစ်ခုဖြစ်သည်။