နမူနာအရွယ်အစား

အားဖြင့် Benjamin Anderson ဩဂုတ် 3, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် နမူနာအရွယ်အစားသည် အဘယ်ကြောင့်နည်းနှင့် စာရင်းဇယားများတွင် အရေးကြီးကြောင်း ရှင်းပြထားသည်။ ထို့အပြင်၊ သင့်လျော်သောနမူနာအရွယ်အစားကို တွက်ချက်နည်းနှင့် ဖြေရှင်းထားသောလေ့ကျင့်ခန်းကို သင်မည်ကဲ့သို့လုပ်ဆောင်သည်ကို သင်တွေ့နိုင်မည်ဖြစ်သည်။

နမူနာအရွယ်အစားကဘာလဲ။

နမူနာအရွယ်အစား (သို့မဟုတ် နမူနာအရွယ်အစား ) သည် လေ့လာမှုတစ်ခု၏နမူနာကို ပေါင်းစပ်ထားသည့် ပုဂ္ဂိုလ်အရေအတွက်ဖြစ်သည်။ စာရင်းဇယားများတွင် နမူနာအရွယ်အစားသည် အရေးကြီးသောကြောင့် နမူနာသည် လူဦးရေတစ်ခုလုံးကို ကိုယ်စားပြုပါသည်။

ထို့ကြောင့်၊ စာရင်းအင်းလေ့လာမှုတစ်ခု၏နမူနာအရွယ်အစားသည် လူဦးရေတစ်ခုလုံး၏ဝိသေသလက္ခဏာများကိုကိုယ်စားပြုရန်လုံလောက်သောကြီးမားရမည်ဖြစ်သည်။ အခြားတစ်ဖက်တွင်၊ နမူနာအရွယ်အစားသည် အလွန်ကြီးကြီးမားမားမဖြစ်နိုင်ပါ၊ အဘယ်ကြောင့်ဆိုသော် သုတေသနပြုမှုသည် ပိုမိုစျေးကြီးလာသောကြောင့်ဖြစ်သည်။ နိဂုံးချုပ်အားဖြင့်၊ နမူနာအရွယ်အစားသည် လုံလောက်သည်၊ ကြီးလွန်းသည်ဖြစ်စေ၊ သေးငယ်သည်ဖြစ်စေ မရှိသင့်ပါ။

ဥပမာ- နိုင်ငံတစ်ခုရဲ့ အမြင့်ကို ခွဲခြမ်းစိတ်ဖြာချင်ရင်တော့ စစ်တမ်းက အချိန်ကြာပြီး စျေးအရမ်းကြီးတဲ့အတွက် နိုင်ငံသူနိုင်ငံသားအားလုံးရဲ့ အမြင့်ကို တောင်းလို့မရပါဘူး။ ထို့ကြောင့် ကျပန်းနမူနာကောက်ယူပြီး လူဦးရေ၏ ကိုယ်စားလှယ်နမူနာကိုသာ အင်တာဗျူးလုပ်ရန် လိုအပ်ပါသည်။

➤ နမူနာပုံစံများကို ကြည့်ပါ။

သင့်လျော်သောနမူနာအရွယ်အစားကို မည်သို့သိနိုင်မည်နည်း။ နောက်အပိုင်းတွင်၊ သုတေသနလိုအပ်ချက်များအပေါ်အခြေခံ၍ သင့်လျော်သောနမူနာအရွယ်အစားကို မည်သို့ဆုံးဖြတ်ရမည်နည်း။

နမူနာအရွယ်အစားကို ဘယ်လိုတွက်မလဲ။

ပျမ်းမျှအား ခန့်မှန်းရန်အတွက်၊ လိုအပ်သောနမူနာအရွယ်အစားသည် စံသွေဖည်မှု (σ) ဖြင့် မြှောက်ထားသော Z _α/2 ၏စတုရန်းနှင့် ညီမျှသည်။ ထို့ကြောင့် နမူနာအရွယ်အစားကို တွက်ချက်ရန် ဖော်မြူလာ မှာ-

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

ရွှေ-

$n$

နမူနာအရွယ်အစားဖြစ်သည်။
$\alpha$

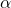
လိုချင်သော အရေးပါမှုအဆင့်ဖြစ်သည်။ ဒါကို ထည့်သွင်းစဉ်းစားပါ။

$1-\alpha$

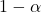
လိုချင်သောယုံကြည်မှုအဆင့်ဖြစ်သည်။
$Z_{\alpha/2}$

α/2 ၏ဖြစ်နိုင်ခြေနှင့် သက်ဆိုင်သော စံပုံမှန်ဖြန့်ဝေမှု၏ အရေအတွက်ဖြစ်သည်။ ကြီးမားသောနမူနာအရွယ်အစားများနှင့် 95% ယုံကြည်မှုအဆင့်အတွက် ၎င်းသည် များသောအားဖြင့် 1.96 နှင့် နီးစပ်ပြီး 99% ယုံကြည်မှုအဆင့်အတွက် ၎င်းသည် များသောအားဖြင့် 2.576 နှင့် နီးစပ်ပါသည်။
$\sigma$

စံသွေဖည်သည်။

ဤဖော်မြူလာတွင် လူဦးရေ ပမာဏသည် အဆုံးမရှိဟု ယူဆသည်၊ ဆိုလိုသည်မှာ လူဦးရေ အရွယ်အစားသည် အလွန်ကြီးမားသည် သို့မဟုတ် မသိရသေးကြောင်း မှတ်သားထားပါ။

မှတ်ချက်- အထက်ပါဖော်မြူလာသည် ပျမ်းမျှအတွက် ယုံကြည်မှုဖော်မြူလာကြားကာလ မှ ဆင်းသက်လာသည်။

နမူနာအရွယ်အစားတွက်ချက်မှုနမူနာ

ဤကဏ္ဍတွင်၊ ဥပမာတစ်ခုအနေဖြင့် ကိန်းဂဏန်းစစ်တမ်းတစ်ခုအတွက် သင့်လျော်သောနမူနာအရွယ်အစားကို တွက်ချက်ပါမည်။

လူဦးရေ၏စံသွေဖည်မှုသည် 15 ဝန်းကျင်ဖြစ်ကြောင်း ကျွန်ုပ်တို့သိသော်လည်း ၎င်း၏ဆိုလိုရင်းကို ကျွန်ုပ်တို့မသိသောကြောင့် ဆိုလိုရင်းကို ခန့်မှန်းရန် လေ့လာမှုတစ်ခုပြုလုပ်လိုပါသည်။ ယုံကြည်မှုအဆင့် 95% နှင့် ±2 အမှား၏အနားသတ်ကို လိုချင်ပါက မည်သည့်နမူနာအရွယ်အစားကို လိုအပ်သနည်း။

အထက်တွင်တွေ့မြင်ရသည့်အတိုင်း နမူနာအရွယ်အစားကို တွက်ချက်ရန် ဖော်မြူလာမှာ-

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

ဤကိစ္စတွင်၊ လိုချင်သောယုံကြည်မှုအဆင့်သည် 95% ဖြစ်သောကြောင့် သက်ဆိုင်ရာ Z _α/2 တန်ဖိုးသည် 1.96 ဖြစ်သည်။

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

➤ ယုံကြည်မှုအဆင့်တန်ဖိုးများပါသောဇယားကို ကြည့်ပါ။

နောက်ဆုံးတွင်၊ ကန့်သတ်ချက်များအားလုံးသည် မည်မျှတန်ဖိုးရှိသည်ကို ယခုကျွန်ုပ်တို့သိလာသောအခါ၊ ကျွန်ုပ်တို့သည် ၎င်းတို့၏တန်ဖိုးများကို ဖော်မြူလာတွင် အစားထိုးပြီး နမူနာအရွယ်အစားကို တွက်ချက်သည်-

$\begin{aligned}\displaystyle n&=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2\\[2ex] n&=\left(\frac{1,96\cdot 15}{2}\right)^2\\[2ex] n&=216,09 \approx 217 \end{array}$

အတိုချုပ်အားဖြင့်၊ လိုချင်သောလိုအပ်ချက်များနှင့် လူဦးရေကို ခန့်မှန်းရန်၊ အနည်းဆုံး နမူနာ ၂၁၇ ခု လိုအပ်ပါသည်။

နမူနာအရွယ်အစား၊ ယုံကြည်မှုအဆင့်နှင့် အမှား၏အနားသတ်

ယုံကြည်မှုအဆင့်နှင့် လိုအပ်သော အမှား၏အနားသတ်အပေါ်မူတည်၍ လိုအပ်သောနမူနာအရွယ်အစား ကွဲပြားပါမည်။ ထို့ကြောင့်၊ နမူနာအရွယ်အစား၊ ယုံကြည်မှုအဆင့်နှင့် အမှား၏အနားသတ်များသည် အောက်ပါအတိုင်း ဆက်စပ်နေပါသည်။

နမူနာအရွယ်အစားနှင့် ယုံကြည်မှုအဆင့်သည် တိုက်ရိုက်အချိုးကျပါသည်။ ဆိုလိုသည်မှာ ယုံကြည်မှုအဆင့် တိုးလာပါက နမူနာအရွယ်အစားလည်း တိုးလာမည်ဖြစ်သည်။
နမူနာအရွယ်အစားနှင့် အမှား၏အနားသတ်သည် ပြောင်းပြန်အချိုးကျသည်။ ထို့ကြောင့်၊ အမှား၏အနားသတ်များ တိုးလာပါက နမူနာအရွယ်အစား လျော့ကျသွားမည်ဖြစ်သည်။
ထို့ကြောင့်၊ နမူနာအရွယ်အစားကို တိုးမြှင့်ခြင်းသည် ယုံကြည်မှုအဆင့်ကို တိုးစေနိုင်သည် သို့မဟုတ် အမှား၏အနားသတ်ကို လျှော့ချနိုင်သည်။

အခြားနမူနာအရွယ်အစား ဖော်မြူလာများ

ခန့်မှန်းရမည့် ဘောင်ပေါ်မူတည်၍ လိုအပ်သော နမူနာအရွယ်အစားအတွက် ဖော်မြူလာ အနည်းငယ် ကွဲပြားပါသည်။ ထို့ကြောင့်၊ ဤကဏ္ဍတွင် အချို့သော အထူးကိစ္စရပ်များတွင် နမူနာအရွယ်အစားကို တွက်ချက်ရန် အသုံးဝင်နိုင်သော အခြားသော ဖော်မြူလာများကို ကျွန်ုပ်တို့ တွေ့ရပါမည်။

နမူနာအရွယ်အစား အချိုးအစား

အချိုးအစား (p) ကို ခန့်မှန်းရန် လိုအပ်သော နမူနာအရွယ်အစားကို တွက်ချက်ရန်အတွက် ဖော်မြူလာမှာ-

$n=\cfrac{N\cdot Z_{\alpha/2}^2\cdot p\cdot (1-p)}{e^2\cdot (N-1)+Z_{\alpha/2}^2\cdot p\cdot (1-p)}$

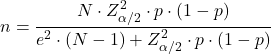
ဖြစ်နိုင်ခြေ၏နမူနာအရွယ်အစား

ဖြစ်နိုင်ခြေကို ခန့်မှန်းလိုသောအခါ၊ လိုအပ်သော နမူနာအရွယ်အစားကို ဆုံးဖြတ်ရန် အောက်ပါဖော်မြူလာကို အသုံးပြုရန် အကြံပြုလိုသည်-

$\displaystyle n=\left(\frac{Z_{\alpha/2}}{2\cdot e}\right)^2$

အမှီအခိုကင်းသော အဓိပ္ပါယ်နှစ်ခုကို နှိုင်းယှဉ်ရန်အတွက် နမူနာအရွယ်အစား

ပေးထားသော α အန္တရာယ်နှင့် β အန္တရာယ်နှင့် သီးခြားလွတ်လပ်သောနည်းလမ်းနှစ်ခုကို နှိုင်းယှဉ်သည့်အခါ နမူနာအရွယ်အစားကို တွက်ချက်ရန်အတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်-

$n=\cfrac{2\cdot \sigma^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

ရွှေ

$\Delta$

အစားထိုးယူဆချက်၏ နည်းလမ်းနှစ်ခုကြား ကွာခြားချက်ဖြစ်သည်။

တွဲထားသော နှစ်ခုကို နှိုင်းယှဉ်ခြင်းအတွက် နမူနာအရွယ်အစား

ပုံသေ အမှား α နှင့် အမှား β ဖြင့် တွဲစပ်ထားသည့် နည်းလမ်းနှစ်ခုကို နှိုင်းယှဉ်လိုပါက၊ နမူနာရှိ စူးစမ်းမှုအရေအတွက်ကို ရှာဖွေရန် အသုံးပြုရမည့် ဖော်မြူလာမှာ-

$n=\cfrac{2\cdot \sigma_d^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

ရွှေ

$\Delta$

အစားထိုးယူဆချက်နှင့် တွဲထားသောနည်းလမ်းနှစ်ခုကြား ကွာခြားချက်ဖြစ်သည်။

$\sigma_d^2$

၎င်းသည် တူညီသော လူတစ်ဦးချင်း၏ တိုင်းတာမှုနှစ်ခုကြား ကွဲလွဲမှုဖြစ်သည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။