Posterior ဖြစ်နိုင်ခြေ- အဓိပ္ပါယ် + ဥပမာ

Posteriori ဖြစ်နိုင်ခြေ ဆိုသည်မှာ အချက်အလက်အသစ်များကို ထည့်သွင်းတွက်ချက်ပြီးနောက် ဖြစ်ရပ်တစ်ခု ဖြစ်ပေါ်လာမည့် အပ်ဒိတ်ဖြစ်နိုင်ခြေဖြစ်သည်။

ဥပမာအားဖြင့်၊ မကြာသေးမီက ဖြစ်ပွားခဲ့သည့် ဖြစ်ရပ် “ B” အတွက် စာရင်းအင်းပြီးနောက် ဖြစ်ရပ် “ A” ဖြစ်ပေါ်လာမည့် ဖြစ်နိုင်ခြေကို ကျွန်ုပ်တို့ စိတ်ဝင်စားပေမည်။ အောက်ပါဖော်မြူလာကို အသုံးပြု၍ ဤနောက်ပိုင်းဖြစ်နိုင်ခြေကို ကျွန်ုပ်တို့ တွက်ချက်နိုင်သည်-

P(A|B) = P(A) * P(B|A) / P(B)

ရွှေ-

P(A|B) = ထိုဖြစ်ရပ် B ဖြစ်ပေါ်လာသောကြောင့် အဖြစ်အပျက် A ဖြစ်ပေါ်လာမည့် ဖြစ်နိုင်ခြေ။ “| » ပေးသည် ဟု ဆိုလိုသည်။

P(A) = ထိုဖြစ်ရပ် A ဖြစ်ပေါ်လာနိုင်ခြေ။

P(B) = အဆိုပါဖြစ်ရပ် B ဖြစ်ပေါ်လာနိုင်ခြေ။

P(B|A) = ထိုဖြစ်ရပ် A ဖြစ်ပေါ်လာသောကြောင့် အဆိုပါဖြစ်ရပ် B ဖြစ်ပေါ်လာမည့် ဖြစ်နိုင်ခြေ။

ဥပမာ- နောက်ဆက်တွဲဖြစ်နိုင်ခြေကို တွက်ချက်ခြင်း။

သစ်တောတစ်ခုတွင် ပိတ်ပင် 20% နှင့် မေပယ် 80% တို့ဖြင့် ဖွဲ့စည်းထားသည်။ ဝက်သစ်ချပင်တွေရဲ့ 90% က ကျန်းမာပြီး မေပယ်ရဲ့ 50% ကသာ ကျန်းမာတယ်ဆိုပါစို့။ အကွာအဝေးကနေ သစ်ပင်တစ်ပင် ကျန်းမာတယ်လို့ ပြောနိုင်တယ်ဆိုပါစို့။ သစ်ပင်သည် သပိတ်ပင်ဖြစ်နိုင်ခြေ မည်မျှရှိသနည်း။

အဖြစ်အပျက် B ဖြစ်ခဲ့သည့်အတွက် ဖြစ်ရပ် A ဖြစ်ပေါ်လာမည့် ဖြစ်နိုင်ခြေကို သတိရပါ-

P(A|B) = P(A) * P(B|A) / P(B)

ဤဥပမာတွင်၊ သစ်ပင်သည် ကျန်းမာသည်ဟု ပေးသော ပိတ်ပင်မှုဖြစ်နိုင်ခြေမှာ-

P(Oak|Healthy) = P(Oak) * P(Healthy|Oak) / P(ကျန်းမာသော)

P(Oak) = ပေးထားသောသစ်ပင်သည် ဝက်သစ်ချသားဖြစ်နိုင်ခြေမှာ 0.2 ဖြစ်သောကြောင့် သစ်တောရှိ သစ်ပင်အားလုံး၏ 20% သည် ပိတ်ပင်ထားသည်။

P(Healthy) = ပေးထားသော သစ်ပင်တစ်ပင်သည် ကျန်းမာသော ဖြစ်နိုင်ခြေကို အောက်ပါအတိုင်း တွက်ချက်နိုင်သည်- (0.20)*(0.9) + (0.8)*(0.5) = 0.58 ။

P(Healthy|Oak) = ဝက်သစ်ချပင်ဖြစ်နိုင်ခြေသည် 0.9 ဖြစ်ပြီး၊ ပိတ်ပင်ထားသော 90% သည် ကျန်းမာသည်ဟု ကျွန်ုပ်တို့ပြောလာသောကြောင့်ဖြစ်သည်။

ဤဂဏန်းသုံးလုံးကို အသုံးပြု၍ အပင်သည် ကျန်းမာသည်ဟု ပေးထားသည့် ဝက်သစ်ချပင်ဖြစ်နိုင်ခြေကို ကျွန်ုပ်တို့ ရှာဖွေနိုင်သည်-

P(Oak|Healthy) = P(Oak) * P(Healthy|Oak) / P(Healthy) = (0.2) * (0.9) / (0.58) = 0.3103 ။

ဤဖြစ်နိုင်ခြေကို အလိုလိုနားလည်နိုင်ရန် အောက်ပါဇယားကွက်သည် သစ်ပင် 100 ၏ သစ်တောကို ကိုယ်စားပြုသည်ဟု ယူဆကြပါစို့။ အပင် 20 တိတိသည် ပိတ်ပင်ထားပြီး 18 ပင်သည် ကျန်းမာသည်။ အခြားသစ်ပင် ၈၀ မှာ မေပယ်ပင်ဖြစ်ပြီး ၄၀ မှာ ကျန်းမာသန်စွမ်းသည်။

(အို = Oak၊ M = Maple၊ အစိမ်းရောင် = ကျန်းမာ၊ အနီရောင် = မကျန်းမာ)

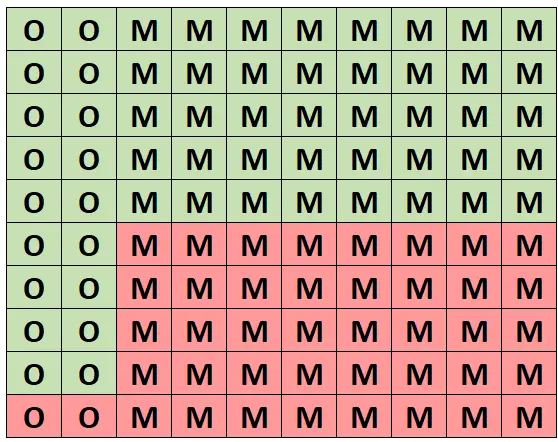
အပင်အားလုံးတွင် ၅၈ ပင် အတိအကျ ကျန်းမာပြီး ထိုကျန်းမာသော သစ်ပင် ၁၈ ပင်သည် ပိတ်ပင်ထားသည်။ ထို့ကြောင့် ကျွန်ုပ်တို့သည် ကျန်းမာသောအပင်ကို ရွေးထားကြောင်း သိပါက ၎င်းသည် ဝက်သစ်ချပင်ဖြစ်နိုင်ခြေမှာ 18/58 = 0.3103 ဖြစ်သည်။

နောက်ပိုင်း ဖြစ်နိုင်ခြေကို ဘယ်အချိန်မှာ သုံးသင့်သလဲ။

နောက်ဆက်တွဲဖြစ်နိုင်ခြေကို ဘဏ္ဍာရေး၊ ဆေးပညာ၊ စီးပွားရေးနှင့် မိုးလေဝသခန့်မှန်းချက်အပါအဝင် နယ်ပယ်များစွာတွင် အသုံးပြုသည်။

နောက်ပိုင်းဖြစ်နိုင်ချေများကို အသုံးပြုခြင်း၏အချက်မှာ သတင်းအချက်အလက်အသစ်များရရှိပြီးသည်နှင့် တစ်စုံတစ်ခုနှင့်ပတ်သက်၍ ကျွန်ုပ်တို့တွင်ရှိခဲ့သော ကြိုတင်ယုံကြည်ချက်တစ်ခုကို အပ်ဒိတ်လုပ်ရန်ဖြစ်သည်။

သစ်တောတွင် ပေးထားသောသစ်ပင်သည် ဝက်သစ်ချပင်ဖြစ်နိုင်ခြေ 20% ရှိကြောင်း ယခင်ဥပမာမှ ပြန်ပြောင်းသတိရပါ။ ၎င်းကို ကြိုတင်ဖြစ်နိုင်ခြေ ဟု ခေါ်သည်။ အကယ်၍ ကျွန်ုပ်တို့သည် သစ်ပင်တစ်ပင်ကို ကျပန်းရွေးချယ်ခဲ့မည်ဆိုလျှင်၊ ဝက်သစ်ချပင်ဖြစ်နိုင်ခြေမှာ 0.20 ဖြစ်သည်ကို ကျွန်ုပ်တို့သိပါသည်။

သို့သော်၊ ကျွန်ုပ်တို့ရွေးချယ်ထားသောသစ်ပင်သည် ကျန်းမာသန်စွမ်းကြောင်း သတင်းအချက်အလက်အသစ်ကိုရရှိသည်နှင့်တစ်ပြိုင်နက် ဤသစ်ပင်၏နောက်ဆက်တွဲ ဖြစ်နိုင်ခြေမှာ 0.3103 အစား 0.3103 ဖြစ်သည်ကို ဆုံးဖြတ်ရန် ကျွန်ုပ်တို့အသုံးပြုနိုင်ပါသည်။

လက်တွေ့ကမ္ဘာမှာ လူတွေဟာ သတင်းအချက်အလက်အသစ်တွေကို အဆက်မပြတ်ရှာဖွေနေပါတယ်။ ဤအချက်အလက်အသစ်က ကျွန်ုပ်တို့၏ယခင်ယုံကြည်ချက်များကို အပ်ဒိတ်လုပ်ရန် ကူညီပေးသည်။ ကိန်းဂဏန်းအသုံးအနှုန်းများတွင်၊ ဆိုလိုသည်မှာ ကျွန်ုပ်တို့သည် ကမ္ဘာကြီးကို ပိုမိုတိကျသောနားလည်မှုရရှိစေရန်နှင့် အနာဂတ်ဖြစ်ရပ်များနှင့်ပတ်သက်၍ ပိုမိုတိကျသောခန့်မှန်းချက်များကို ပြုလုပ်နိုင်စေသည့် ဖြစ်ပေါ်လာသည့်နောက်ဆက်တွဲဖြစ်နိုင်ချေများကို ကျွန်ုပ်တို့ဖန်တီးနိုင်သည်ဟု ဆိုလိုသည်။