စံပုံမှန် ဖြန့်ဖြူးမှု

အားဖြင့် Benjamin Anderson ဩဂုတ် 4, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် စံပုံမှန်ဖြန့်ဝေမှုမှာ အဘယ်အရာနှင့် ၎င်းကိုအသုံးပြုကြောင်း ရှင်းပြထားသည်။ စံပုံမှန်ဖြန့်ဖြူးမှု၏ဂုဏ်သတ္တိများ၊ ၎င်း၏ဝိသေသတန်ဖိုးများနှင့်အတူဇယားနှင့်အပြင်၊ ဖြေရှင်းနိုင်သောလေ့ကျင့်ခန်းတစ်ခုကိုလည်းသင်တွေ့လိမ့်မည်။

စံပုံမှန်ဖြန့်ဝေမှုဆိုသည်မှာ အဘယ်နည်း။

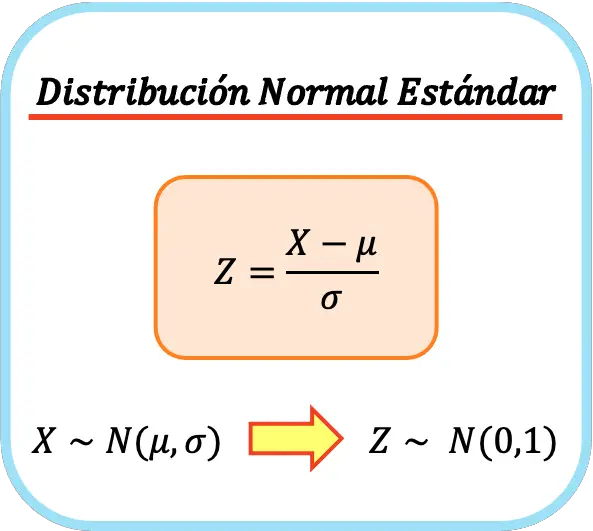
စံပုံမှန်ဖြန့်ဖြူးမှု ယူနစ်ပုံမှန်ဖြန့်ဝေမှု ဟုလည်း ခေါ်သည်၊ ပုံမှန်ဖြန့်ဝေမှု၏ အရိုးရှင်းဆုံးကိစ္စဖြစ်သည်။ ပို၍တိကျသည်မှာ၊ စံပုံမှန်ဖြန့်ဖြူးမှုသည် ပျမ်းမျှနှင့်စံသွေဖည်တန်ဖိုးများ 0 နှင့် 1 အသီးသီးရှိသော ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။

ထို့ကြောင့်၊ စံပုံမှန်ဖြန့်ဝေမှုကို N(0,1) ဟုသတ်မှတ်ထားပြီး ပထမဘောင်သည် ဖြန့်ဖြူးမှု၏ပျမ်းမျှဖြစ်ပြီး ဒုတိယဘောင်သည် ၎င်း၏စံသွေဖည်မှု (သို့မဟုတ် SD) ဖြစ်သည်။

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

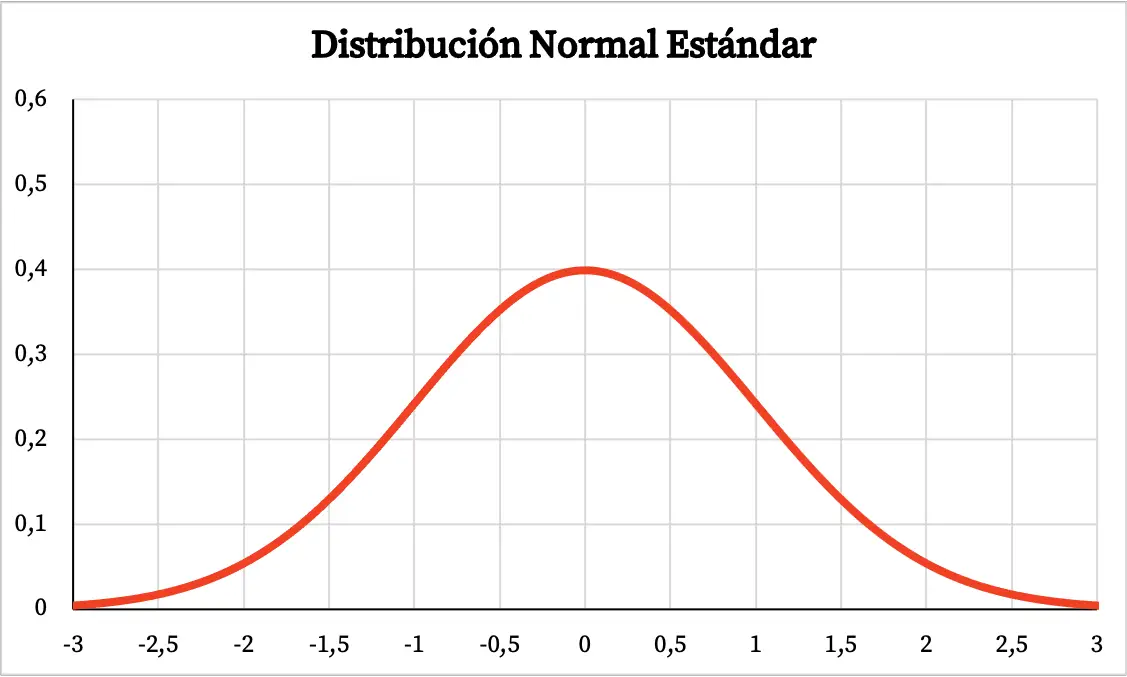
ထို့ကြောင့် စံပုံမှန်ဖြန့်ဝေမှု၏ဂရပ်သည် အောက်ပါအတိုင်းဖြစ်သည်။

စံပုံမှန်ဖြန့်ဖြူးမှုအတွက် ဖော်မြူလာ

ပုံမှန်ဖြန့်ဖြူးမှုမှန်သမျှကို စံပုံမှန်ဖြန့်ဝေမှုအဖြစ်သို့ ပြောင်းလဲရန်၊ ပုံမှန်ဖြန့်ဖြူးမှု၏ပျမ်းမျှအား ၎င်း၏တန်ဖိုးများအားလုံးမှ နုတ်ပြီး ပုံမှန်ဖြန့်ဝေမှု၏ စံသွေဖည်မှုဖြင့် ပိုင်းခြားရမည်ဖြစ်သည်။

ထို့ကြောင့် စံပုံမှန်ဖြန့်ဝေမှုအတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်။

ဤနည်းအားဖြင့်၊ ကိန်းရှင်အသစ်၏ ဂဏန်းသင်္ချာပျမ်းမျှနှင့် စံသွေဖည်မှုသည် 0 နှင့် 1 အသီးသီးဖြစ်လိမ့်မည်၊ ထို့ကြောင့် ကျွန်ုပ်တို့သည် စံပုံမှန်ဖြန့်ဖြူးမှုကို ရရှိမည်ဖြစ်သည်။ ဤလုပ်ငန်းစဉ်ကို univariate normalization သို့မဟုတ် univariate normalization ဟုခေါ်သည်။

စံပုံမှန် ဖြန့်ဖြူးရေးဇယား

စံပုံမှန် ဖြန့်ဝေမှု၏ ဇယားသည် စံပုံမှန် ဖြန့်ဝေမှု၏ ပေးထားသော တန်ဖိုးထက် မှတ်သားထားသော တန်ဖိုးထက် လျော့နည်းသည့် ဖြစ်နိုင်ခြေများပါရှိသော ဇယားတစ်ခု ဖြစ်သည်။

ထို့အပြင်၊ ပုံမှန်ဖြန့်ဖြူးမှု၏လုပ်ဆောင်ချက်သည် ၎င်း၏ပျမ်းမျှနှင့်စံသွေဖည်မှုပေါ်တွင်မူတည်သောကြောင့်၊ ပုံမှန်ဖြန့်ဖြူးမှု၏ဖြစ်နိုင်ခြေကိုဆုံးဖြတ်ရန် စံပုံမှန်ဖြန့်ဝေမှုဇယားကို တိုးချဲ့ခြင်းဖြင့်လည်း အသုံးပြုပါသည်။ ထိုသို့လုပ်ဆောင်ရန်၊ ပုံမှန်ဖြန့်ဖြူးမှုကို စံပုံမှန်ဖြန့်ဝေမှုတစ်ခုအဖြစ် ရိုက်ထည့်ပြီးနောက် ၎င်းနှင့် သက်ဆိုင်သည့် ဖြစ်နိုင်ခြေကို ဇယားတွင် ကြည့်ရှုပါ။

ထို့ကြောင့်၊ စံပုံမှန် ဖြန့်ဖြူးရေးဇယားရှိ တန်ဖိုးများသည် အောက်ပါအတိုင်းဖြစ်သည်။

Standard Normal Distribution ၏ ဥပမာ

ယခု ကျွန်ုပ်တို့သည် စံပုံမှန်ဖြန့်ဖြူးခြင်း၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ၎င်း၏ဖော်မြူလာဟူသည် အဘယ်အရာဖြစ်သည်ကို သိရှိပြီး အောက်တွင် သဘောတရားကို ကောင်းစွာနားလည်ရန် ခိုင်မာသော ဥပမာတစ်ခုဖြစ်သည်။

စဉ်ဆက်မပြတ် ကျပန်းပြောင်းလဲနိုင်သောကိန်းရှင်သည် ပျမ်းမျှ 45 နှင့် စံသွေဖည်မှု 15 ဖြင့် ပုံမှန်ဖြန့်ဖြူးမှုနောက်တွင် လိုက်နေသည်၊ 58 ထက်နည်းသော သို့မဟုတ် ညီမျှသည့်တန်ဖိုးကိုရရှိရန် ဖြစ်နိုင်ခြေအဘယ်နည်း။

$N(45,15)\ \color{orange}\bm{\longrightarrow}\color{black}\ P[X\leq 58]= \ \color{orange}\bm{?}\color{black}$

ပုံမှန်ဖြန့်ဖြူးမှု၏ဖြစ်နိုင်ခြေကိုရှာဖွေရန်၊ ကျွန်ုပ်တို့သည် ၎င်း၏အင်္ဂါရပ်ဇယားကိုအသုံးပြုရန် လိုအပ်သော်လည်း ထိုသို့ပြုလုပ်ရန်၊ စံပုံမှန်ဖြန့်ဝေမှုရရှိရန် စာရိုက်ခြင်းလုပ်ငန်းစဉ်ကို ဦးစွာလုပ်ဆောင်ရန် လိုအပ်သည်။ ထို့ကြောင့် ကျွန်ုပ်တို့သည် စံပုံမှန် ဖြန့်ဖြူးရေးဖော်မြူလာကို အသုံးပြုသည်-

$Z=\cfrac{X-\mu}{\sigma}$

ဒါကြောင့် ဖြစ်နိုင်ခြေတန်ဖိုးကနေ ပျမ်းမျှကို နုတ်ပြီး စံသွေဖည်မှုဖြင့် ပိုင်းခြားပါ။

$\displaystyle P[X\leq 58]=P\left[Z\leq\frac{58-45}{15}\right]=P[Z\leq 0,87]$

ကျွန်ုပ်တို့သည် ကိန်းရှင်ကို စံသတ်မှတ်ပြီးသည်နှင့်၊ ကျွန်ုပ်တို့သည် 0.87 ၏တန်ဖိုးနှင့် ကိုက်ညီမှုရှိမရှိကို ကြည့်ရှုရန် စံပုံမှန် ဖြန့်ဖြူးမှုဖြစ်နိုင်ခြေဇယား (အထက်တွင်ကြည့်ပါ) သို့သွားပါ။

$\displaystyle P[Z\leq 0,87]=0,8078$

ထို့ကြောင့် 58 နှင့် ညီမျှသော သို့မဟုတ် ထက်နည်းသော တန်ဖိုးတစ်ခုရရှိရန် ဖြစ်နိုင်ခြေသည် 80.78% ဖြစ်သည်။

စံပုံမှန်ဖြန့်ဖြူးခြင်း၏ဝိသေသလက္ခဏာများ

စံပုံမှန်ဖြန့်ဝေမှုတွင် အောက်ပါလက္ခဏာများ ရှိသည်။

စံပုံမှန် ဖြန့်ဖြူးမှုသည် 0 ကို ဗဟိုပြုသည့် အချိုးညီသော ဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။
သာမာန်ဖြန့်ဖြူးမှုကဲ့သို့ပင်၊ ပုံမှန်ပုံမှန်ဖြန့်ဝေသည့်ဂရပ်သည် ခေါင်းလောင်းပုံသဏ္ဌာန်ဖြစ်ပြီး ဂရပ်ဧရိယာအများစုသည် ပျမ်းမျှပတ်လည်တွင် ကျသွားသည်။
ထို့ကြောင့်၊ ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခု၏ ပျမ်းမျှ၊ မုဒ်နှင့် အလယ်အလတ်သည် 0ဖြစ်သည့် တူညီသောတန်ဖိုးရှိသည်။
စံပုံမှန်ဖြန့်ဝေမှုတွင် အများဆုံး z=0 ရှိသည်။
အလားတူ၊ စံပုံမှန်ဖြန့်ဝေမှုတွင် z=-1 နှင့် z=+1 တွင် ဖြတ်ကူးမှုအမှတ်နှစ်ခုရှိသည်။
လက်မ၏စည်းမျဉ်းအရ၊ တန်ဖိုးများ၏ 68% သည် +1 နှင့် -1 ကြားတွင် စံပုံမှန်ဖြန့်ဖြူးမှုတွင် ကျရောက်ကြောင်း ကျွန်ုပ်တို့သိရပြီး၊ +2 နှင့် -2 ကြားရှိ တန်ဖိုးများ၏ 95% နှင့် 99.7% အကြားတန်ဖိုးများ + 3 နှင့် – 3 ။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။