ပုံမှန် ဖြန့်ဖြူးမှု

ပုံမှန်ဖြန့်ဖြူးမှုသည် စာရင်းဇယားများတွင် အသုံးအများဆုံးဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှုဖြစ်သည်။

ပုံမှန်ဖြန့်ဝေမှုများတွင် အောက်ပါလက္ခဏာများရှိသည်။

• ခေါင်းလောင်းပုံသဏ္ဍာန်
• အချိုးကျသည်။
• ပျမ်းမျှနှင့် အလယ်အလတ်သည် ညီမျှသည်။ နှစ်ခုလုံးသည် ဖြန့်ဖြူးမှု၏ဗဟိုတွင် တည်ရှိသည်။
• ဒေတာ၏ 68% ခန့်သည် စံသွေဖည်မှုတစ်ခုအတွင်း ကျရောက်နေသည်။
• ဒေတာများ၏ 95% ခန့်သည် စံသွေဖည်မှုနှစ်ခုအတွင်း ကျရောက်နေသည်။
• ဒေတာများ၏ 99.7% ခန့်သည် စံသွေဖည်မှု သုံးခုအတွင်း ကျရောက်နေသည်။

နောက်ဆုံးသုံးမှတ်ကို လက်မစည်းမျဉ်း ဟု ခေါ်သည်၊ တစ်ခါတစ်ရံ 68-95-99.7 စည်းမျဉ်း ဟု ခေါ်သည်။

ဆက်စပ်- လက်မနည်းဥပဒေ (အလေ့အကျင့်ပြဿနာများ)

ပုံမှန်မျဉ်းကွေးဆွဲနည်း

သာမာန်မျဉ်းကွေးတစ်ခုဆွဲရန် ပျမ်းမျှနှင့် စံသွေဖည်မှုကို သိရန်လိုသည်။

ဥပမာ 1- အချို့ကျောင်းရှိ အမျိုးသားများ၏ အရပ်အမြင့်ကို ပုံမှန်အားဖြင့် $\mu =\; 70\; လက်မနှင့်$ စံသွေဖည်မှု $\sigma \; =\; 2\; လက်မဖြင့်\; ဖြန့်ဝေသည်ဆိုပါစို့။\; ပုံမှန်မျဉ်းကွေးကို\; ပုံကြမ်းဆွဲပါ။$

အဆင့် 1- ပုံမှန်မျဉ်းကွေးကို ပုံကြမ်းဆွဲပါ။

အဆင့် 2- ပျမ်းမျှလက်မ 70 သည် အလယ်တွင်ရှိသည်။

အဆင့် 3- စံသွေဖည်မှုတစ်ခုစီသည် 2 လက်မအကွာအဝေးနှင့် သက်ဆိုင်သည်။

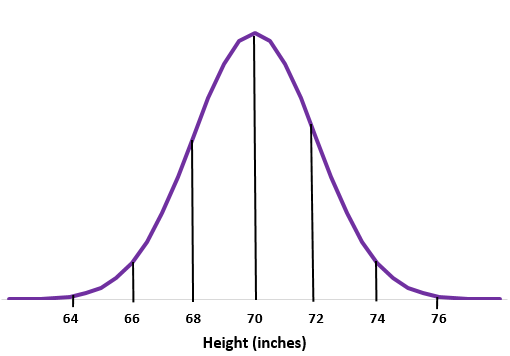
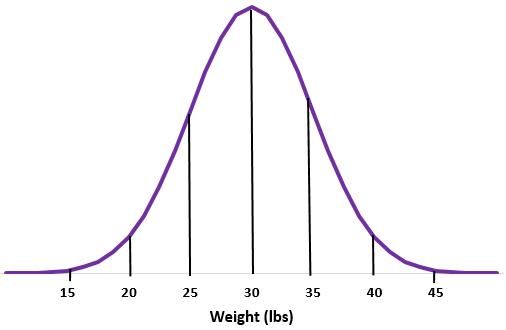
ဥပမာ 2- အချို့ဖျံမျိုးစိတ်များ၏ အလေးချိန်ကို ပုံမှန်အားဖြင့် $\mu =\; 30\; lb\; နှင့်$ စံသွေဖည်မှု $\sigma \; =\; 5\; lb$ ဖြင့် ဖြန့်ဝေသည်ဆိုပါစို့။ $ပုံမှန်မျဉ်းကွေးကို\; ပုံကြမ်းဆွဲပါ။$

အဆင့် 1- ပုံမှန်မျဉ်းကွေးကို ပုံကြမ်းဆွဲပါ။

အဆင့် 2- ပေါင် 30 ပျမ်းမျှသည် အလယ်တွင် ကျရောက်သည်။

အဆင့် 3- စံသွေဖည်မှုတစ်ခုစီသည် 5 ပေါင်အကွာအဝေးနှင့် သက်ဆိုင်သည်။

ပုံမှန်ဖြန့်ဝေမှုကို အသုံးပြု၍ ရာခိုင်နှုန်းများရှာဖွေနည်း

လက်မ၏စည်းမျဉ်း ၊ တစ်ခါတစ်ရံတွင် 68-95-99.7 ဟုခေါ်သော စည်းမျဉ်းသည် ပုံမှန်ဖြန့်ဝေထားသော ကျပန်းပြောင်းလဲမှုတစ်ခုအတွက် ဒေတာများ၏ 68% သည် စံသွေဖည်မှုတစ်ခု၏အတိုင်းအတာတစ်ခုအတွင်းတွင် ကျရောက်နေပြီး 95% သည် စံနှစ်ခု၏အကွာအဝေးအတွင်းတွင် ရှိနေသည်ဟု ဖော်ပြထားသည်။ ပျမ်းမျှမှ သွေဖည်ပြီး 99.7% သည် ပျမ်းမျှမှ စံသွေဖည်မှု သုံးခုအတွင်း ရှိပါသည်။

ဤစည်းမျဉ်းကိုအသုံးပြုခြင်းဖြင့် ရာခိုင်နှုန်းများနှင့်ပတ်သက်သောမေးခွန်းများကို ကျွန်ုပ်တို့ဖြေဆိုနိုင်ပါသည်။

ဥပမာ- အချို့သောကျောင်းရှိ အမျိုးသားများ၏ အရပ်အမြင့်ကို ပုံမှန်အားဖြင့် $\mu =\; 70\; လက်မနှင့်$ စံသွေဖည်မှု $\sigma \; =\; 2\; လက်မဖြင့်\; ဖြန့်ဝေသည်ဆိုပါစို့။$

$ဒီကျောင်းမှာ\; အရပ်\; ၇၄\; လက်မကျော်တဲ့\; အမျိုးသားတွေက\; ခန့်မှန်းခြေ\; ဘယ်လောက်ရှိလဲ။$

ဖြေရှင်းချက်-

အဆင့် 1- ပျမ်းမျှ $\mu =\; 70\; လက်မ\; နှင့်$ စံသွေဖည်မှု $\sigma \; =\; 2\; လက်မ\; ဖြင့်\; ပုံမှန်\; ဖြန့်ဖြူးမှုကို\; ပုံကြမ်းလုပ်ပါ။$

အဆင့် 2- အမြင့် 74 လက်မသည် ပျမ်းမျှအထက် စံသွေဖည်နှစ်ခုဖြစ်သည်။ ဤအမှတ်အထက် ရာခိုင်နှုန်းများကို ပုံမှန်ဖြန့်ဖြူးမှုထဲသို့ ထည့်ပါ။

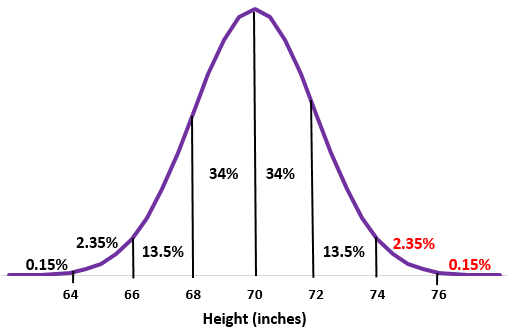
2.35% + 0.15% = 2.5%

ဤကျောင်းရှိ အမျိုးသားများ၏ 2.5% ခန့်သည် အရပ် 74 လက်မကျော်ရှိသည်။

$ဤကျောင်းရှိ\; အမျိုးသားများသည်\; ခန့်မှန်းခြေအားဖြင့်\; အရပ်\; 68\; လက်မနှင့်\; 72\; လက်မအကြားရှိကြသနည်း။$

ဖြေရှင်းချက်-

အဆင့် 1- ပျမ်းမျှ $\mu =\; 70\; လက်မ\; နှင့်$ စံသွေဖည်မှု $\sigma \; =\; 2\; လက်မ\; ဖြင့်\; ပုံမှန်\; ဖြန့်ဖြူးမှုကို\; ပုံကြမ်းလုပ်ပါ။$

အဆင့် 2- အမြင့် 68 လက်မနှင့် 72 လက်မသည် ပျမ်းမျှအောက်နှင့်အထက် စံသွေဖည်မှုတစ်ခု အသီးသီးဖြစ်သည်။ ပုံမှန်ဖြန့်ဖြူးမှုတွင် ဤအမှတ်နှစ်ခုကြားရှိ ရာခိုင်နှုန်းများကို ပေါင်းထည့်ပါ။

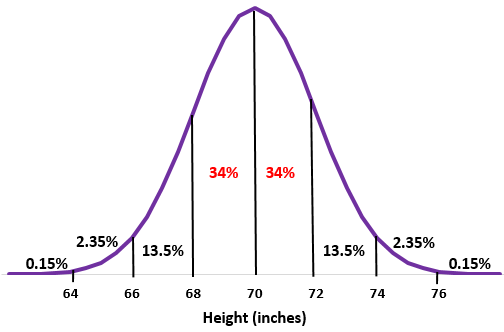
၃၄% + ၃၄% = ၆၈%၊

ဤကျောင်းရှိ အမျိုးသားများ၏ 68% ခန့်သည် အရပ် 68 လက်မနှင့် 72 လက်မကြားရှိကြသည်။

သာမာန်ဖြန့်ဖြူးမှုကို အသုံးပြု၍ အရေအတွက်များကို ရှာဖွေနည်း

အရေအတွက်ဆိုင်ရာ မေးခွန်းများကို ဖြေရန် လက်မ၏ စည်းမျဉ်းကိုလည်း အသုံးပြုနိုင်သည်။

ဥပမာ- ဖျံမျိုးစိတ်တစ်ခု၏အလေးချိန်ကို ပုံမှန်အားဖြင့် $\mu =\; 30\; ပေါင်\; နှင့်$ စံသွေဖည်မှု $\sigma \; =\; 5\; lb$ ဖြင့် ဖြန့်ဝေသည်ဆိုပါစို့။

အချို့သော နယ်မြေတွင် ဤဖျံအကောင် ၂၀၀ ရှိသည်။ ခန့်မှန်းခြေအားဖြင့် အဆိုပါဖျံများ မည်မျှအလေးချိန် ၃၅ ပေါင်ကျော်ရှိသည်။

ဖြေရှင်းချက်-

အဆင့် 1- ပျမ်းမျှ $\mu =\; 30\; ပေါင်\; နှင့်$ $\sigma \; =\; 5\; lb$ ၏ စံသွေဖည်မှုဖြင့် ပုံမှန် ဖြန့်ဖြူးမှုကို ပုံကြမ်းလုပ်ပါ။

အဆင့် 2- 35 ပေါင်အလေးချိန်သည် ပျမ်းမျှအထက် စံသွေဖည်မှုတစ်ခုဖြစ်သည်။ ဤအမှတ်အထက် ရာခိုင်နှုန်းများကို ပုံမှန်ဖြန့်ဖြူးမှုထဲသို့ ထည့်ပါ။

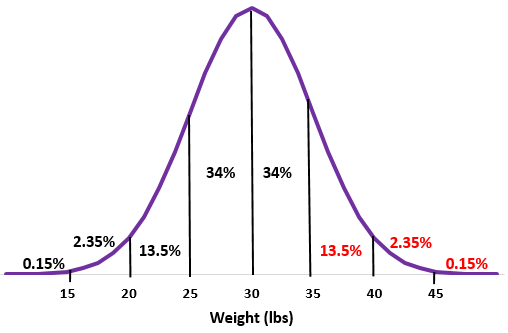
13.5% + 2.35% + 0.15% = 16%

အဆင့် 3- ကိုလိုနီတွင် ဖျံအကောင် 200 ရှိသောကြောင့် 200 = 0.16 * 200 = 32 ၏ 16%

ဤနယ်မြေရှိ ဖျံ ၃၂ ကောင်ခန့်သည် အလေးချိန် ၃၅ ပေါင်ကျော်ရှိသည်။

ခန့်မှန်းခြေအားဖြင့် ဤဒေသရှိ ဖျံကောင်ရေ မည်မျှအလေးချိန် ပေါင် 30 အောက် ရှိမည်နည်း။

အထက်တွင်ပြုလုပ်ခဲ့သည့် အဆင့်များအားလုံးကို လိုက်နာမည့်အစား၊ ပုံမှန်ဖြန့်ဝေမှု၏ ပျမ်းမျှသည် ဤကိစ္စတွင် ပေါင် 30 ဖြစ်သည့် ပျမ်းမျှနှင့် ညီမျှကြောင်း အသိအမှတ်ပြုနိုင်ပါသည်။

ဆိုလိုသည်မှာ ဖျံများ၏တစ်ဝက်သည် ကိုယ်အလေးချိန် ပေါင် 30 ကျော်ရှိပြီး ကျန်တစ်ဝက်မှာ ပေါင် 30 အောက် အလေးချိန်ရှိသည်။ ဆိုလိုသည်မှာ ဖျံ 200 ၏ 50% သည် 30 ပေါင်ထက်နည်းသောကြောင့် 0.5 * 200 = 100 ဖျံများ ဖြစ်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် ပုံမှန်ဖြန့်ဖြူးခြင်းဆိုင်ရာ နောက်ထပ်အချက်အလက်များကို ပေးဆောင်သည်-

ပုံမှန်ဖြန့်ဖြူးခြင်း၏ ခိုင်မာသော ဥပမာ ၆
ပုံမှန်ဖြန့်ဖြူးမှုနှင့် t ဖြန့်ဖြူးမှု- ကွာခြားချက်
Excel တွင် Bell Curve ဖန်တီးနည်း
Python တွင် Bell Curve ဖန်တီးနည်း