ပျမ်းမျှ၊ အလယ်အလတ်နှင့် မုဒ်

အားဖြင့် Benjamin Anderson ဩဂုတ် 5, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် အဓိပ္ပါယ်၊ အလယ်အလတ်နှင့် မုဒ်တို့ကို ရှင်းပြထားသည်။ ပျမ်းမျှ၊ အလယ်အလတ်နှင့် မုဒ်၊ ၎င်းတို့အတွက် အသုံးပြုထားပုံနှင့် ဤကိန်းဂဏန်းဆိုင်ရာ တိုင်းတာမှုသုံးခုအကြား ကွာခြားချက်မှာ အဘယ်နည်း။ ထို့အပြင်၊ အဆုံးတွင် အွန်လိုင်းဂဏန်းတွက်စက်ဖြင့် မည်သည့် ကိန်းဂဏန်းနမူနာများ၏ ပျမ်းမျှ၊ ပျမ်းမျှနှင့် မုဒ်တို့ကို တွက်ချက်နိုင်မည်ဖြစ်သည်။

ဆိုလိုရင်း၊ အလယ်အလတ်နှင့် မုဒ်ဟူသည် အဘယ်နည်း။

ပျမ်းမျှ၊ အလယ်အလတ်နှင့် မုဒ်တို့သည် ဗဟိုအနေအထား၏ ကိန်းဂဏန်းဆိုင်ရာ တိုင်းတာမှုများဖြစ်သည်။ တစ်နည်းအားဖြင့်ဆိုရသော် ပျမ်းမျှ၊ အလယ်အလတ်နှင့် မုဒ်တို့သည် ကိန်းဂဏန်းနမူနာတစ်ခုကို သတ်မှတ်ရာတွင် အထောက်အကူဖြစ်စေသော တန်ဖိုးများဖြစ်ပြီး အထူးသဖြင့် ၎င်းတို့သည် ၎င်း၏ဗဟိုတန်ဖိုးများကို ညွှန်ပြသည်။

ပျမ်းမျှ၊ အလယ်အလတ်နှင့် မုဒ်ကို အောက်ပါအတိုင်း သတ်မှတ်ထားသည်-

Mean : နမူနာရှိဒေတာအားလုံး၏ပျမ်းမျှဖြစ်သည်။
အလယ်အလတ် – ဤသည်မှာ အငယ်ဆုံးမှ အကြီးဆုံးသို့ စီထားသော ဒေတာအားလုံး၏ အလယ်တန်ဖိုးဖြစ်သည်။
မုဒ် – ဤသည်မှာ ဒေတာအတွဲတွင် အထပ်ထပ်ဆုံးတန်ဖိုးဖြစ်သည်။

ဤစာရင်းအင်းဆိုင်ရာ အစီအမံသုံးခုကို အောက်တွင် အသေးစိတ်ရှင်းပြထားပါသည်။

တစ်ဝက်

ပျမ်းမျှတွက်ချက်ရန်၊ တန်ဖိုးများအားလုံးကို ပေါင်းထည့်ပြီးနောက် ဒေတာစုစုပေါင်းအရေအတွက်ဖြင့် ပိုင်းပါ။ ထို့ကြောင့် ပျမ်းမျှအတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်။

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^N x_i}{N}$

👉 မည်သည့်ဒေတာအစုံ၏ပျမ်းမျှ၊ အလယ်အလတ်နှင့် မုဒ်တို့ကို တွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ကို သင်အသုံးပြုနိုင်ပါသည်။

ပျမ်းမျှသင်္ကေတသည် အက္ခရာ x ၏အထက်တွင် အလျားလိုက်အဝိုင်းတစ်ခုဖြစ်သည်။

$(\overline{x}).$

နမူနာဆိုလိုအား ပျမ်းမျှသင်္ကေတဖြင့် လူဦးရေဆိုလိုမှ ခွဲခြားနိုင်သည်- နမူနာတစ်ခု၏ဆိုလိုအား သင်္ကေတဖြင့် ဖော်ပြသည်

$\overline{x}$

ပျမ်းမျှအားဖြင့် လူဦးရေသည် ဂရိအက္ခရာကို အသုံးပြုသည်။

$\mu.$

ပျမ်းမျှကို ဂဏန်းသင်္ချာ ပျမ်းမျှ သို့မဟုတ် ပျမ်းမျှ ဟုလည်း ခေါ်သည်။ ထို့အပြင်၊ စာရင်းအင်းဖြန့်ဝေမှု၏ပျမ်းမျှသည် ၎င်း၏သင်္ချာဆိုင်ရာမျှော်လင့်ချက်နှင့် ညီမျှသည်။

ပျမ်းမျှဥပမာ

ကျောင်းသားတစ်ဦးသည် စာသင်နှစ်တွင် အောက်ပါအဆင့်များကို အောင်မြင်ခဲ့သည်- သင်္ချာ ၉၊ ဘာသာစကား ၇၊ သမိုင်း ၆၊ ဘောဂဗေဒ ၈ နှင့် သိပ္ပံ ၇.၅။ မင်းရဲ့အဆင့်အားလုံးရဲ့ ပျမ်းမျှက ဘယ်လောက်လဲ။

ဂဏန်းသင်္ချာပျှမ်းမျှကိုရှာရန်၊ ကျွန်ုပ်တို့သည် အတန်းအားလုံးကိုပေါင်း၍ သင်တန်းရှိ ဘာသာရပ်စုစုပေါင်းအရေအတွက်အားဖြင့် 5 ဖြစ်သည့် ဂဏန်းဖြင့် ပိုင်းခြားရန် လိုအပ်ပါသည်။ ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် ဂဏန်းသင်္ချာပျမ်းမျှဖော်မြူလာကို အသုံးပြုသည်-

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^N x_i}{N}$

ကျွန်ုပ်တို့သည် ဒေတာကို ဖော်မြူလာတွင် အစားထိုးပြီး ဂဏန်းသင်္ချာဆိုလိုအား တွက်ချက်သည်-

$\overline{x}=\cfrac{9+7+5+8+7,5}{5}=7,3$

သင်တွေ့မြင်ရသည့်အတိုင်း ဂဏန်းသင်္ချာပျှမ်းမျှတွင်၊ တန်ဖိုးတစ်ခုစီအတွက် တူညီသောအလေးချိန်ကို သတ်မှတ်ထားသည်၊ ဆိုလိုသည်မှာ ဒေတာအပိုင်းတစ်ခုစီတွင် အလေးချိန်တူညီပါသည်။

မီဒီယံ

ပျမ်းမျှ သည် အသေးဆုံးမှ အကြီးဆုံးသို့ စီထားသော ဒေတာအားလုံး၏ အလယ်တန်ဖိုးဖြစ်သည်။ တစ်နည်းဆိုရသော် အလယ်အလတ်သည် သတ်မှတ်ထားသော ဒေတာများကို အညီအမျှ နှစ်ပိုင်းခွဲသည်။

ပျမ်းမျှ တွက်ချက်မှုသည် ဒေတာ စုစုပေါင်း အရေအတွက်သည် လုံးခြင်း သို့မဟုတ် ထူးဆန်းခြင်း ရှိမရှိအပေါ် မူတည်သည်-

ဒေတာစုစုပေါင်းအရေအတွက်သည် ထူးဆန်း ပါက၊ ပျမ်းမျှသည် ဒေတာ၏အလယ်တွင် ညာဘက်ကျရောက်သည့်တန်ဖိုးဖြစ်သည်။ ဆိုလိုသည်မှာ စီထားသောဒေတာ၏ အနေအထား (n+1)/2 တွင်ရှိသော တန်ဖိုးကို ဆိုလိုခြင်းဖြစ်သည်။

$Me=x_{\frac{n+1}{2}$

ဒေတာအချက်များ စုစုပေါင်းအရေအတွက်သည် တူညီ ပါက၊ အလယ်ဗဟိုတွင်ရှိသော ဒေတာအချက်နှစ်ချက်၏ ပျမ်းမျှဖြစ်လိမ့်မည်။ ဆိုလိုသည်မှာ မှာယူထားသော ဒေတာ၏ ရာထူး n/2 နှင့် n/2+1 တွင် တွေ့ရသည့် ဂဏန်းသင်္ချာပျမ်းမျှတန်ဖိုးများကို ဆိုလိုသည်။

$Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$

ရွှေ

$n$

နမူနာရှိ အချက်အလက် စုစုပေါင်း အရေအတွက် ဖြစ်သည် ။

Me ဟူသော အသုံးအနှုန်းကို တန်ဖိုးတစ်ခုသည် ရှုမြင်မှုအားလုံး၏ အလယ်ဗဟိုဖြစ်ကြောင်း ညွှန်ပြရန်အတွက် သင်္ကေတတစ်ခုအဖြစ် အသုံးပြုလေ့ရှိသည်။

အလယ်အလတ် ဥပမာ

အောက်ပါဒေတာများ၏ အလယ်ဗဟိုကို ရှာပါ- 3၊ 4၊ 1၊ 6၊ 7၊ 4၊ 8၊ 2၊ 8၊ 4၊ 5

တွက်ချက်ခြင်းမပြုမီ ပထမဆုံးလုပ်ဆောင်ရမည့်အချက်မှာ အချက်အလက်များကို အမျိုးအစားခွဲရန်ဖြစ်ပြီး၊ ဆိုလိုသည်မှာ ကျွန်ုပ်တို့သည် နံပါတ်များကို အငယ်ဆုံးမှ အကြီးဆုံးသို့ ထားခြင်းဖြစ်သည်။

$1 \ 2 \ 3 \ 4 \ 4 \ 4 \ 5 \ 6 \ 7 \ 8 \ 8$

ဤကိစ္စတွင် ကျွန်ုပ်တို့တွင် လေ့လာသုံးသပ်ချက် ၁၁ ခုရှိသည်၊ ထို့ကြောင့် စုစုပေါင်းဒေတာသည် ထူးဆန်းသည်။ ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် အလယ်တန်း၏ အနေအထားကို တွက်ချက်ရန် အောက်ပါဖော်မြူလာကို အသုံးပြုပါသည်။

$\cfrac{n+1}{2}=\cfrac{11+1}{2}=6$

ထို့ကြောင့် အလယ်အလတ်သည် ဆဋ္ဌမအနေအထားတွင်ရှိသော ဒေတာဖြစ်မည်ဖြစ်ပြီး၊ ဤကိစ္စတွင် တန်ဖိုး 4 နှင့် ကိုက်ညီသည်။

$Me=x_6=4$

ဖက်ရှင်

စာရင်းဇယားများတွင်၊ မုဒ် သည် အမြင့်ဆုံး ပကတိကြိမ်နှုန်းပါရှိသော ဒေတာအစုံတွင် တန်ဖိုးဖြစ်သည်၊ ဆိုလိုသည်မှာ မုဒ်သည် ဒေတာအတွဲတစ်ခုတွင် ထပ်ခါတလဲလဲ အများဆုံးတန်ဖိုးဖြစ်သည်။

ထို့ကြောင့်၊ ကိန်းဂဏန်းအချက်အလက်အစုတစ်ခု၏ မုဒ်ကို တွက်ချက်ရန်၊ နမူနာတွင် ဒေတာဒြပ်စင်တစ်ခုစီတွင် ပေါ်လာသည့်အကြိမ်အရေအတွက်ကို ရိုးရိုးရေတွက်ပြီး ထပ်ခါတလဲလဲ အများဆုံးဒေတာသည် မုဒ်ဖြစ်လိမ့်မည်။

မုဒ်ကို စာရင်းအင်းမုဒ် သို့မဟုတ် မော်ဒယ်တန်ဖိုး ဟုလည်း ဆိုနိုင်သည်။ အလားတူ၊ ဒေတာကို ကြားကာလများအဖြစ် အုပ်စုဖွဲ့သည့်အခါ၊ ထပ်ခါတလဲလဲ ကြားကာလ အများဆုံးမှာ modal interval သို့မဟုတ် modal class ဖြစ်သည်။

ယေဘူယျအားဖြင့်၊ Mo ဟူသော အသုံးအနှုန်းကို ကိန်းဂဏန်းမုဒ်အတွက် သင်္ကေတအဖြစ် အသုံးပြုသည်၊ ဥပမာ၊ ဖြန့်ဖြူးမှုမုဒ် X သည် Mo(X) ဖြစ်သည်။

ထပ်ခါတလဲလဲ အများဆုံးတန်ဖိုးများအလိုက် မုဒ်သုံးမျိုးခွဲခြားနိုင်သည်-

Unimodal မုဒ် : ထပ်ခါတလဲလဲ အများဆုံးအကြိမ်အရေအတွက် တစ်ခုတည်းသာရှိသည်။ ဥပမာ၊ [၁၊ ၄၊ ၂၊ ၄၊ ၅၊ ၃]။
Bimodal မုဒ် : ထပ်ခါတလဲလဲ အများဆုံးအကြိမ်အရေအတွက်သည် မတူညီသောတန်ဖိုးနှစ်ခုတွင် ဖြစ်ပေါ်ပြီး တန်ဖိုးနှစ်ခုစလုံးသည် အကြိမ်အရေအတွက် တူညီပါသည်။ ဥပမာ၊ [၂၊ ၆၊ ၇၊ ၂၊ ၃၊ ၆၊ ၉]။
Multimodal မုဒ် – သုံးမျိုး သို့မဟုတ် ထို့ထက်ပိုသော တန်ဖိုးများသည် ထပ်ခါတလဲလဲ အများဆုံးအကြိမ်အရေအတွက် တူညီသည်။ ဥပမာ၊ [၃၊ ၃၊ ၄၊ ၁၊ ၃၊ ၄၊ ၂၊ ၁၊ ၄၊ ၅၊ ၂၊ ၁]။

ဖက်ရှင်ဥပမာ

အောက်ပါဒေတာအတွဲ၏မုဒ်မှာ အဘယ်နည်း။

$5 \ 4 \ 9 \ 7 \ 2 \ 3 \ 9 \ 6 \ 5 \ 2 \ 5$

နံပါတ်များသည် အစဉ်လိုက်ဖြစ်နေသောကြောင့် ကျွန်ုပ်တို့ ပထမဆုံးလုပ်ရမည့်အရာမှာ ၎င်းတို့ကို စီပါ။ ဤအဆင့်သည် မဖြစ်မနေ မလိုအပ်သော်လည်း ဖက်ရှင်ကို ပိုမိုလွယ်ကူစွာ ရှာဖွေနိုင်မည်ဖြစ်သည်။

$2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 7 \ 9 \ 9$

နံပါတ် 2 နှင့် 9 သည် နှစ်ကြိမ်ပေါ်လာသော်လည်း 5 သည် သုံးကြိမ်ထပ်ခါထပ်ခါဖြစ်သည်။ ထို့ကြောင့်၊ ဒေတာစီးရီး၏မုဒ်မှာ နံပါတ် ၅ ဖြစ်သည်။

$Mo=5$

ပျမ်းမျှ၊ အလယ်အလတ် နှင့် မုဒ် လေ့ကျင့်ခန်းကို ဖြေရှင်းထားသည်။

ယခု သင်ဆိုလိုအား၊ အလယ်အလတ်နှင့် မုဒ်တို့သည် မည်ကဲ့သို့ဖြစ်သည်ကို သင်သိပြီးဖြစ်၍ အောက်တွင်ဖော်ပြထားသော ကိန်းဂဏန်းဆိုင်ရာတိုင်းတာမှုများအပေါ် အသေးစိပ်လေ့ကျင့်ခန်းတစ်ခုဖြစ်ပြီး ၎င်းတို့ကို မည်ကဲ့သို့တွက်ချက်ထားသည်ကို သင်အတိအကျသိနိုင်မည်ဖြစ်သည်။

အောက်ပါစာရင်းအင်းဒေတာအတွဲ၏ ပျမ်းမျှ၊ ပျမ်းမျှနှင့် မုဒ်ကို ရှာပါ-

$8 \ 7 \ 0 \ 6 \ 10 \ 9 \ 13 \ 8 \ 0 \ 6 \ 2 \ 6 \ 5 \ 11 \ 10$

$0 \ 9 \ 8 \ 6 \ 12 \ 3 \ 5 \ 11 \ 1 \ 4 \ 8 \ 10 \ 2 \ 5 \ 7$

ဒေတာ၏ ပျမ်းမျှအား ရှာဖွေရန်၊ ၎င်းကို ပေါင်းထည့်ရန် လိုအပ်ပြီး ဒေတာ စုစုပေါင်း အရေအတွက်ကို 30 ဖြင့် ပိုင်းခြားရန် လိုအပ်သည်-

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^N x_i}{N}=\frac{192}{30}=6,4$

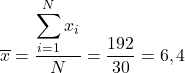
ဒုတိယ၊ နမူနာ အလယ်အလတ်ကို ရှာကြည့်ရအောင်။ ထို့ကြောင့် ကျွန်ုပ်တို့သည် ဂဏန်းအားလုံးကို ကြီးစဉ်ငယ်လိုက် ထားလိုက်သည်-

$0 \ 0 \ 0 \ 1 \ 2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 6 \ 6 \ 6$

$7 \ 7 \ 8 \ 8 \ 8 \ 8 \ 9 \ 9 \ 10 \ 10 \ 10 \ 11 \ 11 \ 12 \ 13$

ဤကိစ္စတွင်၊ ဒေတာစုစုပေါင်းအရေအတွက်သည် ညီနေသောကြောင့် အလယ်အလတ်ကိုတွေ့ရှိမည့် ဗဟိုရာထူးနှစ်ခုကို တွက်ချက်ရန် လိုအပ်ပါသည်။ ယင်းအတွက် ကျွန်ုပ်တို့သည် အောက်ပါဖော်မြူလာနှစ်ခုကို အသုံးပြုပါသည်။

$\cfrac{n}{2}=\cfrac{30}{2}=15$

$\cfrac{n}{2}+1=\cfrac{30}{2}+1=16$

ထို့ကြောင့် ပျမ်းမျှသည် တန်ဖိုး 6 နှင့် 7 တို့နှင့် အသီးသီးသက်ဆိုင်သည့် ဆယ်ငါးခုနှင့် တစ်ဆယ့်ခြောက်အနေအထားကြားတွင် ရှိနေမည်ဖြစ်သည်။ ပို၍တိကျစွာပြောရလျှင် ပျမ်းမျှသည် ဤတန်ဖိုးများ၏ ပျမ်းမျှနှင့် ညီမျှသည်-

$Me=\cfrac{x_{15}+x_{16}}{2}=\cfrac{6+7}{2}=6,5$

နောက်ဆုံးအနေဖြင့်၊ မုဒ်ကိုရှာရန် နံပါတ်တစ်ခုစီပေါ်လာသည့်အချိန်အားလုံးကို ရေတွက်ရန်သာလိုသည်။ သင်တွေ့မြင်ရသည့်အတိုင်း နံပါတ် ၆ နှင့် နံပါတ် ၈ သည် စုစုပေါင်းအကြိမ်ရေ လေးကြိမ်ပေါ်လာသည်၊ ယင်းသည် အများဆုံးအကြိမ်ကြိမ်ဖြစ်သည်။ ထို့ကြောင့်၊ ဤကိစ္စတွင်၊ ၎င်းသည် bimodal မုဒ်ဖြစ်ပြီး နံပါတ်နှစ်ခုသည် dataset ၏မုဒ်ဖြစ်သည်။

$Mo=\{ 6 \ ; \ 8\}$

ပျမ်းမျှ၊ ပျမ်းမျှနှင့် မုဒ်ဂဏန်းတွက်စက်

၎င်း၏ပျမ်းမျှ၊ ပျမ်းမျှနှင့် မုဒ်ကိုတွက်ချက်ရန် အောက်ပါအွန်လိုင်းဂဏန်းတွက်စက်ထဲသို့ စာရင်းအင်းနမူနာတစ်ခုခုမှဒေတာကို ထည့်သွင်းပါ။ ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။