ပျမ်းမျှအလေးချိန်

အားဖြင့် Benjamin Anderson ဩဂုတ် 6, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤတွင် ကျွန်ုပ်တို့သည် ပျမ်းမျှအလေးချိန်ကို မည်ကဲ့သို့ တွက်ချက်သည်ကို ရှင်းပြပါသည်။ ကျွန်ုပ်တို့သည် ကိုယ်အလေးချိန်ပျမ်းမျှကို မည်သို့ရှာဖွေကြောင်း ဖြေရှင်းထားသော လေ့ကျင့်ခန်းကို သင်တွေ့မြင်နိုင်မည်ဖြစ်သည်။ ထို့အပြင်၊ အဆုံးတွင် ဂဏန်းပေါင်းစက်ဖြင့် မည်သည့်ဒေတာအတွဲ၏ အလေးချိန်ပျမ်းမျှကို တွက်ချက်နိုင်သည်။

အလေးချိန်ပျမ်းမျှဆိုတာဘာလဲ။

အလေးချိန်ပျမ်းမျှသည် သရုပ်ဖော်ကိန်းဂဏန်းများ၏ ဗဟိုအချက်အချာကျသော အတိုင်းအတာတစ်ခုဖြစ်သည်။ ကိုယ်အလေးချိန် ပျမ်းမျှကို တွက်ချက်ရန်၊ ကိန်းဂဏန်း အချက်အလက် တစ်ခုစီကို ၎င်း၏ အလေးချိန် (သို့မဟုတ်) အလေးချိန် ဖြင့် ဦးစွာ မြှောက်ပြီး ထုတ်ကုန် အားလုံးကို ပေါင်းထည့်ကာ နောက်ဆုံးတွင် အလေးချိန် ပေါင်းလဒ်ကို အလေးများအားလုံး၏ ပေါင်းလဒ်ဖြင့် ပိုင်းခြားရပါမည်။

တစ်နည်းဆိုရသော် အလေးချိန်ပျမ်းမျှအတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်။

x _i သည် ဒေတာနမူနာတစ်ခုစီကို ကိုယ်စားပြုပြီး ၎င်း _{နှင့်} သက်ဆိုင်သောအလေးချိန်။

ထို့ကြောင့်၊ ဒေတာအပိုင်းတစ်ခု၏ အလေးချိန် ပိုများလေ၊ အလေးချိန် ပျမ်းမျှတွက်ချက်မှုတွင် ၎င်းသည် ပို၍အရေးကြီးပါသည်။ တစ်နည်းဆိုရသော် ဒေတာအပိုင်းတစ်ခု၏ အလေးချိန် ပိုများလေ၊ ၎င်းသည် အလေးချိန် ပျမ်းမျှရလဒ်အပေါ် လွှမ်းမိုးနိုင်လေဖြစ်သည်။

ကိုယ်အလေးချိန် ပျမ်းမျှသည် အဆင့်များကို တွက်ချက်ရာတွင် အထူးအသုံးဝင်သည်၊ အဘယ်ကြောင့်ဆိုသော် ၎င်းသည် သင်တန်းတစ်ခုအတွင်း ပြုလုပ်ခဲ့သော လေ့ကျင့်ခန်း သို့မဟုတ် စာမေးပွဲများကို မတူညီသော အရေးပါမှုဖြင့် အကဲဖြတ်နိုင်စေသောကြောင့် ဖြစ်သည်။ လူဦးရေ၏စျေးနှုန်းများကိုတိုင်းတာရန်အတွက်ညွှန်ပြချက်တစ်ခုဖြစ်သည့် CPI (စားသုံးသူစျေးနှုန်းညွှန်းကိန်း) ကိုတွက်ချက်ရာတွင်လည်းအလေးချိန်ပျမ်းမျှပျမ်းမျှကိုအသုံးပြုသည်။

အလေးချိန်ပျမ်းမျှအပြင်၊ ဂျီဩမေတြီပျမ်းမျှ၊ ဂဏန်းသင်္ချာပျမ်းမျှ၊ စတုရန်းပျှမ်းမျှနှင့် ဟာမိုနစ်ပျမ်းမျှကဲ့သို့သော အခြားပျမ်းမျှအမျိုးအစားများလည်း ရှိသေးသည်။

ပျမ်းမျှအလေးချိန်ကို ဘယ်လိုတွက်မလဲ။

ပျမ်းမျှအလေးချိန်ကို တွက်ချက်ရန်အတွက် အောက်ပါအဆင့်များကို လိုက်နာရပါမည်-

ကိန်းဂဏန်းအချက်အလက်တစ်ခုစီကို ၎င်း၏သက်ဆိုင်ရာအလေးချိန်ဖြင့် မြှောက်ပါ။
ယခင်အဆင့်တွင်တွက်ချက်ထားသော ထုတ်ကုန်အားလုံးကို ပေါင်းထည့်ပါ။
အထက်တွင်ရှိသော အလေးချိန်ကို အလေးချိန်အားလုံး၏ပေါင်းလဒ်ဖြင့် ပိုင်းခြားပါ။
ရရှိသောရလဒ်မှာ ကိန်းဂဏန်းနမူနာ၏ ပျမ်းမျှအလေးချိန်ဖြစ်သည်။

👉 မည်သည့်ဒေတာအစုံ၏အလေးချိန်ပျမ်းမျှကိုတွက်ချက်ရန်အောက်ပါဂဏန်းတွက်စက်ကိုသင်အသုံးပြုနိုင်သည်။

အလေးချိန် ပျမ်းမျှ ဥပမာ

အလေးချိန်ပျမ်းမျှ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို ထည့်သွင်းစဉ်းစားခြင်းဖြင့် ဒေတာအစုတစ်ခုမှ အလေးချိန်ပျမ်းမျှအား မည်ကဲ့သို့ရယူသည်ကို အပြည့်အဝနားလည်ရန် ယခုလေ့ကျင့်ခန်းကို ကျွန်ုပ်တို့ ဖြေရှင်းပါမည်။

အထက်တန်းကျောင်း ပထမနှစ် ကျောင်းသားတစ်ဦးသည် သင်္ချာဘာသာရပ်တွင် အောက်ဖော်ပြပါ အဆင့်များကို ရရှိခဲ့သည်- တစ်ပိုင်းတစ်စ စာမေးပွဲတွင် 7 က 30%, 20% တန်ဖိုးရှိသော အုပ်စုအလုပ်တွင် 9 ခု၊ အတန်းထဲတွင် တွက်ဆထားသည့် လေ့ကျင့်ခန်းများတွင် 6 ခု၊ 10% နှင့် 40% အလေးချိန်ရှိသောနောက်ဆုံးစာမေးပွဲတွင် 8 ။ ဘာသာရပ်အတွက် မင်းရဲ့နောက်ဆုံးတန်းက ဘယ်လောက်လဲ။

ကျောင်းသား၏ အမှတ်အသားကို ဆုံးဖြတ်ရန်၊ ကြေငြာချက်မှ ပေးသော တန်ဖိုးများနှင့်အတူ အလေးချိန် ပျမ်းမျှကို ရှာရပါမည်။ ဒါကိုလုပ်ဖို့၊ ကိုယ်အလေးချိန် ပျမ်းမျှဖော်မြူလာကို သုံးပါတယ်။

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+x_3\cdot w_3+x_4\cdot w_4+x_5\cdot w_5}{w_1+w_2+w_3+w_4+w_5}$

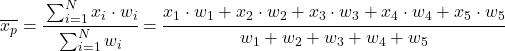
ပေးပို့နိုင်မှုတစ်ခုစီ၏ရမှတ်သည် ကိန်းဂဏန်းတန်ဖိုးဖြစ်ပြီး ၎င်း၏ရာခိုင်နှုန်းသည် ယင်းတန်ဖိုး၏အလေးချိန်နှင့် သက်ဆိုင်သည်။ ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် ဖော်မြူလာတွင် တန်ဖိုးများနှင့် အလေးများကို အစားထိုးပြီး အလေးချိန် ပျမ်းမျှတွက်ချက်မှုကို လုပ်ဆောင်သည်-

$\overline{x_p}=\cfrac{7\cdot 0,30+9\cdot 0,20+6\cdot 0,10+8\cdot 0,40}{0,30+0,20+0,10+0,40}=7,7$

ထို့ကြောင့် ဤကျောင်းသား၏ နောက်ဆုံးသင်္ချာအဆင့်သည် 7.7 ဖြစ်လိမ့်မည်

အလေးချိန် ပျမ်းမျှဂဏန်းတွက်စက်

၎င်း၏အလေးချိန်ပျမ်းမျှအား တွက်ချက်ရန် အောက်ဖော်ပြပါ ဂဏန်းပေါင်းစက်တွင် မည်သည့် ကိန်းဂဏန်းနမူနာနှင့် ၎င်းတို့၏ သက်ဆိုင်ရာ အလေးချိန်များမှ ဒေတာကို ထည့်သွင်းပါ။

ပထမအကွက်တွင် ကိန်းဂဏန်းအချက်အလက်များကို ဒုတိယအကွက်တွင် ၎င်းတို့၏ သက်ဆိုင်ရာအလေးချိန်များကို ထည့်သွင်းပါ။ အလေးများကို ဒေတာနှင့် ဒဿမဖော်မတ်ဖြင့် တူညီသောအစီအစဥ်ဖြင့် ရေးရပါမည်။ နံပါတ်များအားလုံးကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမ ခြားနားမှုအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

စံပြုအလေး

ကျွန်ုပ်တို့မြင်ခဲ့ရသည့်အတိုင်း၊ အလေးချိန် ပျမ်းမျှတွင်၊ အလေးချိန်သည် ၎င်းကို အနည်းနှင့်အများ ပေးရန်အတွက် အချက်အလက်တစ်ခုစီအတွက် ပေးထားသော တန်ဖိုးဖြစ်သည်။ ထို့ကြောင့် အချက်အလက်သည် အလွန်အရေးကြီးပါက၊ ၎င်းသည် အလွန်အလေးချိန် မြင့်မားလိမ့်မည်၊ သို့သော် အချက်အလက်များသည် အလွန်သက်ဆိုင်ခြင်းမရှိပါက၊ ၎င်းသည် အလွန်နည်းပါးသော အလေးချိန်ရှိသည်။

ကောင်းပြီ၊ ပုံမှန်အလေးချိန်သည် မည်သည့်အပိုင်းကိုမျှ လုပ်စရာမလိုဘဲ ပျမ်းမျှအလေးချိန်ရရှိရန် အသုံးပြုသည့် အလေးချိန်အမျိုးအစားတစ်ခုဖြစ်သည်။

ပုံမှန်အလေးချိန် ဆိုသည်မှာ အလေးချိန်အားလုံး၏ပေါင်းလဒ်ဖြင့် ပိုင်းခြားထားသော အချက်အလက်ပစ္စည်းတစ်ခု၏ အလေးချိန်ဖြစ်သည်။

$w_i'=\cfrac{w_i}{\sum_{k=1}^N w_k}$

ထို့ကြောင့် ပုံမှန်အလေးချိန်အားလုံး၏ ပေါင်းလဒ်သည် တစ်ခုနှင့် ညီမျှသည်-

$\sum_{i=1}^N w_i'=1$

ထို့ကြောင့်၊ ပုံမှန်အလေးချိန်များဖြင့် ပျမ်းမျှအလေးချိန်ကို တွက်ချက် ရန်၊ ဒေတာတစ်ခုစီကို ၎င်း၏ပုံမှန်အလေးချိန်ဖြင့် မြှောက်ပါ။

$\displaystyle\overline{x_p}=\sum_{i=1}^N x_i\cdot w_i'=x_1\cdot w_1'+x_2\cdot w_2'+\dots+x_N\cdot w_N'$

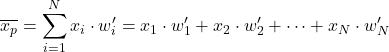
ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့တွင် ကိန်းဂဏန်းအချက်အလက်များသည် 24၊ 35၊ 17၊ 41 ရှိပြီး ၎င်းတို့၏ သက်ဆိုင်ရာအလေးချိန်များမှာ 4၊ 9၊ 6၊ 3 ဖြစ်သည်။ ဤဒေတာအစု၏ ပျမ်းမျှအလေးချိန်ကို ရှာဖွေရန်၊ ကျွန်ုပ်တို့သည် ပိုင်းခြားခြင်းဖြင့် ဦးစွာ ပုံမှန်အလေးချိန်များကို တွက်ချက်နိုင်ပါသည်။ အလေးချိန်တစ်ခုစီကို အလေးချိန်အားလုံး၏ ပေါင်းလဒ်အားဖြင့်၊

$\cfrac{4}{4+9+6+3}=0,18$

$\cfrac{9}{4+9+6+3}=0,41$

$\cfrac{6}{4+9+6+3}=0,27$

$\cfrac{3}{4+9+6+3}=0,14$

ယခု ဒေတာတစ်ခုစီကို ၎င်း၏ပုံမှန်အလေးချိန်ဖြင့် မြှောက်လိုက်ရုံဖြင့် ရလဒ်သည် အလေးချိန်ပျမ်းမျှဖြစ်လိမ့်မည်-

$\overline{x_p}=24\cdot 0,18+35\cdot 0,41+17\cdot 0,27+41\cdot 0,14=28,91$

အလေးချိန်ပျမ်းမျှနှင့် ဂဏန်းသင်္ချာပျမ်းမျှအကြား ကွာခြားချက်

အလားတူ လုပ်ဆောင်ချက်များကို လုပ်ဆောင်ရမည်ဖြစ်သောကြောင့် အလေးချိန် ပျမ်းမျှနှင့် ဂဏန်းသင်္ချာပျမ်းမျှအား တွက်ချက်ရာတွင် တူညီသောနည်းလမ်းဖြင့် လုပ်ဆောင်ပါသည်။ အလေးချိန် ပျမ်းမျှအားဖြင့် ဒေတာအမှတ်တစ်ခုစီကို ၎င်း၏အလေးချိန်ဖြင့် မြှောက်ပြီး အလေးချိန်၏ပေါင်းလဒ်ဖြင့် ပိုင်းခြားသော်လည်း ဂဏန်းသင်္ချာပျှမ်းမျှအားဖြင့် ဒေတာအားလုံးကို ပေါင်းပြီး ဒေတာစုစုပေါင်းအရေအတွက်ဖြင့် ပိုင်းခြားထားသည်။

အလေးချိန် ပျမ်းမျှနှင့် ဂဏန်းသင်္ချာပျှမ်းမျှအကြား ကွာခြားချက်မှာ ၎င်း၏ အယူအဆတွင် တည်ရှိသည်၊ ဂဏန်းသင်္ချာ ပျမ်းမျှတွင် ဒေတာအားလုံးသည် တူညီသောတန်ဖိုးရှိသည်ဟု ယူဆသောကြောင့်၊ သို့သော် အလေးချိန် ပျမ်းမျှတွင် ဒေတာတစ်ခုစီတွင် အလေးချိန်ကွဲပြားသည်။

အလေးချိန်အားလုံး ညီမျှပါက အလေးချိန်ပျမ်းမျှသည် ဂဏန်းသင်္ချာပျမ်းမျှနှင့် ညီမျှကြောင်း သတိပြုပါ။ သင်္ချာဆိုင်ရာ အထောက်အထားကို အောက်တွင် ကြည့်ရှုနိုင်ပါသည်။

$\begin{aligned}\overline{x_p}&=\cfrac{x_1\cdot w+x_2\cdot w+x_3\cdot w+\dots+x_N\cdot w}{w+w+w+\dots +w}\\[2ex]&= \cfrac{w\cdot (x_1+x_2+\dots+x_N)}{N\cdot w}=\\[2ex] &= \cfrac{x_1+x_2+\dots+x_N}{N}=\overline{x}\end{aligned}$

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။