Excel တွင် central limit theorem ကို ဘယ်လိုအသုံးချမလဲ။

လူဦးရေ ဖြန့်ဝေမှုသည် ပုံမှန်မဟုတ်သော်လည်း နမူနာအရွယ်အစားသည် ပုံမှန်မဟုတ်လျှင်ပင် အလယ်အလတ်ကန့်သတ်သီအိုရီက နမူနာဆိုလိုးဖြန့်ဝေမှုသည် ခန့်မှန်းခြေအား ဖြင့် ပုံမှန်ဖြစ်ကြောင်း ဖော်ပြထားသည်။

ဗဟိုကန့်သတ်သီအိုရီတွင်လည်း နမူနာဖြန့်ဝေမှုတွင် အောက်ပါဂုဏ်သတ္တိများ ပါလိမ့်မည်-

1. နမူနာဖြန့်ဝေမှု၏ပျမ်းမျှသည် လူဦးရေဖြန့်ဖြူးမှု၏ပျမ်းမျှနှင့် ညီမျှသည်-

x = µ

2. နမူနာ ဖြန့်ဝေမှု၏ စံသွေဖည်မှုသည် နမူနာအရွယ်အစားဖြင့် ပိုင်းခြားထားသော လူဦးရေ စံသွေဖည်မှုနှင့် ညီမျှသည်-

s = σ / √n

ဤသင်ခန်းစာတွင် Excel တွင် ဗဟိုကန့်သတ်သီအိုရီကို ပေးထားသော ဖြန့်ဖြူးမှုတွင် မည်သို့အသုံးပြုရမည်ကို ရှင်းပြထားသည်။

Excel တွင် Central Limit Theorem ကိုအသုံးပြုခြင်း။

ကျွန်ုပ်တို့တွင် ပျမ်းမျှ 8 နှင့် စံသွေဖည်မှု 4 ရှိသော ဖြန့်ဖြူးမှုတစ်ခုရှိသည်ဆိုပါစို့။ နမူနာအရွယ်အစား 15 ဖြင့် နမူနာဖြန့်ဝေခြင်း၏ ပျမ်းမျှနှင့် စံသွေဖည်မှုကို ရှာဖွေရန် Excel တွင် အောက်ပါဖော်မြူလာများကို အသုံးပြုနိုင်ပါသည်။

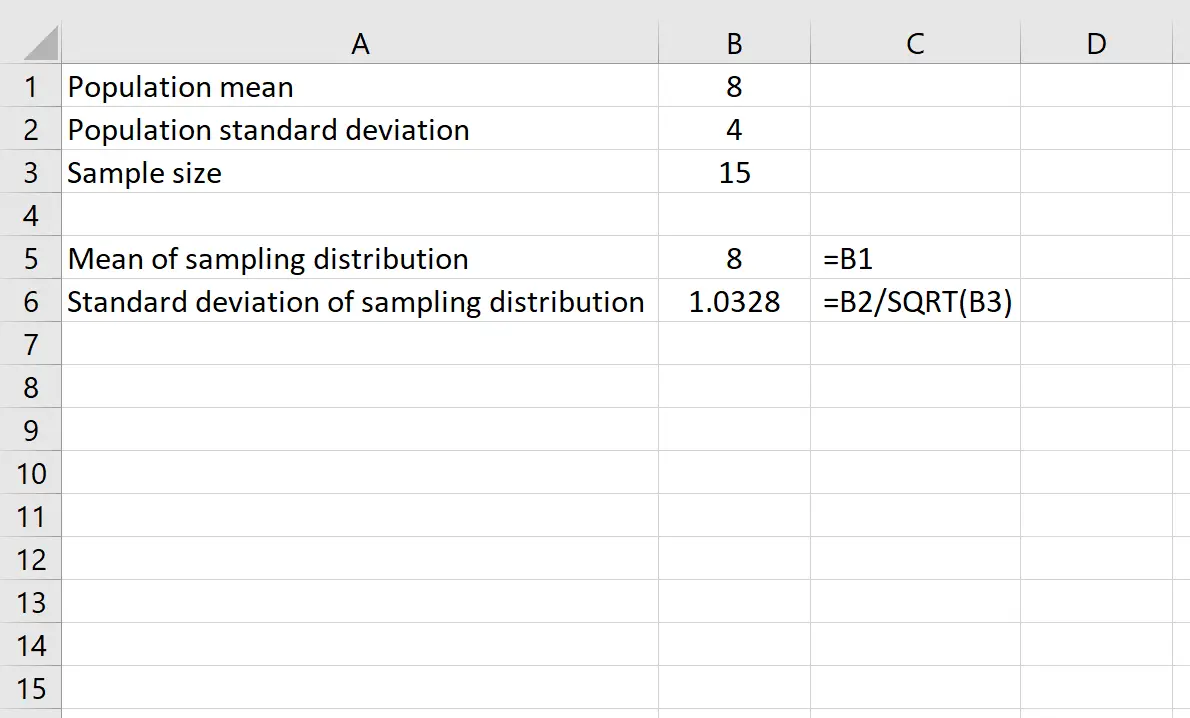
နမူနာဖြန့်ဝေမှု၏ပျမ်းမျှသည် 8 ဖြစ်သည့် လူဦးရေဖြန့်ဖြူးမှု၏ပျမ်းမျှနှင့်ညီမျှသည်။

နမူနာ ဖြန့်ဝေမှု၏ စံသွေဖည်မှုသည် နမူနာအရွယ်အစားဖြင့် ပိုင်းခြားထားသော လူဦးရေစံသွေဖည်မှုနှင့် ညီသည်၊ သို့မဟုတ်- 4 /√15 = 1.0328 ။

ဖြစ်နိုင်ခြေဆိုင်ရာမေးခွန်းများကိုဖြေဆိုရန် ဗဟိုကန့်သတ်သီအိုရီကိုလည်း အသုံးပြုနိုင်သည်။ ဥပမာအားဖြင့်၊ ပေးထားသောလူဦးရေတွင် ပျမ်းမျှ 8 နှင့် 4 ၏ စံသွေဖည်ပါက၊ ပေးထားသော အရွယ်အစား နမူနာ 15 ၏ ဖြစ်နိုင်ခြေမှာ အဘယ်နည်း။   ပျမ်းမျှ 7 နှင့် ညီမျှသည် ?

ဤမေးခွန်းကိုဖြေဆိုရန်၊ အောက်ပါ syntax ကိုအသုံးပြုသည့် Excel တွင် NORM.DIST() လုပ်ဆောင်ချက်ကို အသုံးပြုနိုင်ပါသည်။

NORM.DIST(x၊ ပျမ်းမျှ၊ standard_dev၊ စုစည်းမှု)

ရွှေ-

• x : နမူနာဆိုလိုသည်မှာ စမ်းသပ်လိုခြင်းဖြစ်သည်။
• ဆိုလိုချက်- နမူနာဖြန့်ချီမှု၏ မျှော်မှန်းထားချက်
• standard_dev- နမူနာ ဖြန့်ချီမှု၏ မျှော်မှန်းထားသော စံသွေဖည်မှု
• စုစည်းမှု- TRUE သည် ပုံမှန် CDF တန်ဖိုးကို ပြန်ပေးသည်။ FALSE သည် ပုံမှန် PDF ၏ တန်ဖိုးကို ပြန်ပေးသည်။ ကျွန်ုပ်တို့၏အခြေအနေတွင်၊ ကျွန်ုပ်တို့သည် TRUE ကို အမြဲသုံးပါမည်။

ဤလုပ်ဆောင်ချက်သည် နမူနာဆိုလိုချက်သည် အချို့သောတန်ဖိုးထက် နည်းသော သို့မဟုတ် ညီမျှသည့် ဖြစ်နိုင်ခြေကို ပြန်ပေးလိမ့်မည်။

ဤဥပမာတွင်ကျွန်ုပ်တို့အသုံးပြုမည့်ဖော်မြူလာသည်

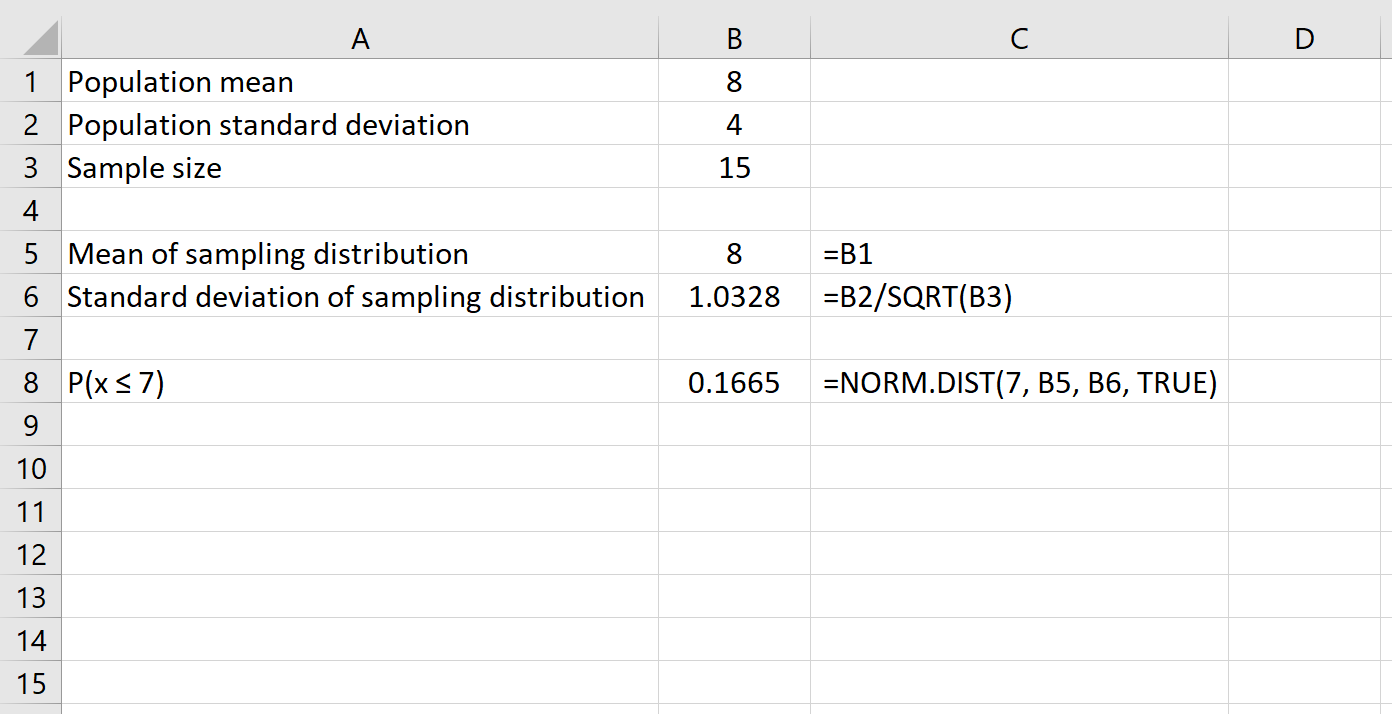
၎င်းသည် ကျွန်ုပ်တို့အား ပျမ်းမျှ 8 နှင့် 4 ၏ စံသွေဖည်သော လူဦးရေအတွက် အရွယ်အစား 15 နမူနာကို ပေးထားသည့် ဖြစ်နိုင်ခြေ   ပျမ်းမျှ 7 သို့မဟုတ် 0.1665 ထက်နည်းသည် သို့မဟုတ် ညီမျှသည်။

ဖော်မြူလာ 1 – NORM.DIST() ကို သုံးရုံဖြင့် ပေးထားသောနမူနာအရွယ်အစားသည် သတ်မှတ်ထားသော နံပါတ်ထက် အဓိပ္ပါယ် ပိုကြီးလိမ့် မည်ဟူသော ဖြစ်နိုင်ခြေကိုလည်း ကျွန်ုပ်တို့ ရှာဖွေနိုင်သည်။

ဥပမာအားဖြင့်၊ အောက်ပါပုံသေနည်းသည် ပေးထားသောနမူနာအရွယ်အစား 15 ၏ဖြစ်နိုင်ခြေကို 7 ထက်ပို၍ ပျမ်းမျှရှိမည်ကို မည်သို့ဆုံးဖြတ်ရမည်ကို ပြသသည်-

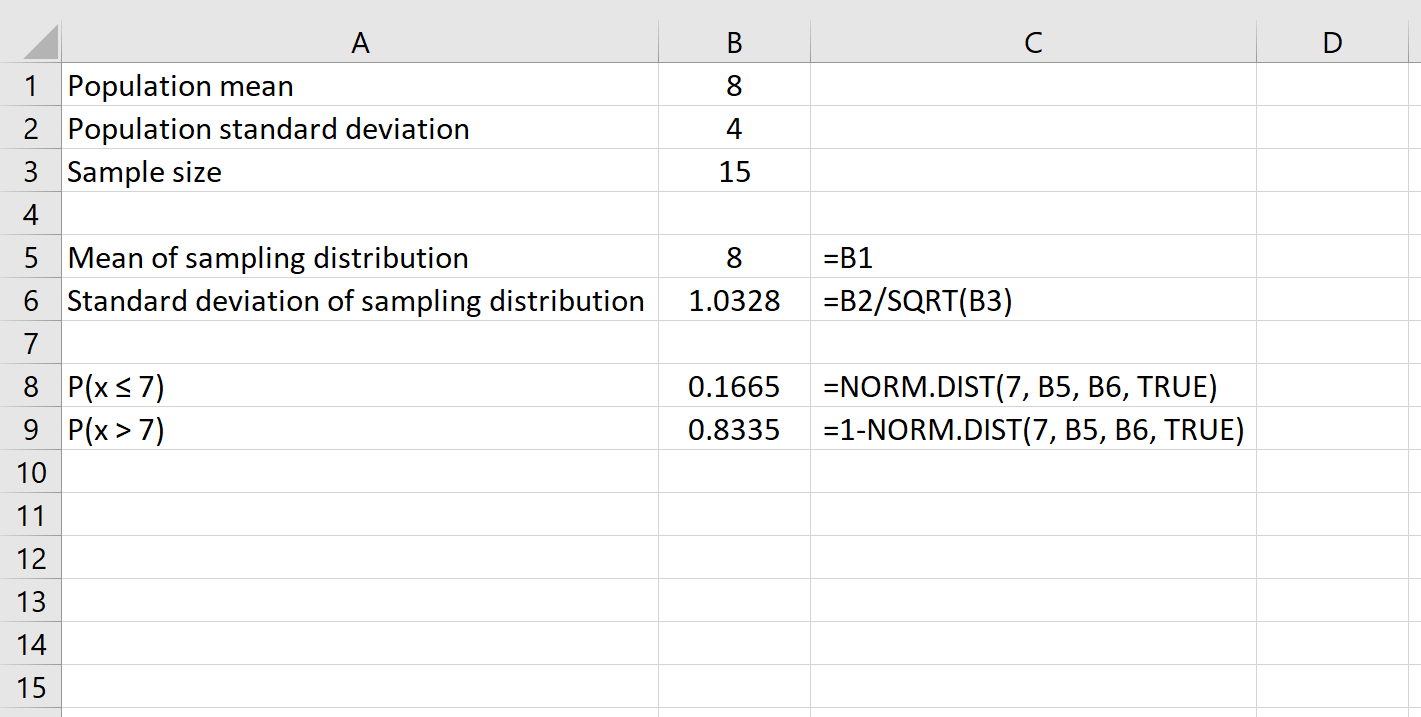
နောက်ဆုံးတွင်၊ ပေးထားသောနမူနာအရွယ်အစား သည် NORM.DIST(ပိုကြီးသောနံပါတ်) – NORM.DIST(အသေးစားနံပါတ်) ဖော်မြူလာကို အသုံးပြု၍ ဂဏန်းနှစ်လုံး ကြားတွင် အဓိပ္ပါယ်ရှိကြောင်း ဖြစ်နိုင်ခြေကို ကျွန်ုပ်တို့ ရှာတွေ့နိုင်ပါသည်။

ဥပမာအားဖြင့်၊ အောက်ပါပုံသေနည်းသည် ပေးထားသောနမူနာအရွယ်အစား 15 တွင် 7 နှင့် 9 အကြား ပျမ်းမျှရှိကြောင်း ဖြစ်နိုင်ခြေကို မည်သို့ရှာဖွေရမည်ကို ပြသသည်-

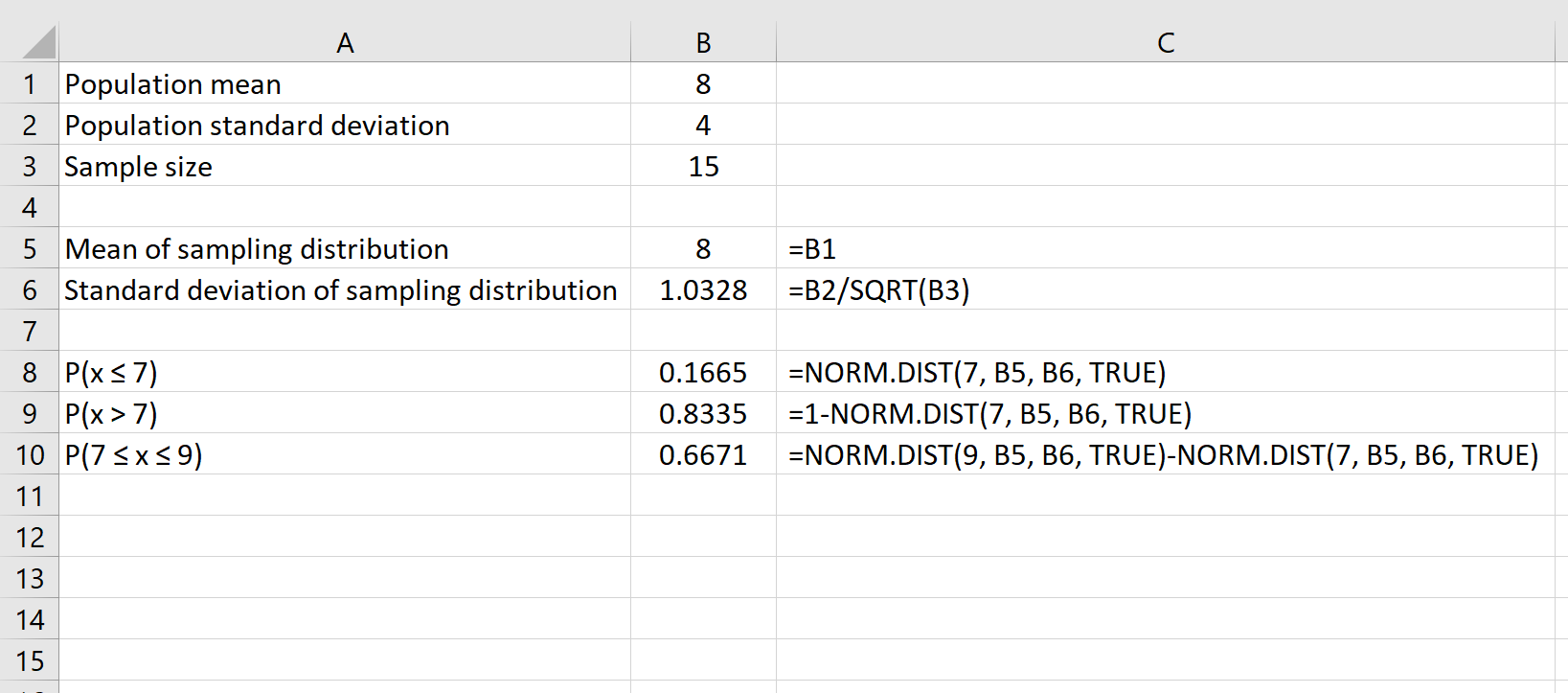
ထပ်လောင်းအရင်းအမြစ်များ

Central Limit Theorem ဂဏန်းတွက်စက်
Excel တွင် လက်မ၏ စည်းကမ်းကို မည်သို့ကျင့်သုံးမည်နည်း။
Excel တွင် Bell Curve ဖန်တီးနည်း