ဗဟိုကန့်သတ်သီအိုရီ

အားဖြင့် Benjamin Anderson ဩဂုတ် 1, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် ဗဟိုကန့်သတ်သီအိုရီ (CLT) သည် အဘယ်အရာနှင့် ၎င်းကို စာရင်းအင်းများတွင် အသုံးပြုကြောင်း ရှင်းပြထားသည်။ ဗဟိုကန့်သတ်သီအိုရီ၏ ဖော်မြူလာဖြစ်သည့် ဖော်မြူလာနှင့် ၎င်း၏ အပလီကေးရှင်း၏ နမူနာကို အဆင့်ဆင့် ဖြေရှင်းထားသည်ကိုလည်း တွေ့ရပါမည်။

ဗဟိုကန့်သတ်သီအိုရီဆိုတာ ဘာလဲ။

စာရင်းဇယားများတွင်၊ ဗဟိုကန့်သတ်သီအိုရီ ( central limit theorem) ဟုလည်း ခေါ်သည် ၊ နမူနာဖြန့်ဝေမှုသည် လူဦးရေ၏ ဖြစ်နိုင်ခြေ ဖြန့်ဝေမှု မည်သို့ပင်ရှိစေကာမူ နမူနာ အရွယ်အစား တိုးလာသည်နှင့်အမျှ ပုံမှန် ဖြန့်ဖြူးမှုသို့ ချဉ်းကပ်သည်ဟု ဖော်ပြထားသည်။

ဆိုလိုသည်မှာ၊ ကျွန်ုပ်တို့သည် လုံလောက်သော အရေအတွက်နမူနာများကို ယူပါက၊ ထိုနမူနာများ၏ ပျမ်းမျှအား ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခုအဖြစ် ခန့်မှန်းနိုင်သည်ဟု ဆိုလိုပါသည်။

ထို့အပြင်၊ နမူနာအရွယ်အစားသည် နမူနာအရွယ်အစား တိုးလာသည်နှင့်အမျှ လူဦးရေ၏ ဆိုလိုရင်းတန်ဖိုးသို့ ချဉ်းကပ်သွားမည်ဖြစ်ကြောင်း ဗဟိုကန့်သတ်သီအိုရီက ဖော်ပြသည်။ ၎င်းသည် ကျွန်ုပ်တို့အား စာရင်းအင်းလူဦးရေ၏ ကန့်သတ်ချက်များကို ခန့်မှန်းနိုင်စေပါသည်။ အောက်တွင် ကျွန်ုပ်တို့ မည်သို့လုပ်ဆောင်သည်ကို တွေ့ရမည်ဖြစ်ပါသည်။

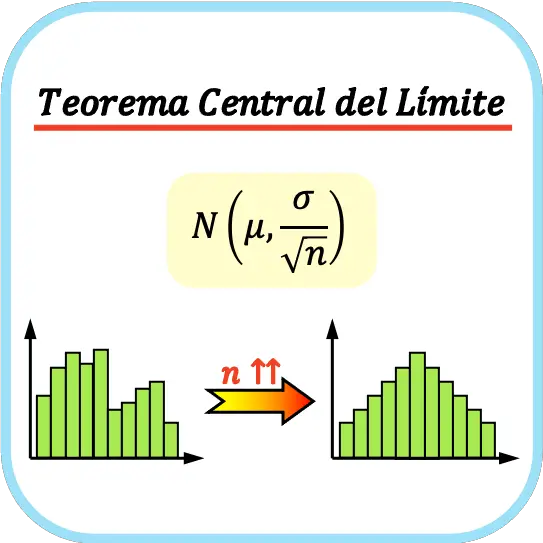
ယေဘူယျအားဖြင့်၊ ဗဟိုကန့်သတ်သီအိုရီကို ကျင့်သုံးရန်၊ နမူနာအရွယ်အစားသည် လေ့လာထားသော ကိန်းရှင်၏ဝိသေသလက္ခဏာများပေါ်တွင်မူတည်သော်လည်း ၎င်းသည် အနည်းဆုံး လေ့လာတွေ့ရှိချက် 30 ရှိရမည်ဟု ယူဆပါသည်။

ဗဟိုကန့်သတ်သီအိုရီတွင် သာမာန်ဖြန့်ဝေမှုသည် ယူဆချက်စမ်းသပ်ခြင်း သို့မဟုတ် ယုံကြည်ချက်ကြားကာလများကဲ့သို့ ကောက်ချက်ချသည့်ကိန်းဂဏန်းတွက်ချက်မှုများကို ခွင့်ပြုပေးသောကြောင့်၊ ဗဟိုကန့်သတ်သီအိုရီတွင် အပလီကေးရှင်းများစွာရှိသည်။ ဥပမာအားဖြင့်၊ ဘဏ္ဍာရေးတွင်၊ ရင်းနှီးမြှုပ်နှံမှုတစ်ခု၏ ပြန်လာမှုနှင့် စွန့်စားရမှုကို ခွဲခြမ်းစိတ်ဖြာရန် ဗဟိုကန့်သတ်သီအိုရီကို အသုံးပြုသည်။

➤ ကြည့်ပါ- သာမာန်ဖြန့်ဖြူးခြင်းဆိုသည်မှာ အဘယ်နည်း။

ဗဟိုကန့်သတ်သီအိုရီ၏ ဥပမာ

ဗဟိုကန့်သတ်သီအိုရီ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို ကျွန်ုပ်တို့မြင်ပြီးသည်နှင့် ၎င်း၏အဓိပ္ပါယ်ကို အပြည့်အဝနားလည်ရန် ဥပမာတစ်ခုကို ကြည့်ကြပါစို့။

ဗဟိုကန့်သတ်သီအိုရီ၏ ဥပမာတစ်ခုသည် အသေကို လှိမ့်ခြင်း ဖြစ်သည်။ ရလဒ်အားလုံးသည် ညီမျှစွာဖြစ်နိုင်သောကြောင့် Die roll သည် သီးခြားတူညီသောဖြန့်ဝေမှု နောက်ဆက်တွဲဖြစ်သည်။ သို့သော် ရလဒ်များစွာ၏ ပေါင်းလဒ်ကို ခွဲဝေခြင်းသည် ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခုသို့ ချဉ်းကပ်သည်။

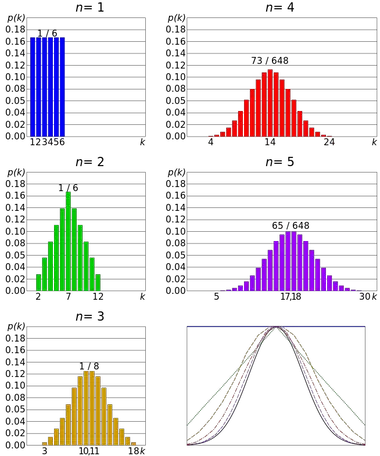
ထို့ကြောင့် ပစ်လွှတ်မှု များလေလေ၊ နည်းလမ်းများ ဖြန့်ဖြူးမှု၏ ပုံသဏ္ဍာန်သည် ပုံမှန် ဖြန့်ဖြူးမှု၏ ဂရပ်နှင့် ဆင်တူနိုင်ခြေ ပိုများလေဖြစ်သည်။

Central Limit Theorem ဖော်မြူလာ

ဗဟိုကန့်သတ်သီအိုရီတွင် လူဦးရေတွင် µ နှင့် စံသွေဖည်မှု σ ရှိပြီး ကျွန်ုပ်တို့သည် လုံလောက်သော အရေအတွက်နမူနာများ (n≥30) ကိုယူပါက၊ နမူနာဆိုလိုသည်မှာ ပျမ်းမျှ µ နှင့် စံသွေဖည်မှု σ ဖြင့် သာမန်ဖြန့်ဖြူးမှုသို့ ခန့်မှန်းနိုင်သည် ။ /√n။

$\displaystyle N\left(\mu,\frac{\sigma}{\sqrt{n}}\right)$

ထို့အပြင် ၊ _{အကယ်၍} X ₁ _သည် အောက်ပါဖော်မြူလာဖြင့် သတ်မှတ်ထားသော ပုံမှန်ဖြန့်ဝေမှုဆီသို့-

$\displaystyle Y=\sum_{i=1}^n X_i \sim N\left(n\cdot \mu,\sigma \cdot \sqrt{n}\right)$

ဗဟိုကန့်သတ်သီအိုရီ၏ လေ့ကျင့်ခန်းကို ဖြေရှင်းခဲ့သည်။

အယူအဆကို အပြည့်အဝ ပေါင်းစပ်နိုင်စေရန်၊ ဤသည်မှာ ဗဟိုကန့်သတ်သီအိုရီ၏ ဖြေရှင်းနိုင်သော လေ့ကျင့်ခန်းတစ်ခုဖြစ်သည်။

ကုမ္ပဏီတစ်ခုသည် အချို့သော အရုပ်အစိတ်အပိုင်းများကို အစားထိုးအသုံးပြုသည့် အစိတ်အပိုင်းများကို ရောင်းချသည်။ အကြွေစေ့တစ်ခုသည် ပျမ်းမျှအလေးချိန် 300 ဂရမ်ရှိပြီး စံသွေဖည်မှု 50 ဂရမ်ရှိသည်။ ဖောက်သည်တစ်ဦးသည် အသုတ် 100 ထည်ကို မှာယူပါက၊ အသုတ်ရှိ အပိုင်းအစများ၏ ပျမ်းမျှအလေးချိန်သည် 305 g ထက် ပိုများနိုင်ခြေ မည်မျှရှိမည်နည်း။ အသုတ် 100 ၏အလေးချိန်သည် 31 ကီလိုဂရမ်ထက်ပိုမိုသောဖြစ်နိုင်ခြေအဘယ်နည်း။

အသုတ်အရွယ်အစားသည် ကြီးမားသောကြောင့် (n=100)၊ ပြဿနာကိုဖြေရှင်းရန် ဗဟိုကန့်သတ်သီအိုရီကို ကျွန်ုပ်တို့အသုံးပြုနိုင်ပါသည်။

ထို့ကြောင့်၊ ဗဟိုကန့်သတ်သီအိုရီဖော်မြူလာကို အသုံးပြု၍ နမူနာနည်းလမ်းများ ဖြန့်ဝေမှုသည် အောက်ပါဘောင်များနှင့်အတူ ပုံမှန်ဖြန့်ဝေမှုတစ်ခုသို့ ခန့်မှန်းနိုင်သည်-

$\displaystyle N\left(\mu,\frac{\sigma}{\sqrt{n}}\right)$

$\mu_{\overline{X}}=\mu=300$

$\sigma_{\overline{X}}=\cfrac{\sigma}{\sqrt{n}}=\cfrac{50}{\sqrt{100}}=5$

$\displaystyle N\left(300,5\right)$

ယခု ကျွန်ုပ်တို့သည် စာရိုက်ခြင်းလုပ်ငန်းစဉ်ကို လုပ်ဆောင်ပြီးနောက် လေ့ကျင့်ခန်းက ကျွန်ုပ်တို့ထံ တောင်းဆိုထားသည့် ဖြစ်နိုင်ခြေကို ရှာဖွေနိုင်မည်ဖြစ်သည်။ ဒါကိုလုပ်ဖို့၊ ဖြန့်ဖြူးမှုကနေ ပျမ်းမျှကို နုတ်ပြီး စံသွေဖည်မှုဖြင့် ပိုင်းခွဲရပါမယ်။

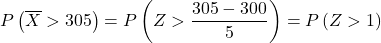$\displaystyle P\left(\overline{X}>305\right)=P\left(Z>\frac{305-300}{5}\right)=P\left(Z>1\right)” title=” Rendered by QuickLaTeX.com” height=” 43″ width=” 381″ style=” vertical-align: -17px;” > ထို့ကြောင့် စာရေးတံရှိ အပိုင်းအစများ၏ ပျမ်းမျှအလေးချိန်သည် 305 g ထက် ပိုများကြောင်း ဖြစ်နိုင်ခြေကို ရှာဖွေရန်၊ <a href=$ ပုံမှန်ဖြန့်ချီရေးဇယား တွင် မည်သည့်တန်ဖိုး Z > 1 နှင့် ကိုက်ညီသည်ကို ကြည့်ရပါမည်။

$\displaystyle P\left(\overline{X}>305\right)=P\left(Z>1\right)=0,1587″ title=” Rendered by QuickLaTeX.com” height=” 22″ width=” 276″ style=” vertical-align: -7px;” > အခြားတစ်ဖက်တွင်၊ ဗဟိုကန့်သတ်သီအိုရီကြောင့် ဒင်္ဂါး 100 တစ်သုတ်သည် ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခုသို့ ချဉ်းကပ်နိုင်သည်ကို ကျွန်ုပ်တို့သိရှိနိုင်သည်၊ အဘယ်ကြောင့်ဆိုသော် ဒင်္ဂါးများအားလုံးသည် တူညီသောဖြန့်ဝေမှုအတိုင်းဖြစ်သည်။ ထို့ကြောင့်၊ အကြွေစေ့ 100 သည် 31 ကီလိုဂရမ်ထက် ပိုအလေးချိန်ရှိနိုင်ခြေကို ဆုံးဖြတ်ရန်၊ ဗဟိုကန့်သတ်သီအိုရီ၏ အခြားဖော်မြူလာကို အသုံးပြုရပါမည်။ <p class=$ $\displaystyle Y=\sum_{i=1}^n X_i \sim N\left(n\cdot \mu,\sigma \cdot \sqrt{n}\right)$

$\displaystyle Y\sim N\left(100\cdot 300,50\cdot \sqrt{100}\right)$

$\displaystyle Y\sim N\left(30000,500\right)$

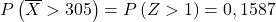
ထို့ကြောင့် ကျွန်ုပ်တို့သည် စာရိုက်ခြင်းလုပ်ငန်းစဉ်ကို ပြန်လည်လုပ်ဆောင်ပြီးနောက် ပြဿနာက ကျွန်ုပ်တို့ကို မေးသည့် ဒုတိယဖြစ်နိုင်ခြေကို ရှာဖွေပါ-

$\displaystyle P\left(Y>31000\right)=P\left(Z>\frac{31000-30000}{500}\right)=P\left(Z>2\right)” title=” Rendered by QuickLaTeX.com” height=” 43″ width=” 430″ style=” vertical-align: -17px;” > နောက်ဆုံးတွင်၊ 100 အပိုင်းအစတစ်ခုသည် ပုံမှန်ဖြန့်ချီရေးဇယားကို အသုံးပြု၍ 31 ကီလိုဂရမ်ထက် အလေးချိန် 31 ကီလိုဂရမ်ထက်ပိုလိမ့်မည်ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်နိုင်သည်- 31000\right)=P\left(Z>2\right)=0,0228″ title=” Rendered by QuickLaTeX.com” height=” 19″ width=” 289″ style=” vertical-align: -5px;” > <div style=$ ➤ 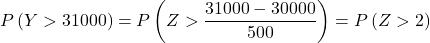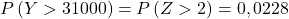အရေအတွက်များသောဥပဒေ ကို ကြည့်ပါ။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။