Central tendency ၏အတိုင်းအတာများ- အဓိပ္ပါယ်ဖွင့်ဆိုချက်များနှင့် ဥပမာများ
ဗဟိုသဘောထားကို အတိုင်းအတာ တစ်ခုသည် ဒေတာအစုတစ်ခု၏ ဗဟိုအမှတ်ကို ကိုယ်စားပြုသည့် တစ်ခုတည်းသောတန်ဖိုးဖြစ်သည်။ ဤတန်ဖိုးကို ဒေတာအစုတစ်ခု၏ “ဗဟိုတည်နေရာ” ဟုလည်း ခေါ်နိုင်သည်။
စာရင်းအင်းများတွင်၊ ဗဟိုသဘောထားကို ဘုံတိုင်းတာမှုသုံးမျိုးရှိသည်။
- ပျှမ်းမျှ
- ပျမ်းမျှ
- ဖက်ရှင်
ဤအစီအမံတစ်ခုစီသည် မတူညီသောနည်းလမ်းများဖြင့် ဒေတာအစုံ၏ဗဟိုတည်နေရာကို ရှာဖွေသည်။ သင်ခွဲခြမ်းစိတ်ဖြာနေသည့် ဒေတာအမျိုးအစားပေါ် မူတည်၍ အခြားနှစ်ခုထက် ဤမက်ထရစ်သုံးခုထဲမှ တစ်ခုကို အသုံးပြုခြင်းသည် ပိုကောင်းပေမည်။
ဤဆောင်းပါးတွင်၊ ဗဟိုသဘောထား၏တိုင်းတာမှုသုံးမျိုးမှ တစ်ခုစီကို တွက်ချက်နည်းအပြင် သင့်ဒေတာအပေါ်အခြေခံ၍ မည်သည့်အတိုင်းအတာကို အသုံးပြုရန် အကောင်းဆုံးဆုံးဖြတ်နည်းကို လေ့လာပါမည်။
ဗဟိုသဘောထားကို တိုင်းတာခြင်းသည် အဘယ်ကြောင့် အသုံးဝင်သနည်း။
ပျမ်းမျှ၊ ပျမ်းမျှ၊ နှင့် မုဒ်တို့ကို တွက်ချက်နည်းကို မကြည့်မီ၊ ဤတိုင်းတာမှုများသည် အဘယ်ကြောင့် အမှန်တကယ် အသုံးဝင်သည်ကို နားလည်ရန် အထောက်အကူဖြစ်စေပါသည်။
အောက်ပါ အဖြစ်အပျက်ကို သုံးသပ်ကြည့်ပါ-
ငယ်ရွယ်သော စုံတွဲတစ်တွဲသည် မြို့သစ်တွင် ၎င်းတို့၏ ပထမဆုံးအိမ်ကို မည်သည့်နေရာတွင် ဝယ်ယူရမည်ကို ဆုံးဖြတ်ရန် ကြိုးစားနေပြီး ၎င်းတို့ အများဆုံးသုံးနိုင်သည်မှာ ဒေါ်လာ ၁၅၀,၀၀၀ ဖြစ်သည်။ မြို့တော်၏ အချို့နေရာများတွင် ဈေးကြီးသောအိမ်များ ၊ အချို့မှာ စျေးပေါသောအိမ်များ ရှိပြီး အချို့မှာ စျေးတန်သော အိမ်များရှိသည်။ ၎င်းတို့၏ ဘတ်ဂျက်နှင့် ကိုက်ညီသော သီးခြားရပ်ကွက်များသို့ ၎င်းတို့၏ ရှာဖွေမှုကို အလွယ်တကူ ကျဉ်းမြောင်းချင်ကြသည်။
အကယ်၍ စုံတွဲများသည် ရပ်ကွက်တစ်ခုစီရှိ မိသားစုအိမ်များ၏စျေးနှုန်းများကိုသာ ကြည့်ရှုပါက၊ မည်သည့်ရပ်ကွက်သည် ၎င်းတို့၏ဘတ်ဂျက်နှင့် အသင့်တော်ဆုံးဖြစ်ကြောင်း ဆုံးဖြတ်ရန် အခက်အခဲရှိနိုင်သည်၊ အကြောင်းမှာ ၎င်းတို့သည် ဤအရာများကို မြင်နိုင်သောကြောင့်ဖြစ်သည်-
ရပ်ကွက်အတွင်း အိမ် စျေးနှုန်း- ဒေါ်လာ ၁၄၀,၀၀၀၊ ၁၉၀,၀၀၀၊ ဒေါ်လာ ၂၆၅,၀၀၀၊ ဒေါ်လာ ၁၁၅,၀၀၀၊ ၂၇၀,၀၀၀၊ ဒေါ်လာ ၂၄၀,၀၀၀၊ ဒေါ်လာ ၂၅၀,၀၀၀၊ ဒေါ်လာ ၁၈၀,၀၀၀၊ ဒေါ်လာ ၁၆၀,၀၀၀၊ ဒေါ်လာ ၂၀၀,၄၀၀,၀၀၀…
ရပ်ကွက် B အိမ်စျေးနှုန်းများ : $140,000, $290,000, $155,000, $165,000, $280,000, $220,000, $155,000, $185,000, $160,000, $200,015,000, $200,015,000, $ ၀ ၀၊…
အိမ်နီးနားချင်း C အိမ်စျေးနှုန်း- $140,000, $130,000, $165,000, $115,000, $170,000, $100,000, $150,000, $180,000, $190,000, $120,010,00, $120,000, $120,000, $120,000, ၀ ၀၊…
သို့သော်၊ ရပ်ကွက်တစ်ခုစီရှိ အိမ်များ၏ ပျမ်းမျှ စျေးနှုန်း (ဥပမာ – ဗဟိုသဘောထားကို တိုင်းတာခြင်း) ကို သိရှိပါက၊ ၎င်းတို့သည် ၎င်းတို့၏ ဘတ်ဂျက်နှင့် ကိုက်ညီသော အိမ်စျေးနှုန်းများကို ပိုမိုလွယ်ကူစွာ သိရှိနိုင်သောကြောင့် ၎င်းတို့၏ ရှာဖွေမှုကို ပိုမိုလျင်မြန်စွာ ပြုပြင်နိုင်သည်-
အနီးနားရှိ အိမ် တစ်အိမ်၏ ပျမ်းမျှစျေးနှုန်း A- $220,000
ရပ်ကွက် B တွင် အိမ်တစ်လုံး၏ ပျမ်းမျှစျေးနှုန်းမှာ $190,000 ဖြစ်သည်။
အနီးနားရှိ အိမ်တစ်အိမ်၏ပျမ်းမျှစျေးနှုန်း C : $140,000
ရပ်ကွက်တစ်ခုစီရှိ ပျမ်းမျှအိမ်စျေးနှုန်းကို သိရှိခြင်းဖြင့်၊ Neighborhood C သည် ၎င်းတို့၏ဘတ်ဂျက်အတွင်း အိမ်အများဆုံးရနိုင်ဖွယ်ရှိကြောင်း လျင်မြန်စွာတွေ့မြင်နိုင်သည်။
၎င်းသည် ဗဟိုသဘောထားကို အတိုင်းအတာတစ်ခုအထိ အသုံးပြုခြင်း၏ အကျိုးကျေးဇူးဖြစ်သည်- ၎င်းသည် ဒေတာတန်ဖိုးများ ယေဘုယျအားဖြင့် မည်သည့်နေရာတွင်ရှိကြောင်း ဖော်ပြလေ့ရှိသည့် ဒေတာအစုတစ်ခု၏ ဗဟိုတန်ဖိုးကို နားလည်ရန် ကူညီပေးသည်။ ဤဥပမာတွင်၊ ရပ်ကွက်တစ်ခုစီရှိ အိမ်တစ်အိမ်၏ပုံမှန်စျေးနှုန်းကို လူငယ်မောင်နှံနှစ်ဦး နားလည်စေရန် ကူညီပေးသည်။
Takeaway- ဒေတာအစုတစ်ခု၏ “ ဗဟို” ကိုဖော်ပြသည့် တစ်ခုတည်းသောတန်ဖိုးကို ကျွန်ုပ်တို့အား ပေးဆောင်သောကြောင့် ဗဟိုသဘောထား၏အတိုင်းအတာသည် အသုံးဝင်ပါသည်။ ၎င်းသည် data set အတွင်းရှိ တစ်ဦးချင်းတန်ဖိုးအားလုံးကို ကြည့်ရုံထက် ဒေတာအစုံကို ပိုမိုမြန်ဆန်စွာ နားလည်နိုင်ရန် ကူညီပေးပါသည်။
ဆိုလိုတာ
ဗဟိုသဘောထားကို တိုင်းတာရာတွင် အသုံးအများဆုံးမှာ ပျမ်းမျှ ဖြစ်သည်။ ဒေတာအစုတစ်ခု၏ ပျမ်းမျှအား တွက်ချက်ရန်၊ တစ်ဦးချင်းတန်ဖိုးများအားလုံးကို ပေါင်းထည့်ကာ စုစုပေါင်းတန်ဖိုးအရေအတွက်ဖြင့် ပိုင်းခြားပါ။
ပျမ်းမျှ = (တန်ဖိုးအားလုံး၏ပေါင်းလဒ်) / (စုစုပေါင်းတန်ဖိုးများ)
ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့တွင် တစ်ရာသီအတွင်း တစ်သင်းတည်းရှိ ဘေ့စ်ဘောကစားသမား 10 ဦးမှ အိမ်ပြန်ပြေးခြင်းကို ပြသသည့် အောက်ပါဒေတာအစုံရှိသည်ဆိုပါစို့။
| ဘာညာ | #၁ | #၂ | #၃ | #၄ | #၅ | #၆ | #၇ | #၈ | #၉ | #တကျိပ် |
|---|---|---|---|---|---|---|---|---|---|---|
| အိမ်ပြန်ပြေးတယ်။ | ၈ | ၁၅ | ၂၂ | ၂၁ | ၁၂ | ၉ | ၁၁ | ၂၇ | ၁၄ | ၁၃ |
ကစားသမားတစ်ဦးလျှင် ပျမ်းမျှ အိမ်ကွင်းပြေးနှုန်းကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။
ပျမ်းမျှ = (8+15+22+21+12+9+11+27+14+13) / 10 = 15.2 ဆားကစ်များ ။
မီဒီယံ
ပျမ်းမျှ သည် ဒေတာအတွဲတစ်ခု၏ အလယ်တန်ဖိုးဖြစ်သည်။ အသေးဆုံးမှ အကြီးဆုံးမှ အကြီးဆုံးအထိ ဒေတာသတ်မှတ်မှုတွင် တစ်ဦးချင်းတန်ဖိုးများအားလုံးကို စီစဥ်ပြီး ပျမ်းမျှတန်ဖိုးကို ရှာဖွေခြင်းဖြင့် ပျမ်းမျှအား ရှာဖွေနိုင်သည်။ ကိန်းဂဏန်းများ၏ ထူးဆန်းသောတန်ဖိုးများရှိပါက ပျမ်းမျှသည် အလယ်တန်ဖိုးဖြစ်သည်။ တူညီသောတန်ဖိုးများရှိပါက ပျမ်းမျှသည် အလယ်တန်ဖိုးနှစ်ခု၏ ပျမ်းမျှဖြစ်သည်။
ဥပမာအားဖြင့်၊ ယခင်နမူနာတွင် ဘေ့စ်ဘောကစားသမား 10 ဦးမှ ထိမှန်သော ပျမ်းမျှအိမ်ပြေးအရေအတွက်ကို ရှာဖွေရန်၊ ကျွန်ုပ်တို့သည် ကစားသမားများကို အိမ်ကွင်းပြေးပွဲအရေအတွက်၏ ကြီးစဉ်ငယ်လိုက် အဆင့်သတ်မှတ်နိုင်သည်-
| ဘာညာ | #၁ | #၆ | #၇ | #၅ | #တကျိပ် | #၉ | #၂ | #၄ | #၃ | #၈ |
|---|---|---|---|---|---|---|---|---|---|---|
| အိမ်ပြန်ပြေးတယ်။ | ၈ | ၉ | ၁၁ | ၁၂ | ၁၃ | ၁၄ | ၁၅ | ၂၁ | ၂၂ | ၂၇ |
ကျွန်ုပ်တို့တွင် တူညီသောတန်ဖိုးများရှိသည်ဖြစ်သောကြောင့် ပျမ်းမျှသည် အလယ်တန်းတန်ဖိုးနှစ်ခု၏ ပျမ်းမျှဖြစ်သည်- 13.5 ဖြစ်သည်။
ယင်းအစား၊ ကျွန်ုပ်တို့တွင် ကစားသမား ကိုးဦးရှိလျှင် စဉ်းစားပါ။
| ဘာညာ | #၁ | #၆ | #၇ | #၅ | #၉ | #၂ | #၄ | #၃ | #၈ |
|---|---|---|---|---|---|---|---|---|---|
| အိမ်ပြန်ပြေးတယ်။ | ၈ | ၉ | ၁၁ | ၁၂ | ၁၄ | ၁၅ | ၂၁ | ၂၂ | ၂၇ |
ဤကိစ္စတွင်၊ ကျွန်ုပ်တို့တွင် ကိန်းဂဏန်းတန်ဖိုးများ ရှိနေသောကြောင့်၊ ပျမ်းမျှသည် ရိုးရိုးအလယ်တန်ဖိုးဖြစ်သည်- 14 ။
ဖက်ရှင်
မုဒ် သည် ဒေတာအတွဲတစ်ခုတွင် အများဆုံးတွေ့ရသည့် တန်ဖိုးဖြစ်သည်။ ဒေတာအစုံတွင် မုဒ်များမရှိပါ (တန်ဖိုးများ ထပ်ကျော့ပါက) မုဒ်တစ်ခု သို့မဟုတ် မုဒ်များစွာရှိနိုင်သည်။
ဥပမာအားဖြင့်၊ အောက်ပါဒေတာအတွဲတွင် မုဒ်မရှိပါ-
| ဘာညာ | #၁ | #၂ | #၃ | #၄ | #၅ | #၆ | #၇ | #၈ | #၉ | #တကျိပ် |
|---|---|---|---|---|---|---|---|---|---|---|
| အိမ်ပြန်ပြေးတယ်။ | ၈ | ၉ | ၁၁ | ၁၂ | ၁၃ | ၁၄ | ၁၅ | ၂၁ | ၂၂ | ၂၇ |
အောက်ပါဒေတာအတွဲတွင် မုဒ်တစ်ခုပါရှိသည်- 15 . ဤသည်မှာ မကြာခဏပေါ်လာသော တန်ဖိုးဖြစ်သည်။
| ဘာညာ | #၁ | #၂ | #၃ | #၄ | #၅ | #၆ | #၇ | #၈ | #၉ | #တကျိပ် |
|---|---|---|---|---|---|---|---|---|---|---|
| အိမ်ပြန်ပြေးတယ်။ | ၈ | ၉ | ၁၁ | ၁၂ | ၁၃ | ၁၅ | ၁၅ | ၂၁ | ၂၂ | ၂၇ |
အောက်ပါဒေတာအတွဲတွင် 8၊ 15၊ 19 မုဒ်သုံးမျိုးရှိသည်။ ဤရွေ့ကားတန်ဖိုးများမကြာခဏပေါ်လာသည်။
| ဘာညာ | #၁ | #၂ | #၃ | #၄ | #၅ | #၆ | #၇ | #၈ | #၉ | #တကျိပ် |
|---|---|---|---|---|---|---|---|---|---|---|
| အိမ်ပြန်ပြေးတယ်။ | ၈ | ၈ | ၁၁ | ၁၂ | ၁၅ | ၁၅ | ၁၇ | ၁၉ | ၁၉ | ၂၇ |
မုဒ်သည် အမျိုးအစားအလိုက် ကိန်းဂဏန်း အချက်အလက်များနှင့် လုပ်ဆောင်သည့်အခါ အထူးအသုံးဝင်သော အတိုင်းအတာတစ်ခု ဖြစ်နိုင်သည်၊ အကြောင်းမှာ ၎င်းသည် မည်သည့်အမျိုးအစားတွင် အများဆုံးပေါ်လာသည်ကို ကျွန်ုပ်တို့ကိုပြောပြသောကြောင့်ဖြစ်သည်။ ဥပမာအားဖြင့်၊ လူတို့၏အနှစ်သက်ဆုံးအရောင်နှင့်ပတ်သက်သည့် စစ်တမ်းရလဒ်များကိုပြသသည့် အောက်ပါဘားဇယားကို သုံးသပ်ကြည့်ပါ-
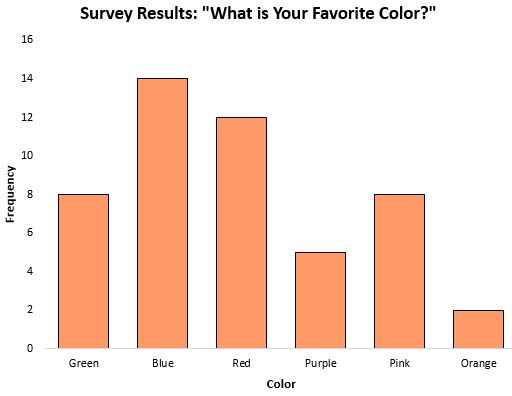
မုဒ် သို့မဟုတ် မကြာခဏဖြစ်ပေါ်သည့် တုံ့ပြန်မှုသည် အပြာရောင်ဖြစ်သည်။
ဒေတာသည် အမျိုးအစားခွဲခြားသည့်အခြေအနေများတွင် (အထက်ဖော်ပြပါပုံကဲ့သို့) ပျမ်းမျှ သို့မဟုတ် ဆိုလိုရင်းကို တွက်ချက်ရန်ပင်မဖြစ်နိုင်သောကြောင့် မုဒ်သည် ကျွန်ုပ်တို့သုံးနိုင်သည့်တစ်ခုတည်းသော ဗဟိုသဘောထားကို တိုင်းတာခြင်းဖြစ်သည်။
အထက်နမူနာတွင် ဘေ့စ်ဘောကစားသမားများနှင့် အထက်တွင်တွေ့ခဲ့သည့်အတိုင်း ဂဏန်းဒေတာအတွက် မုဒ်ကိုလည်း အသုံးပြုနိုင်သည်။ သို့သော်၊ “ ဤဒေတာအတွဲအတွက် ပုံမှန်တန်ဖိုးက ဘာလဲ” မေးခွန်းကိုဖြေဆိုရန်အတွက် မုဒ်သည် အသုံးနည်းပါသည်။ »
ဥပမာအားဖြင့်၊ ဤအသင်းရှိ ဘေ့စ်ဘောကစားသမားမှ ထိမှန်သည့် အိမ်ကွင်းအရေအတွက်ကို ကျွန်ုပ်တို့ သိလိုသည်ဆိုပါစို့-
| ဘာညာ | #၁ | #၂ | #၃ | #၄ | #၅ | #၆ | #၇ | #၈ | #၉ | #တကျိပ် |
|---|---|---|---|---|---|---|---|---|---|---|
| အိမ်ပြန်ပြေးတယ်။ | ၈ | ၈ | ၁၁ | ၁၂ | ၁၅ | ၁၅ | ၁၇ | ၁၉ | ၁၉ | ၂၇ |
ဤဒေတာအတွဲအတွက် မုဒ်မှာ 8၊ 15 နှင့် 19 ဖြစ်သောကြောင့် ၎င်းတို့သည် မကြာခဏတန်ဖိုးများဖြစ်သည်။ သို့သော်၊ ၎င်းတို့သည် အသင်းရှိ ကစားသမားတစ်ဦးမှ ထိမှန်သော ပုံမှန်အိမ်ကွင်းအရေအတွက်ကို နားလည်ရန် အထောက်အကူမဖြစ်ပေ။ ဤကိစ္စတွင် ဗဟိုသဘောထား၏ ပိုကောင်းသည့်အတိုင်းအတာသည် ပျမ်းမျှ (15) သို့မဟုတ် ပျမ်းမျှ (15) ဖြစ်နိုင်သည်။
မုဒ်သည် ကျန်တန်ဖိုးများနှင့် ဝေးကွာသော ဂဏန်းတစ်ခုဖြစ်သောကြောင့် ဗဟိုသဘောထား၏ ညံ့ဖျင်းသော အတိုင်းအတာတစ်ခုလည်းဖြစ်သည်။ ဥပမာအားဖြင့်၊ အောက်ပါဒေတာအစုံ၏မုဒ်သည် 30 ဖြစ်သည်၊ သို့သော် ၎င်းသည် အသင်းတွင်ကစားသမားတစ်ဦးစီ၏ “ ပုံမှန်” အိမ်ပြေးအရေအတွက်ကို အမှန်တကယ်ကိုယ်စားပြုခြင်းမရှိပါ။
| ဘာညာ | #၁ | #၂ | #၃ | #၄ | #၅ | #၆ | #၇ | #၈ | #၉ | #တကျိပ် |
|---|---|---|---|---|---|---|---|---|---|---|
| အိမ်ပြန်ပြေးတယ်။ | ၅ | ၆ | ၇ | တကျိပ် | ၁၁ | ၁၂ | ၁၃ | ၁၅ | ၃၀ | ၃၀ |
တဖန်၊ ပျမ်းမျှ သို့မဟုတ် အလယ်အလတ်သည် ဤဒေတာအစု၏ ဗဟိုတည်နေရာကို ဖော်ပြခြင်းအတွက် ပိုမိုကောင်းမွန်သောအလုပ်ဖြစ်လိမ့်မည်။
Mean၊ Median နှင့် Mode ကို ဘယ်အချိန်မှာ သုံးမလဲ။
ပျမ်းမျှ၊ အလယ်အလတ်နှင့် မုဒ်တို့သည် ဒေတာသတ်မှတ်မှုတစ်ခု၏ ဗဟိုတည်နေရာ သို့မဟုတ် “ ပုံမှန်တန်ဖိုး” ကို တိုင်းတာကြသည်ကို ကျွန်ုပ်တို့တွေ့မြင်ခဲ့ရသည်-
ပျမ်းမျှ- ဒေတာအတွဲတစ်ခုရှိ ပျမ်းမျှတန်ဖိုးကို ရှာပါ။
မီဒီယံ- ဒေတာအတွဲတစ်ခုတွင် ပျမ်းမျှတန်ဖိုးကို ရှာပါ။
မုဒ်- ဒေတာအတွဲတစ်ခုတွင် အတွေ့ရအများဆုံးတန်ဖိုးကို ရှာပါ။
ဤသည်မှာ အချို့သော ဗဟိုသဘောထား၏ တိုင်းတာမှုမှာ အခြားအရာများထက် ပိုမိုအသုံးပြုရန် ပိုမိုကောင်းမွန်သည့် အခြေအနေများဖြစ်သည်။
ပျမ်းမျှကို ဘယ်အချိန်မှာ သုံးမလဲ။
ဒေတာဖြန့်ဝေမှုသည် မျှမျှတတ အချိုးကျပြီး အစွန်းအထင်းမရှိသည့်အခါ ပျမ်းမျှအား အသုံးပြုခြင်းသည် အကောင်းဆုံးဖြစ်သည်။
ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့တွင် မြို့တစ်မြို့ရှိ လူတစ်ဦးချင်းစီ၏ လစာများကို ဖော်ပြသော အောက်ပါ ဖြန့်ဖြူးမှုတစ်ခုရှိသည် ဆိုပါစို့။

ဤဖြန့်ဝေမှုသည် မျှမျှတတ အချိုးကျသောကြောင့် (ဆိုလိုသည်မှာ ၎င်းကို တစ်ဝက်စီခွဲပါက၊ တစ်ဝက်စီသည် အကြမ်းဖျင်းတူညီမည်) နှင့် အစွန်းအထင်းများမရှိပါ (ဆိုလိုသည်မှာ (ဆိုလိုသည်မှာ လစာအလွန်မြင့်မားခြင်းမရှိပါ)၊ ပျမ်းမျှသည် ဤဒေတာအစုကို ဖော်ပြခြင်းအတွက် ကောင်းမွန်သောအလုပ်ဖြစ်လိမ့်မည်။
ပျမ်းမျှအားဖြင့် $63,000 သည် ဖြန့်ဖြူးမှု၏အလယ်တွင် အကြမ်းဖျင်းဖြစ်သည်-

အလယ်အလတ်ကို ဘယ်အချိန်မှာ သုံးမလဲ။
ဒေတာဖြန့်ဝေမှု လွဲသွားသည့်အခါ သို့မဟုတ် အစွန်းအထင်းများရှိသည့်အခါ အလယ်အလတ်ကို အသုံးပြုခြင်းသည် အကောင်းဆုံးဖြစ်သည်။
ဘက်လိုက်သောဒေတာ-
ဖြန့်ဝေမှု လွဲသွားသောအခါ အလယ်အလတ်သည် ဗဟိုတည်နေရာကို ဖမ်းယူနိုင်ဆဲဖြစ်သည်။ ဥပမာအားဖြင့်၊ အချို့သောမြို့တစ်ခုရှိ လူတစ်ဦးချင်းစီ၏ လစာများ ခွဲဝေမှုကို ထည့်သွင်းစဉ်းစားပါ-

ပျမ်းမျှသည် လူတစ်ဦးချင်းစီ၏ ပျမ်းမျှလစာထက် သာလွန်ကောင်းမွန်သည်ကို ထင်ဟပ်စေသည်။ အဘယ်ကြောင့်ဆိုသော် ဖြန့်ဖြူးမှုတစ်ခု၏အမြီးရှိ ကြီးမားသောတန်ဖိုးများသည် ပျမ်းမျှအား ဗဟိုမှဝေးကွာပြီး အမြီးရှည်ဆီသို့ ရွေ့သွားတတ်သောကြောင့်ဖြစ်သည်။
ဤဥပမာတွင်၊ သာမန်လူတစ်ဦးတစ်ယောက်သည် ဤမြို့၌ တစ်နှစ်လျှင် $47,000 ဝန်းကျင်ဝင်ငွေရှိကြောင်း၊ ပျမ်းမျှအားဖြင့် သာမန်လူတစ်ဦးတစ်ယောက်သည် တစ်နှစ်လျှင် $32,000 ဝန်းကျင်သာရရှိသည်၊ ၎င်းသည် သာမန်လူတစ်ဦးချင်းစီ၏ ပို၍ကိုယ်စားပြုသည်ဟု ပျမ်းမျှအားဖြင့်ပြောပြသည်။
အစွန်းထွက်များ-
ဒေတာတွင် အစွန်းအထင်းများရှိနေသောအခါ အလယ်အလတ်သည် ဖြန့်ဖြူးမှု၏ဗဟိုတည်နေရာကို ပိုမိုကောင်းမွန်စွာဖမ်းယူနိုင်စေရန် ကူညီပေးပါသည်။ ဥပမာအားဖြင့်၊ အချို့သောလမ်းပေါ်ရှိ အိမ်များ၏စတုရန်းပုံများကိုပြသသည့် အောက်ပါဂရပ်ကို သုံးသပ်ကြည့်ပါ-

ပျမ်းမျှအား အလယ်အလတ်မရှိသော်လည်း အလွန်ကြီးမားသောအိမ်အနည်းငယ်မှ ကြီးကြီးမားမားလွှမ်းမိုးထားသည်။ ထို့ကြောင့်၊ အလယ်အလတ်သည် ထိုလမ်းပေါ်ရှိ အိမ်တစ်အိမ်၏ “ ပုံမှန်” စတုရန်းပုံများကို ပျမ်းမျှထက် သာလွန်ကောင်းမွန်သည့်အလုပ်ကို လုပ်နိုင်သည် ။
မုဒ်ကို ဘယ်အချိန်မှာ သုံးမလဲ။
သင်သည် အမျိုးအစားအလိုက် ဒေတာများဖြင့် လုပ်ဆောင်နေပြီး မည်သည့်အမျိုးအစားတွင် အများဆုံးပေါ်လာသည်ကို သိလိုသောအခါတွင် ဤမုဒ်ကို အကောင်းဆုံး အသုံးပြုပါသည်။ ဤသည်မှာ ဥပမာအချို့ဖြစ်သည်။
- သင်သည် လူတို့၏အနှစ်သက်ဆုံးအရောင်များကို စစ်တမ်းကောက်ယူနေပြီး တုံ့ပြန်မှုများတွင် ဘယ်အရောင်က အများဆုံးတွေ့ရသည်ကို သိလိုပါသည်။
- သင်သည် ဝဘ်ဆိုဒ်ဒီဇိုင်းအတွက် ရွေးချယ်မှု သုံးခုထဲမှ လူများ၏ နှစ်သက်မှုကို စစ်တမ်းတစ်ခု ပြုလုပ်နေပြီး မည်သည့် ဒီဇိုင်းကို လူများ အနှစ်သက်ဆုံးဖြစ်သည်ကို သိလိုပါသည်။
အစောပိုင်းတွင် ဖော်ပြခဲ့သည့်အတိုင်း၊ သင်သည် အမျိုးအစားအလိုက် ဒေတာဖြင့် လုပ်ဆောင်နေပါက၊ အလယ်ဗဟိုသဘောထားကို တစ်ခုတည်းသော တိုင်းတာမှုအဖြစ် မုဒ်မှ ထွက်သွားသည့် ပျမ်းမျှ သို့မဟုတ် ဆိုလိုရင်းကို တွက်ချက်ရန်ပင် မဖြစ်နိုင်ပါ။
ယေဘုယျအားဖြင့်၊ သင်သည် အိမ်များ၏ စတုရန်းပုံ၊ အိမ်ပြေးအရေအတွက်၊ ကစားသမားတစ်ဦးစီ၊ တစ်ဦးချင်းအလိုက် လစာစသည်ဖြင့် ကိန်းဂဏာန်းအချက်အလက်များကို လုပ်ဆောင်နေပါက၊ “ ပုံမှန်” တန်ဖိုးကို ဖော်ပြရန် ပျမ်းမျှ သို့မဟုတ် ပျမ်းမျှကို အသုံးပြုခြင်းသည် များသောအားဖြင့် အကောင်းဆုံးဖြစ်သည်။ ဒေတာအစုံ။
မှတ်ချက်- ဒေတာအစုံကို ပုံမှန်အတိုင်း ဖြန့်ဝေပါက ပျမ်းမျှ၊ အလယ်အလတ်နှင့် မုဒ်အားလုံးသည် တူညီသောတန်ဖိုးရှိကြောင်း သတိပြုရန် အရေးကြီးပါသည်။