ဘက်စုံဖြန့်ဖြူးခြင်းဆိုသည်မှာ အဘယ်နည်း။

ဘက်စုံဖြန့်ဝေမှု ဆိုသည်မှာ မုဒ်နှစ်ခု သို့မဟုတ် ထို့ထက်ပိုသော မုဒ်နှစ်ခုပါရှိသော ဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။

ဘက်စုံဖြန့်ဝေမှုကို မြင်သာစေရန် ဟီစတိုဂရမ်တစ်ခုကို ဖန်တီးပါက၊ ၎င်းတွင် အထွတ်အထိပ်များစွာရှိကြောင်း သင်သတိပြုမိလိမ့်မည်-

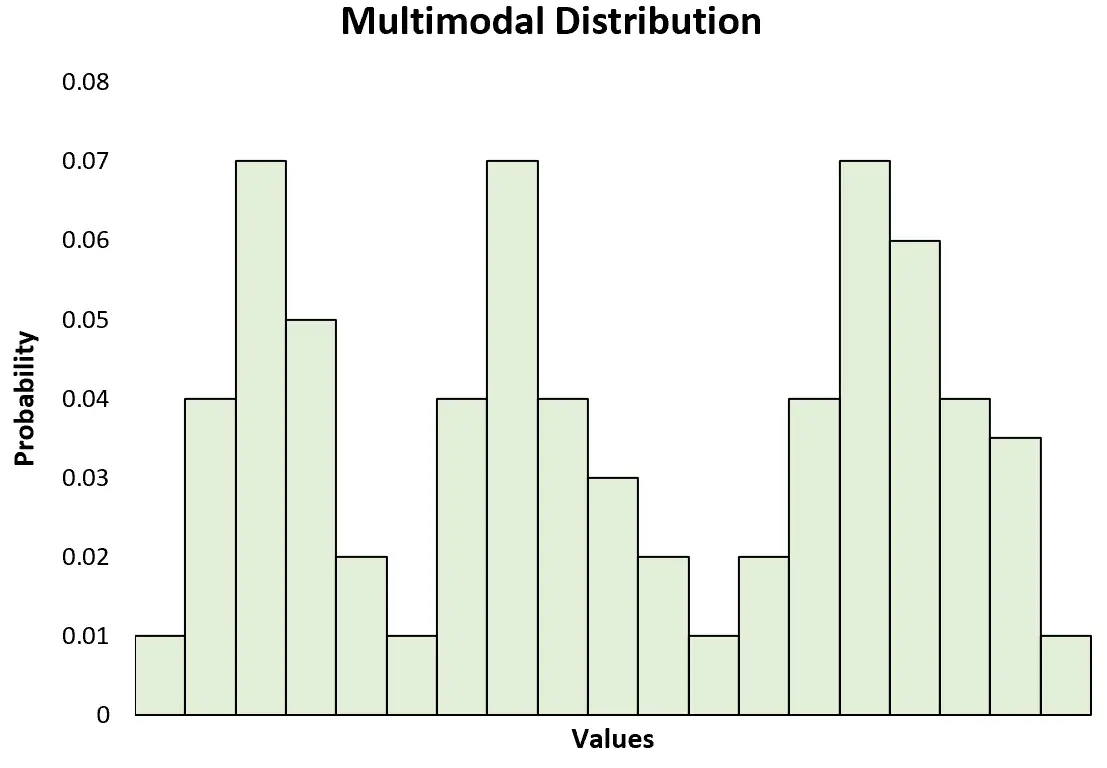
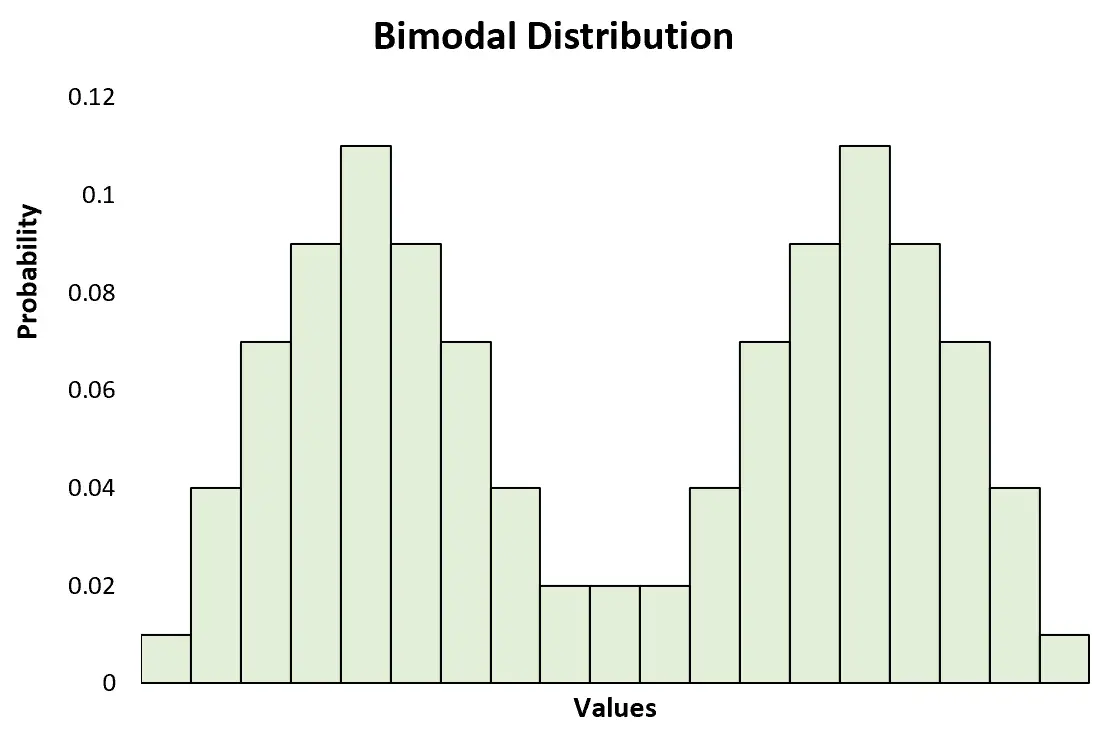
ဖြန့်ဖြူးမှုတစ်ခုတွင် အထွတ်အထိပ်နှစ်ခုတိတိရှိလျှင် ၎င်းကို ဘက်စုံဖြန့်ဝေမှု အမျိုးအစားတစ်ခုဖြစ်သည့် bimodal distribution ဟု သတ်မှတ်သည်။

၎င်းသည် အထွတ်အထိပ်တစ်ခုသာရှိသည့် စံမညီသော ဖြန့်ဖြူးမှုနှင့် ဆန့်ကျင်ဘက်ဖြစ်သည်။

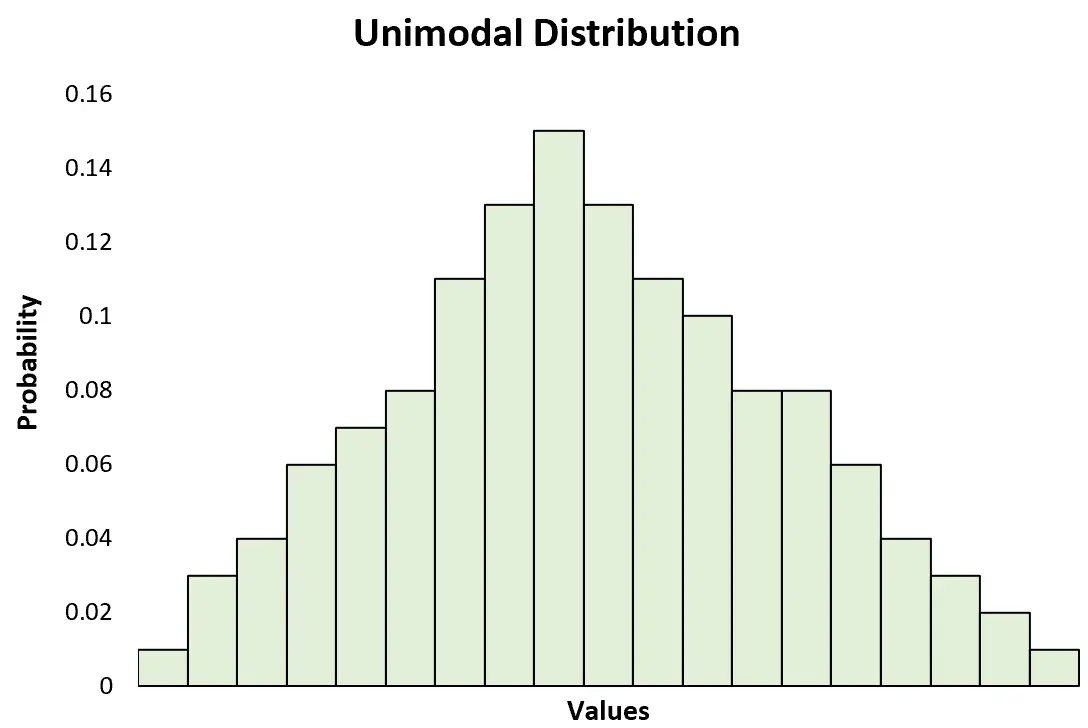
သာမာန်ဖြန့်ဝေမှုကဲ့သို့ သာမာန်ဖြ န့်ဖြူးမှုများကဲ့သို့ တူညီသောဖြန့်ဝေမှုများကို စာရင်းဇယားများတွင် အကြောင်းအရာများကို ရှင်းပြရန် အများဆုံးအသုံးပြုသော်လည်း၊ ဘက်စုံဖြန့်ဝေမှုများကို အမှန်တကယ် လက်တွေ့တွင် မကြာခဏတွေ့ရသောကြောင့် ၎င်းတို့အား အသိအမှတ်ပြုရန်နှင့် ခွဲခြမ်းစိတ်ဖြာနည်းကို သိရှိရန် အသုံးဝင်ပါသည်။

ဘက်စုံဖြန့်ဝေမှု နမူနာများ

ဤသည်မှာ ဘက်စုံဖြန့်ဖြူးခြင်း၏ ဥပမာအချို့ဖြစ်သည်။

ဥပမာ 1- စာမေးပွဲရလဒ်များ ဖြန့်ဝေခြင်း။

ပါမောက္ခတစ်ယောက်က သူ့အတန်းကို စာမေးပွဲဖြေတယ်ဆိုပါစို့။ တချို့ကျောင်းသားတွေက စာမသင်ကြဘူး။ ပရော်ဖက်ဆာက စာမေးပွဲရမှတ်များ၏ ဟီစတိုဂရမ်ကို ဖန်တီးသောအခါ၊ ၎င်းသည် စာမကျက်သော ကျောင်းသားများအတွက် အနိမ့်ဆုံးရမှတ်များဝန်းကျင် အထွတ်အထိပ်ဖြင့် ဘက်စုံဖြန့်ဝေမှုကို လိုက်နာပြီး လေ့လာမှုပြုလုပ်သော ကျောင်းသားများအတွက် မြင့်မားသောရမှတ်များအနီးတွင် အခြားသော အထွတ်အထိပ်တစ်ခုဖြစ်သည်။

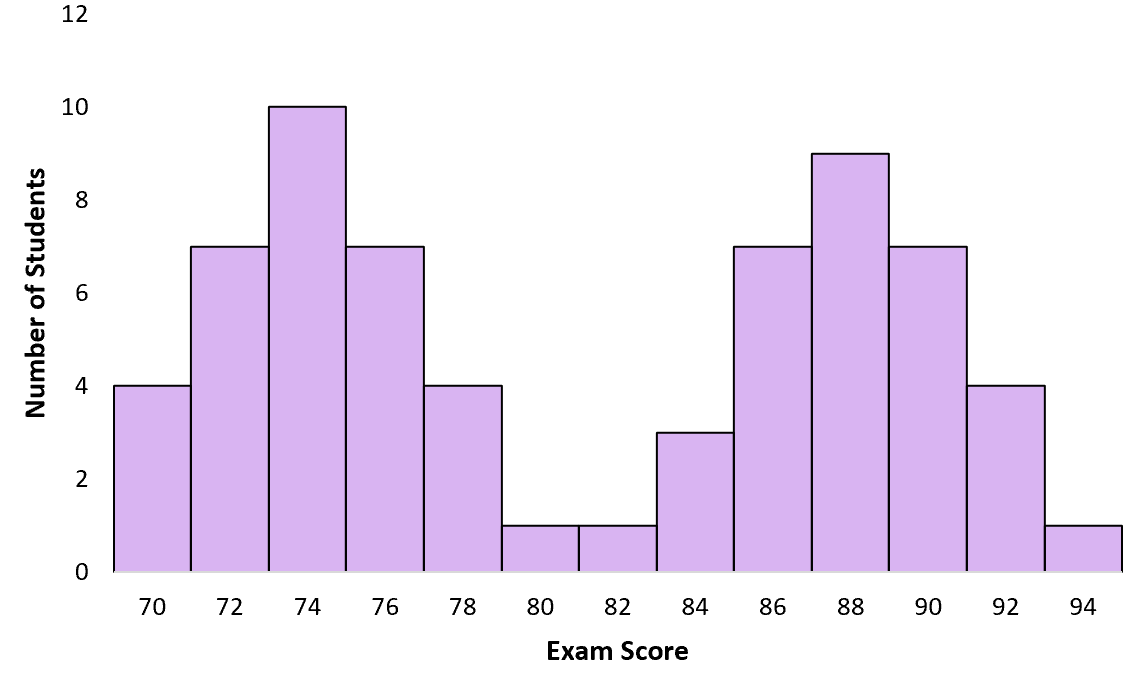
ဥပမာ 2- မတူညီသော အပင်မျိုးစိတ်များ၏ အမြင့်

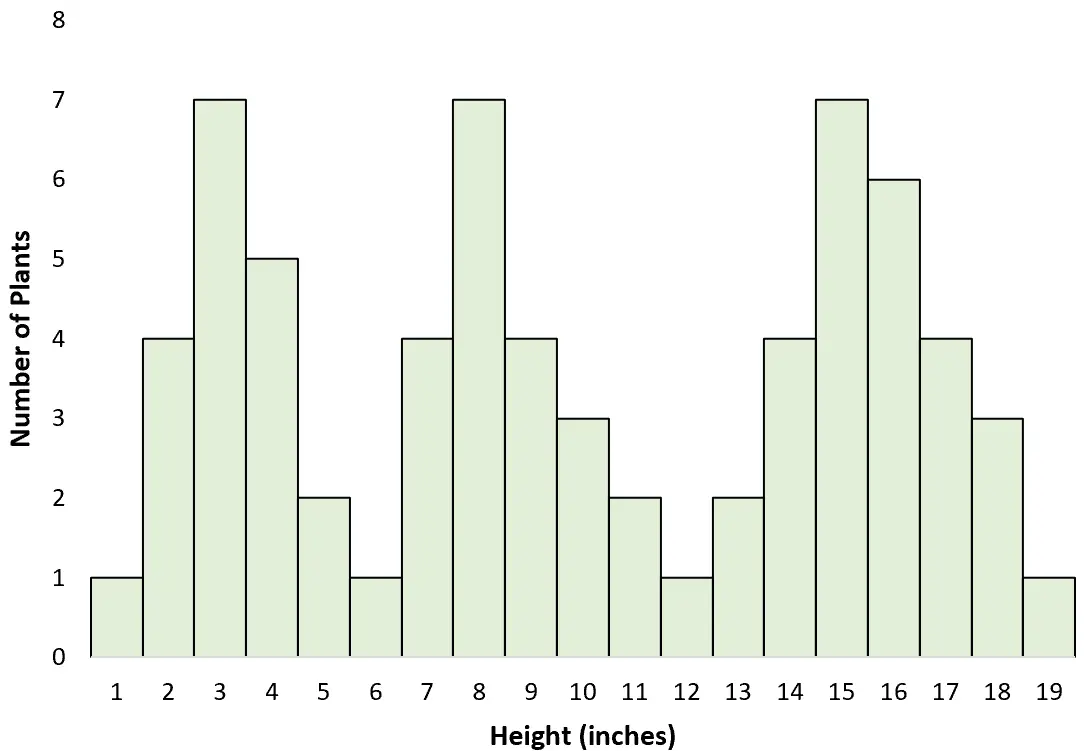
သိပ္ပံပညာရှင်တစ်ဦးသည် ကွင်းပြင်တစ်ဝိုက်တွင် လမ်းလျှောက်ပြီး မတူညီသောအပင်များ၏ အမြင့်ကို တိုင်းတာသည်ဆိုပါစို့။ ၎င်းကို သတိမထားမိဘဲ အမျိုးအစားသုံးမျိုး၏ အရွယ်အစားကို တိုင်းတာသည်- တစ်မျိုးသည် အလွန်ကြီးသည်၊ နောက်တစ်မျိုးမှာ အလတ်စားနှင့် နောက်တစ်မျိုးမှာ အလွန်သေးငယ်သည်။

အမြင့်ဖြန့်ချီမှုကို မြင်သာစေရန် ဟစ်စတိုဂရမ်တစ်ခုကို ဖန်တီးသောအခါ၊ ၎င်းသည် ဘက်စုံပုံစံဖြစ်ကြောင်း သူမတွေ့ရှိခဲ့သည်- တောင်ထိပ်တစ်ခုစီသည် မတူညီသောမျိုးစိတ်သုံးမျိုး၏ အသုံးအများဆုံးအမြင့်ကို ကိုယ်စားပြုသည်။

ဥပမာ 3- ဖောက်သည်များကို ဖြန့်ဝေခြင်း။

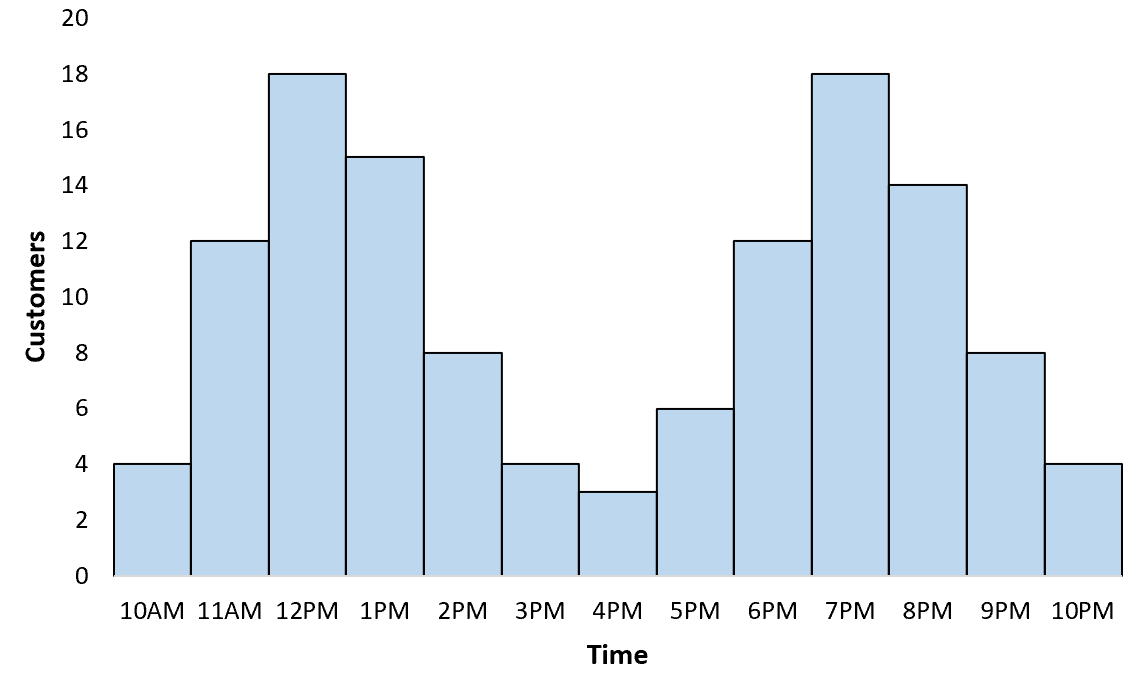
စားသောက်ဆိုင်ပိုင်ရှင်သည် တစ်နာရီလျှင် လာရောက်လည်ပတ်သူအရေအတွက်ကို ခြေရာခံသည်။ ဖောက်သည်များ၏ ဖြန့်ဖြူးမှုကို မြင်သာစေရန် histogram တစ်ခုကို ဖန်တီးသောအခါ၊ ဖြန့်ဖြူးမှုသည် ဘက်စုံသုံးကြောင်း တွေ့ရသည်- နေ့လယ်စာစားချိန်အတွင်း အထွတ်အထိပ်နှင့် ညစာစားချိန်အတွင်း အခြားအထွတ်အထိပ်ရှိသည်။

Multimodal Distribution တွေရဲ့ အကြောင်းရင်းတွေက ဘာတွေလဲ။

အများအားဖြင့် ဘက်စုံဖြန့်ဝေမှုများ၏ အရင်းခံအကြောင်းရင်း နှစ်ခုအနက်မှ တစ်ခု ရှိသည်-

1. အဖွဲ့များစွာကို တစုတစည်းတည်း ဖွဲ့ထားသည်။

သင်မသိလိုက်ဘဲ အုပ်စုများစွာအတွက် ဒေတာကို စုဆောင်းသည့်အခါ Multimodal distributions များ ဖြစ်ပေါ်နိုင်သည်။

ဥပမာအားဖြင့်၊ သိပ္ပံပညာရှင်တစ်ဦးသည် တူညီသောနယ်ပယ်တွင်ရှိသော မတူညီသောအပင်မျိုးစိတ်သုံးမျိုး၏ အမြင့်ကို မသိလိုက်ဘဲ တိုင်းတာပါက၊ အပင်အားလုံး၏ ဖြန့်ကျက်မှုသည် တူညီသော histogram ပေါ်တွင် ထားရှိသောအခါတွင် ဘက်စုံသုံးပုံပေါ်မည်ဖြစ်သည်။

၂။ အရင်းခံဖြစ်စဉ်တစ်ခုရှိတယ်။

အချို့သော နောက်ခံဖြစ်စဉ်များကြောင့် ဘက်စုံဖြန့်ဝေမှုများလည်း ဖြစ်ပွားနိုင်သည်။

ဥပမာအားဖြင့်၊ စားသောက်ဆိုင်သို့ တစ်နာရီလျှင် တစ်နာရီလျှင် လာရောက်သော ဖောက်သည် အရေအတွက်သည် စားသောက်ဆိုင်များတွင် ကွဲပြားသည့်အချိန် နှစ်ကြိမ်- နေ့လည်စာနှင့် ညစာ စားသုံးလေ့ရှိသောကြောင့် ဘက်စုံဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်သည်။ ဤအခြေခံလူ့အပြုအမူသည် ဘက်စုံဖြန့်ဖြူးခြင်း၏ မူလအစဖြစ်သည်။

ဘက်စုံဖြန့်ဝေမှုများကို ခွဲခြမ်းစိတ်ဖြာနည်း

ဖြန့်ဖြူးမှု၏ “ ဗဟို” သည် အဘယ်မှာရှိသည်ကို ကျွန်ုပ်တို့အား အကြံဥာဏ်ပေးသောကြောင့် ပျမ်းမျှ သို့မဟုတ် အလယ်အလတ်ကို အသုံးပြု၍ ဖြန့်ဖြူးမှုများကို မကြာခဏဖော်ပြပါသည်။

ကံမကောင်းစွာပဲ၊ ပျမ်းမျှနှင့် အလယ်အလတ်သည် bimodal ဖြန့်ဖြူးမှုအတွက် သိရန် အသုံးမဝင်ပါ။ ဥပမာ၊ အထက်ဖော်ပြပါ ဥပမာရှိ ကျောင်းသားများ၏ ပျမ်းမျှ စာမေးပွဲရမှတ်မှာ 81 ဖြစ်သည်။

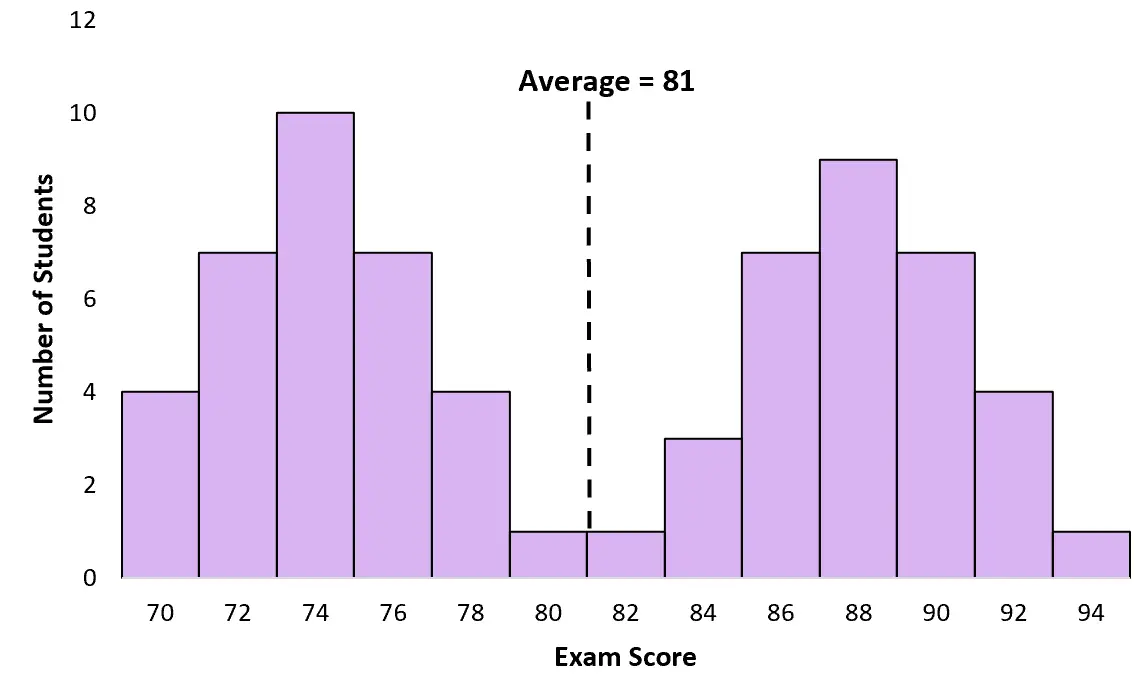
သို့သော်၊ ကျောင်းသားအနည်းငယ်သည် 81 အနီးတွင်မဆို ရမှတ်အလွန်နည်းပါသည်။ ဤကိစ္စတွင်၊ ပျမ်းမျှအားဖြင့် လွဲမှားနေပါသည်။ ကျောင်းသားအများစုသည် အမှန်တကယ် ၇၄ သို့မဟုတ် ၈၈ ဝန်းကျင်တွင် ရမှတ်များ ရှိသည်။

bimodal ဖြန့်ဖြူးမှုများကို ခွဲခြမ်းစိတ်ဖြာပြီး အဓိပ္ပာယ်ဖွင့်ဆိုရန် ပိုမိုကောင်းမွန်သောနည်းလမ်းမှာ ဒေတာများကို သီးခြားအုပ်စုနှစ်ခုအဖြစ် ခွဲခြမ်းပြီး အုပ်စုတစ်ခုစီအတွက် အလယ်တည်နေရာနှင့် ဖြန့်ဖြူးမှုကို ခွဲခြမ်းစိတ်ဖြာရန်ဖြစ်သည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် စာမေးပွဲရလဒ်များကို “ နိမ့်ရမှတ်များ” နှင့် “ မြင့်မားသောရမှတ်များ” အဖြစ် ပိုင်းခြားနိုင်ပြီး အုပ်စုတစ်ခုစီအတွက် ပျမ်းမျှနှင့် စံသွေဖည်မှုကို ရှာဖွေနိုင်သည်။

ပျမ်းမျှ၊ အလယ်အလတ် သို့မဟုတ် စံသွေဖည်မှုကဲ့သို့ ပေးထားသော ဖြန့်ဖြူးမှုအတွက် အကျဉ်းချုပ်စာရင်းအင်းများကို တွက်ချက်သည့်အခါ၊ ၎င်းသည် unimodal သို့မဟုတ် multimodal ဟုတ်မဟုတ် ဆုံးဖြတ်ရန် ဖြန့်ဖြူးမှုကို မြင်သာစေရန် သေချာပါစေ။

ဖြန့်ဝေမှုတစ်ခုသည် ဘက်စုံသုံးပါက၊ ၎င်းကို ဆိုလိုရင်းတစ်ခုတည်း၊ အလယ်အလတ် သို့မဟုတ် စံသွေဖည်မှုကို အသုံးပြု၍ ဖော်ပြရန် လွဲမှားနိုင်သည်။