မူလအားဖြင့် ဆုတ်ယုတ်ခြင်း- အဓိပ္ပါယ်နှင့် ဥပမာ

ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုသည် တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ကြိုတင်ခန့်မှန်းကိန်းရှင်များနှင့် တုံ့ပြန်မှုကိန်းရှင် ကြားရှိ ဆက်နွယ်မှုကို အရေအတွက်သတ်မှတ်ရန် အသုံးပြုနိုင်သည့် နည်းလမ်းတစ်ခုဖြစ်သည်။

ရိုးရှင်းသော linear regression model သည် အောက်ပါပုံစံကို ယူပါသည်။

y = β ₀ + β ₁ x

ရွှေ-

• y : တုံ့ပြန်မှုကိန်းရှင်၏တန်ဖိုး
• β ₀ : x = 0 (“ကြားဖြတ်” ဟူသောအသုံးအနှုန်းဟုခေါ်သောအခါ တုံ့ပြန်မှုကိန်းရှင်၏တန်ဖိုး၊
• β ₁ : x တွင် ယူနစ်တစ်ယူနစ် တိုးခြင်းနှင့် ဆက်စပ်နေသော တုံ့ပြန်မှုကိန်းရှင်တွင် ပျမ်းမျှတိုးနှုန်း
• x : ကြိုတင်ခန့်မှန်းကိန်းရှင်၏တန်ဖိုး

ဤမော်ဒယ်၏ မွမ်းမံထားသော ဗားရှင်းကို မူလအားဖြင့် ဆုတ်ယုတ်မှု ဟု ခေါ်သည်၊ x သည် 0 နှင့် ညီမျှသောအခါ y နှင့် 0 ညီမျှစေရန် တွန်းအားပေးသည်။

ဤမော်ဒယ်အမျိုးအစားသည် အောက်ပါပုံစံဖြစ်သည်။

y = _β1x

ကြားဖြတ်အခေါ်အဝေါ်ကို မော်ဒယ်မှ လုံးဝဖယ်ရှားလိုက်ကြောင်း သတိပြုပါ။

ကြိုတင်ခန့်မှန်းကိန်းရှင်သည် သုညဖြစ်သည့်အခါ တုံ့ပြန်မှုကိန်းရှင်သည် သုညဖြစ်ရမည်ကို သုတေသီများသိရှိသောအခါ ဤပုံစံကို တစ်ခါတစ်ရံတွင် အသုံးပြုပါသည်။

လက်တွေ့ကမ္ဘာတွင်၊ ဤပုံစံကို သစ်တော သို့မဟုတ် ဂေဟဗေဒလေ့လာမှုများ တွင် အများဆုံးအသုံးပြုလေ့ရှိသည်။

ဥပမာအားဖြင့်၊ သုတေသီများသည် သစ်ပင်အမြင့်ကို ခန့်မှန်းရန် သစ်ပင်အဝန်းကို အသုံးပြုနိုင်သည်။ ပေးထားသောအပင်သည် သုညလုံးပတ်ရှိလျှင် ၎င်းသည် သုညအမြင့်ရှိရမည်။

ထို့ကြောင့်၊ ဤဒေတာနှင့် ဆုတ်ယုတ်မှုပုံစံကို တပ်ဆင်သည့်အခါ မူရင်းအသုံးအနှုန်းသည် သုညဖြစ်ရန် အဓိပ္ပာယ်မရှိပေ။

အောက်ဖော်ပြပါ ဥပမာသည် သာမန်ရိုးရှင်းသော မျဉ်းဖြောင့်ဆုတ်ယုတ်မှုပုံစံနှင့် မူလအစမှတစ်ဆင့် ဆုတ်ယုတ်မှုကို အကောင်အထည်ဖော်သည့် စံနမူနာနှင့် ကိုက်ညီသည့် ကွာခြားချက်ကို ပြသသည်။

ဥပမာ- မူလအားဖြင့် ဆုတ်ယုတ်မှု

ဇီဝဗေဒပညာရှင်တစ်ဦးသည် သစ်ပင်အမြင့်ကို ခန့်မှန်းရန် သစ်ပင်အဝန်းကို အသုံးပြု၍ ဆုတ်ယုတ်မှုပုံစံကို အံဝင်ခွင်ကျဖြစ်စေလိုသည်ဆိုပါစို့။ သူမသည် အပြင်သွားကာ သစ်ပင် ၁၅ ပင်၏ နမူနာအတွက် အောက်ပါတိုင်းတာမှုများကို ကောက်ယူသည်။

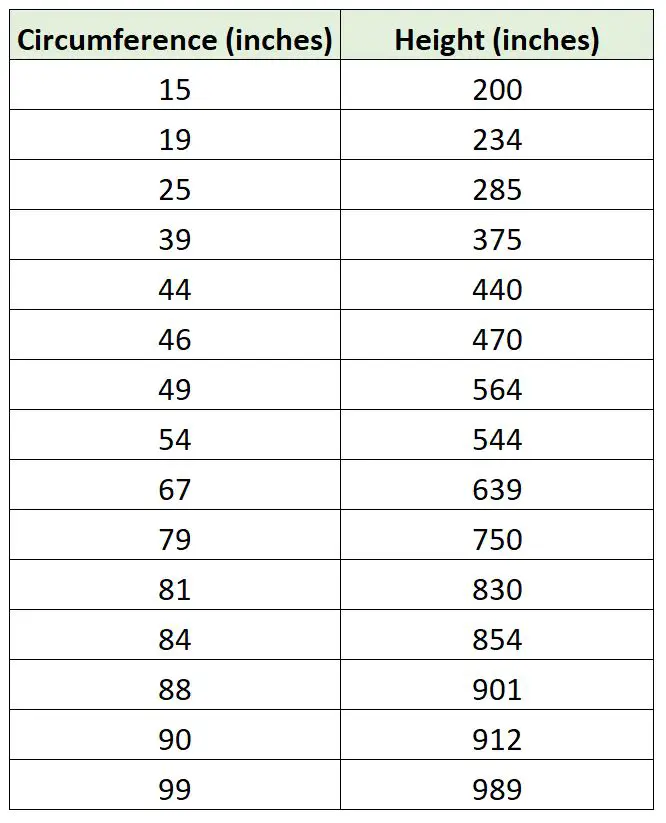
ကြားဖြတ်အသုံးမပြုဘဲ ဆုတ်ယုတ်မှုမျဉ်းနှစ်ကြောင်းကို ပုံဖော်ထားသည့် ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံနှင့် ကိုက်ညီရန် အောက်ပါကုဒ် R တွင် ကျွန်ုပ်တို့အသုံးပြုနိုင်သည်-

 #create data frame
df <- data. frame (circ=c(15, 19, 25, 39, 44, 46, 49, 54, 67, 79, 81, 84, 88, 90, 99),
                 height=c(200, 234, 285, 375, 440, 470, 564, 544, 639, 750, 830, 854,
                          901, 912, 989))

#fit a simple linear regression model
model <- lm(height ~ circ, data = df)

#fit regression through the origin
model_origin <- lm(height ~ 0 + ., data = df)

#create scatterplot
plot(df$circ, df$height, xlab=' Circumference ', ylab=' Height ',
     cex= 1.5 , pch= 16 , ylim=c(0.1000), xlim=c(0.100))

#add the fitted regression lines to the scatterplot
abline(model, col=' blue ', lwd= 2 )
abline(model_origin, lty=' dashed ', col=' red ', lwd= 2 )

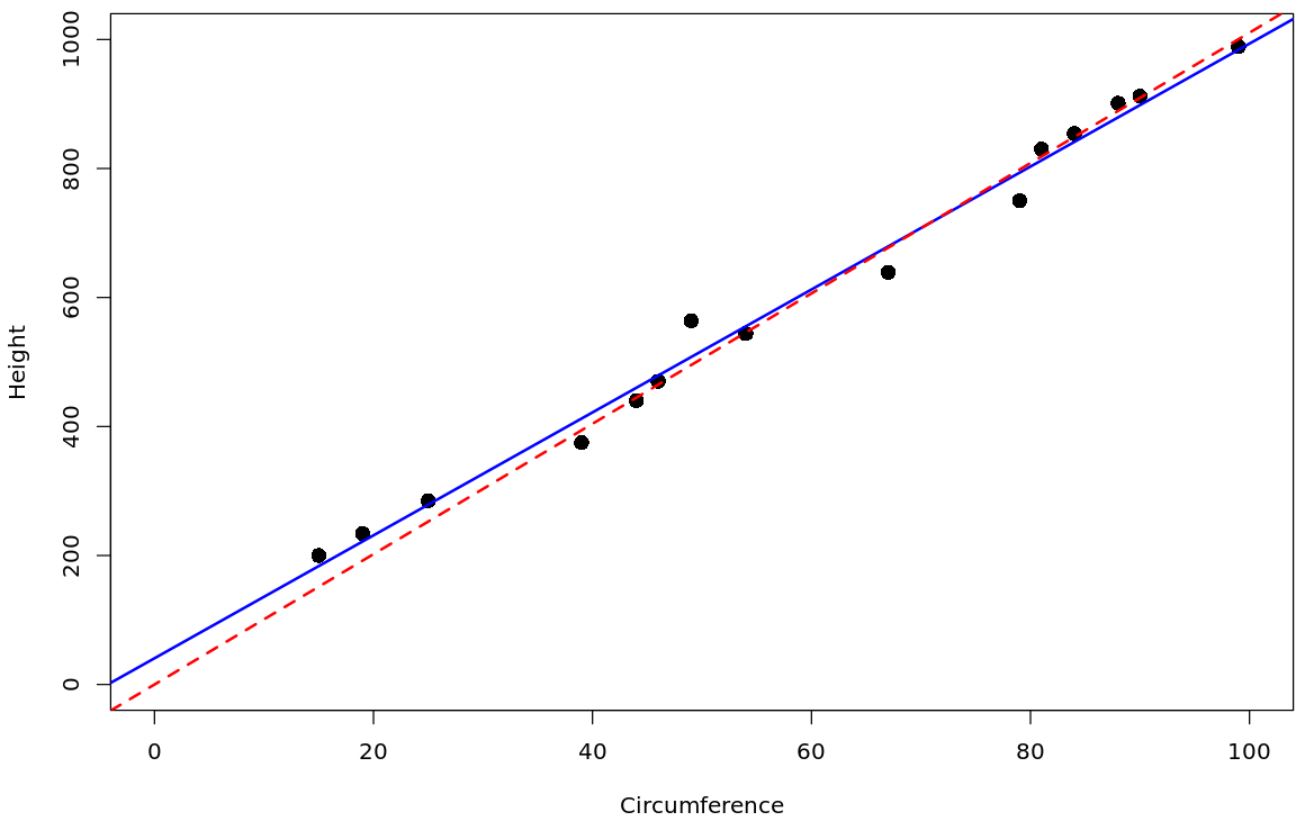
အနီရောင် အစက်ချမျဉ်းသည် မူလဖြတ်သန်းသွားသော ဆုတ်ယုတ်မှုပုံစံကို ကိုယ်စားပြုပြီး အပြာရောင်အစိုင်အခဲမျဉ်းသည် သာမန်ရိုးရိုးမျဉ်းကြောင်းအတိုင်း ဆုတ်ယုတ်မှုပုံစံကို ကိုယ်စားပြုသည်။

မော်ဒယ်တစ်ခုစီအတွက် ဖော်ကိန်း ခန့်မှန်းချက်များကို ရယူရန် R တွင် အောက်ပါကုဒ်ကို အသုံးပြုနိုင်ပါသည်။

 #display coefficients for simple linear regression model
coef(model)

(Intercept) circ 
  40.696971 9.529631 

#display coefficients for regression model through the origin
coef(model_origin)

    circ 
10.10574 

ရိုးရှင်းသော linear regression model အတွက် တပ်ဆင်ထားသော ညီမျှခြင်းမှာ-

အမြင့် = 40.6969 + 9.5296 (လုံးပတ်)၊

မူလအစမှတစ်ဆင့် ဆုတ်ယုတ်မှုပုံစံအတွက် သင့်လျော်သောညီမျှခြင်းမှာ-

အမြင့် = 10.1057 (လုံးပတ်)၊

လုံးပတ်ကိန်းရှင်အတွက် ဖော်ကိန်း ခန့်မှန်းချက်သည် အနည်းငယ်ကွဲပြားကြောင်း သတိပြုပါ။

မူရင်းမှတစ်ဆင့် Regression ကိုအသုံးပြုခြင်းအတွက် ကြိုတင်ကာကွယ်မှုများ

ကြားဖြတ်ဆုတ်ယုတ်မှုကို အသုံးမပြုမီ၊ ခန့်မှန်းသူကိန်းရှင်အတွက် 0 တန်ဖိုးသည် တုံ့ပြန်မှုကိန်းရှင်အတွက် 0 တန်ဖိုးကို ဆိုလိုကြောင်း သေချာစေရမည်။ အခြေအနေများစွာတွင်၊ သေချာစွာသိရန်မှာ မဖြစ်နိုင်သလောက်ပင်။

ဇာစ်မြစ်ကို ခန့်မှန်းရာတွင် လွတ်လပ်မှုအတိုင်းအတာတစ်ခုအထိ ကယ်တင်ရန် အရင်းအမြစ်မှတစ်ဆင့် ဆုတ်ယုတ်ခြင်းကို အသုံးပြုပါက၊ သင်၏နမူနာအရွယ်အစားသည် လုံလောက်ပါက သိသိသာသာ ကွာခြားမှုနည်းပါးပါသည်။

မူလအစမှတစ်ဆင့် ဆုတ်ယုတ်မှုကို သင်အသုံးပြုရန် ရွေးချယ်ပါက၊ သင်၏ ကျိုးကြောင်းဆင်ခြင်မှုကို သင်၏ အပြီးသတ် ခွဲခြမ်းစိတ်ဖြာမှု သို့မဟုတ် အစီရင်ခံစာတွင် သေချာစွာ ဖော်ပြပါ။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် linear regression နှင့်ပတ်သက်သော နောက်ထပ်အချက်အလက်များကို ပေးဆောင်သည်-

Simple Linear Regression နိဒါန်း
Multiple Linear Regression အကြောင်း နိဒါန်း
Regression Table ကို ဘယ်လိုဖတ်ပြီး အဓိပါယ်ရမလဲ