မျှတသောတိကျမှုဟူသည် အဘယ်နည်း။ (အဓိပ္ပါယ် & #038; ဥပမာ)

ဟန်ချက်ညီသော တိကျမှုသည် အမျိုးအစားခွဲခြားမှုပုံစံ တစ်ခု၏ စွမ်းဆောင်ရည်ကို အကဲဖြတ်ရန် ကျွန်ုပ်တို့အသုံးပြုနိုင်သည့် မက်ထရစ်တစ်ခုဖြစ်သည်။

အောက်ပါအတိုင်း တွက်ချက်သည်။

Balanced Accuracy = (Sensitivity + Specificity) / ၂

ရွှေ-

• အာရုံခံစားနိုင်မှု – “ စစ်မှန်သောအပြုသဘောဆောင်နှုန်း” – မော်ဒယ်မှရှာဖွေတွေ့ရှိနိုင်သည့်အပြုသဘောဆောင်သောဖြစ်ရပ်များ၏ရာခိုင်နှုန်း။
• တိကျမှု – “ စစ်မှန်သော အနုတ်လက္ခဏာနှုန်း” – မော်ဒယ်က ရှာဖွေတွေ့ရှိနိုင်သည့် အနုတ်လက္ခဏာဆောင်သည့် ဖြစ်ရပ်များ၏ ရာခိုင်နှုန်း။

အတန်းနှစ်ခုသည် ဟန်ချက်မညီသောအခါတွင် ဤမက်ထရစ်သည် အထူးသဖြင့် အသုံးဝင်သည်၊ ဆိုလိုသည်မှာ အတန်းတစ်ခုသည် အခြားတစ်ခုထက် များစွာပိုနေပါသည်။

အောက်ဖော်ပြပါ ဥပမာသည် လက်တွေ့တွင် မျှတသောတိကျမှုကို တွက်ချက်နည်းကို ပြသပြီး ၎င်းသည် အဘယ်ကြောင့် ဤမျှအသုံးဝင်သော မက်ထရစ်ဖြစ်ရခြင်းကို သရုပ်ပြသည်။

ဥပမာ- မျှတသောတိကျမှုကို တွက်ချက်ခြင်း။

အားကစားလေ့လာသူသည် NBA တွင် မတူညီသော ဘတ်စကက်ဘောကစားသမား ၄၀၀ ကို ရေးဆွဲမည်လား မခန့်မှန်းရန် ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှုပုံစံကို အသုံးပြုသည်ဆိုပါစို့။

အောက်ဖော်ပြပါ ရှုပ်ထွေးမှု matrix သည် မော်ဒယ်မှ ပြုလုပ်သော ခန့်မှန်းချက်များကို အကျဉ်းချုပ်ဖော်ပြသည်-

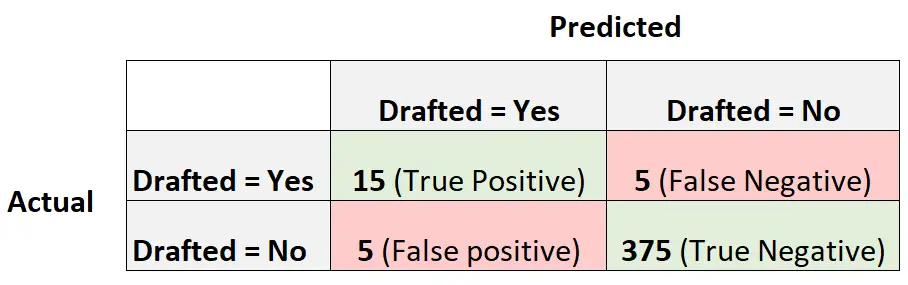
မော်ဒယ်၏ မျှတသောတိကျမှုကို တွက်ချက်ရန်၊ အာရုံခံနိုင်စွမ်းနှင့် တိကျမှုကို ဦးစွာတွက်ချက်ပါမည်-

• အာရုံခံနိုင်စွမ်း : “ စစ်မှန်သော အပြုသဘောနှုန်း” = 15 / (15 + 5) = 0.75
• တိကျမှု – “ စစ်မှန်သော အနုတ်လက္ခဏာနှုန်း” = 375 / (375 + 5) = 0.9868

ထို့နောက် ကျွန်ုပ်တို့သည် မျှတသောတိကျမှုကို အောက်ပါအတိုင်း တွက်ချက်နိုင်သည်။

• Balanced Accuracy = (Sensitivity + Specificity) / ၂
• မျှခြေတိကျမှု = (0.75 + 9868) / 2
• မျှခြေတိကျမှု = 0.8684

မော်ဒယ်၏မျှတသောတိကျမှုသည် 0.8684 ဖြစ်လာသည်။

ဟန်ချက်ညီသောတိကျမှုသည် 1 သို့ပိုမိုနီးကပ်လေလေ၊ မော်ဒယ်သည် စောင့်ကြည့်မှုများကို မှန်ကန်စွာခွဲခြားနိုင်လေလေဖြစ်သည်။

ဤဥပမာတွင်၊ မျှတသောတိကျမှုမှာ အလွန်မြင့်မားသည်၊ ၎င်းသည် ထောက်ပံ့ပို့ဆောင်ရေးဆိုင်ရာ ဆုတ်ယုတ်မှုပုံစံသည် ကောလိပ်ကစားသမားများအား NBA သို့ ရေးဆွဲခြင်းရှိ၊ မရှိကို ခန့်မှန်းရန် အလွန်ကောင်းသောအလုပ်ဖြစ်ကြောင်း ကျွန်ုပ်တို့ကိုပြောပြသည်။

ဤအခြေအနေတွင်၊ အတန်းများသည် အလွန်မျှတမှုမရှိသောကြောင့် (ကစားသမား 20 ဦးကို ရေးဆွဲပြီး 380 ကစားသမားမဟုတ်ပါ)၊ မျှတသောတိကျမှုသည် အလုံးစုံတိကျမှုအတိုင်းအတာတစ်ခုနှင့်နှိုင်းယှဉ်ပါက ကျွန်ုပ်တို့အား မော်ဒယ်စွမ်းဆောင်ရည်၏ ပိုမိုလက်တွေ့ကျသောရုပ်ပုံလွှာကိုပေးပါသည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် အောက်ပါအတိုင်း မော်ဒယ်တိကျမှုကို တွက်ချက်သည်-

• တိကျမှု = (TP + TN) / (TP + TN + FP + FN)
• တိကျမှု = (၁၅+၃၇၅)/(၁၅+၃၇၅+၅+၅)၊
• တိကျမှု = 0.975

မော်ဒယ်၏တိကျမှုသည် 0.975 ဖြစ်ပြီး အလွန်မြင့်မားပုံရသည်။

သို့သော် ကစားသမားတိုင်းသည် အကြမ်းမဖက်ဘဲနေမည်ဟု ရိုးရှင်းစွာ ခန့်မှန်းနိုင်သော မော်ဒယ်ကို သုံးသပ်ကြည့်ပါ။ တိကျမှု 380/400 = 0.95 ရှိသည်။ ၎င်းသည် ကျွန်ုပ်တို့၏ မော်ဒယ်၏ တိကျမှုထက် အနည်းငယ်နိမ့်ပါသည်။

မျှတသောတိကျမှုရမှတ် 0.8684 သည် အတန်းနှစ်ခုစလုံးကို ခန့်မှန်းနိုင်သည့် မော်ဒယ်၏ ပိုမိုကောင်းမွန်သော စိတ်ကူးကို ပေးပါသည်။

တစ်နည်းဆိုရသော်၊ ၎င်းသည် ကျွန်ုပ်တို့အား မည်သည့်ကစားသမားများ အကြမ်းမဖက် ဘဲ မည်သူမည်ဝါဖြစ်မည်ကို ခန့်မှန်းရန် မော်ဒယ်၏စွမ်းရည်ကို ပိုမိုကောင်းမွန်သော အကြံဥာဏ်ကို ပေးသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် မတူညီသော စာရင်းအင်းဆော့ဖ်ဝဲများတွင် ရှုပ်ထွေးမှုမက်ထရစ်ကို ဖန်တီးနည်းကို ရှင်းပြသည်-

Excel တွင် Confusion Matrix ဖန်တီးနည်း
R တွင် ရှုပ်ထွေးမှုမက်ထရစ်ကို ဖန်တီးနည်း
Python တွင် Confusion Matrix ဖန်တီးနည်း