X^2 ၏ မျှော်မှန်းတန်ဖိုးကို တွက်ချက်နည်း

ကျပန်း ကိန်းရှင် X ကို ရည်ညွှန်းသည့် အတွက်၊ သင်သည် X ² ၏ မျှော်မှန်းတန်ဖိုးကို တွက်ချက်ရန် အောက်ပါဖော်မြူလာကို အသုံးပြုနိုင်သည်။

E(X ² ) = Σx ² * p(x)

ရွှေ-

• ∑ : “ပေါင်း” ဟူသော သင်္ကေတ၊
• x : ကျပန်း variable ၏တန်ဖိုး
• p(x) : ကျပန်း variable သည် ပေးထားသောတန်ဖိုးကို ယူသည့်ဖြစ်နိုင်ခြေ

အောက်ဖော်ပြပါ ဥပမာသည် ဤဖော်မြူလာကို လက်တွေ့အသုံးချနည်းကို ပြသထားသည်။

ဥပမာ- X ² ၏ မျှော်မှန်းတန်ဖိုးကို တွက်ချက်ခြင်း။

ကျပန်း variable တစ်ခု၏ ဖြစ်နိုင်ခြေကို ဖော်ပြသော အောက်ပါဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှုဇယားတစ်ခုရှိသည်ဆိုပါစို့၊

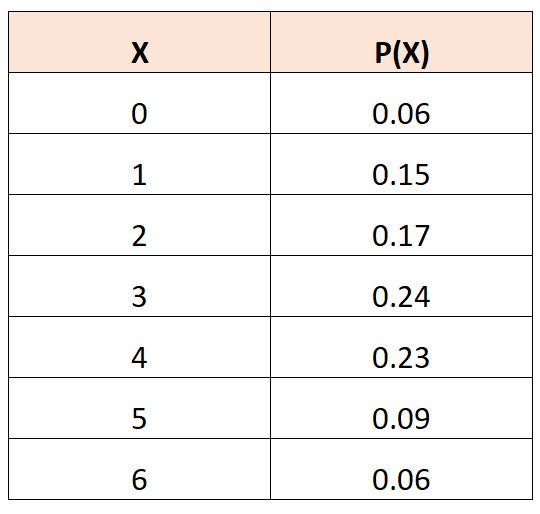
X ² ၏ မျှော်မှန်းတန်ဖိုးကို တွက်ချက်ရန် အောက်ပါဖော်မြူလာကို အသုံးပြုနိုင်ပါသည်။

E(X ² ) = Σx ² * p(x)

E(X ² ) = (0) ² *.06 + (1) ² *.15 + (2) ² *.17 + (3) ² *.24 + (4) ² *.23 + (5) ² *.၀၉ + (၆) ^၂ *.၀၆

E(X ² ) = 0 + 0.15 + 0.68 + 2.16 + 3.68 + 2.25+ 2.16

E( ^X2 ) = 11.08

X ² ၏မျှော်မှန်းတန်ဖိုးမှာ 11.08 ဖြစ်သည်။

ဤကျပန်း variable သည် discrete random variable တစ်ခုဖြစ်ပြီး၊ ဆိုလိုသည်မှာ ၎င်းသည် အကန့်အသတ်ရှိသော တန်ဖိုးများကိုသာ ယူနိုင်သည်ကို သတိပြုပါ။

X သည် စဉ်ဆက်မပြတ် ကျပန်းပြောင်းလဲမှု ဖြစ်ပါက၊ ကျွန်ုပ်တို့သည် X ² ၏မျှော်မှန်းတန်ဖိုးကိုတွက်ချက်ရန် အောက်ပါဖော်မြူလာကို အသုံးပြုရပါမည်။

E(X ² ) = ∫ x ² f(x)dx

ရွှေ-

• ∫- “ပေါင်းစည်းခြင်း” ဟူသော သင်္ကေတ၊
• f(x) : pdf သည် ကျပန်း variable အတွက် ဆက်လက်လုပ်ဆောင်သည်။

စဉ်ဆက်မပြတ် ကျပန်းပြောင်းလဲနိုင်သော ^X2 ၏မျှော်မှန်းတန်ဖိုးကို တွက်ချက်သောအခါ၊ ဤတွက်ချက်မှုကို ကိုယ်တိုင်လုပ်ဆောင်ရန် ပို၍ခက်ခဲနိုင်သောကြောင့် ကျွန်ုပ်တို့သည် ပုံမှန်အားဖြင့် ကိန်းဂဏန်းဆော့ဖ်ဝဲကို အသုံးပြုပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် စာရင်းဇယားများတွင် အခြားဘုံအလုပ်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

ဖြစ်နိုင်ခြေဖြန့်ဝေမှု၏ ဆိုလိုရင်းကို မည်သို့ရှာမည်နည်း။
ဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှု၏ စံသွေဖည်မှုကို မည်သို့ရှာမည်နည်း။
ဖြစ်နိုင်ခြေဖြန့်ဝေမှု၏ကွဲလွဲမှုကို မည်သို့ရှာမည်နည်း။