ဖြစ်နိုင်ခြေ ဖြန့်ဝေမှု မှန်ကန်ခြင်း ရှိ၊ မရှိ ဆုံးဖြတ်နည်း

ဖြစ်နိုင်ခြေ ဖြန့်ဝေမှုသည် အချို့သောတန်ဖိုးများပေါ်တွင် ကျပန်းပြောင်းလွဲချက် တစ်ခုက ဖြစ်နိုင်ခြေကို ပြောပြသည်။

ဖြစ်နိုင်ခြေဖြန့်ဝေမှု မှန်ကန်စေရန်၊ ၎င်းသည် လိုအပ်ချက်နှစ်ခုနှင့် ကိုက်ညီရမည်-

1. ဖြစ်နိုင်ခြေတစ်ခုစီသည် 0 နှင့် 1 ကြားရှိရပါမည်။

2. ဖြစ်နိုင်ခြေ၏ပေါင်းလဒ်သည် 1 အထိ ပေါင်းရပါမည်။

ဤအခြေအနေနှစ်ခုနှင့်ကိုက်ညီပါက ဖြစ်နိုင်ခြေဖြန့်ဝေမှုသည် မှန်ကန်ပါသည်။

အောက်ပါဥပမာများသည် မတူညီသောဖြစ်နိုင်ခြေဖြန့်ဝေမှုများ မှန်ကန်မှုရှိမရှိ စစ်ဆေးနည်းကို ပြသထားသည်။

ဥပမာ 1- ဘောလုံးပွဲတစ်ခုတွင် ဂိုးများသွင်းယူနိုင်ခဲ့သည်။

အောက်ဖော်ပြပါ ဖြစ်နိုင်ခြေ ဖြန့်ဝေမှုသည် ဘောလုံးအသင်းတစ်သင်းသည် ပွဲစဉ်တွင် အချို့သော ဂိုးအရေအတွက်ကို သွင်းယူနိုင်ခြေကို ပြသသည်-

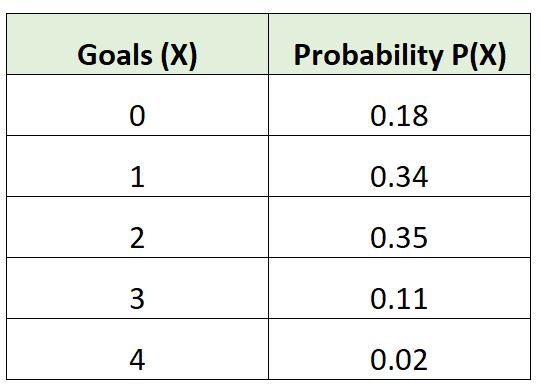
ဤဖြစ်နိုင်ခြေဖြန့်ဝေမှုသည် တရားဝင်ရန် လိုအပ်ချက်နှစ်ခုလုံးနှင့် ကိုက်ညီမှုရှိမရှိ စစ်ဆေးကြည့်ကြပါစို့။

1. ဖြစ်နိုင်ခြေတစ်ခုစီသည် 0 နှင့် 1 ကြားရှိရပါမည်။

တစ်ဦးချင်းစီ၏ ဖြစ်နိုင်ခြေတစ်ခုစီသည် 0 နှင့် 1 ကြားတွင်ရှိသည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။

2. ဖြစ်နိုင်ခြေ၏ပေါင်းလဒ်သည် 1 အထိ ပေါင်းရပါမည်။

ဖြစ်နိုင်ခြေများ၏ပေါင်းလဒ်သည် 1 အထိ ပေါင်းထားသည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်-

ပေါင်း = 0.18 + 0.34 + 0.35 + 0.11 + 0.02 = 1

အခြေအနေနှစ်ခုစလုံးနှင့် ကိုက်ညီသောကြောင့် ဤဖြစ်နိုင်ခြေဖြန့်ဝေမှုသည် မှန်ကန် ပါသည်။

ဥပမာ 2- တစ်လအတွင်း ရောင်းအား

အောက်ပါဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှုသည် ပေးထားသောရောင်းသူသည် လာမည့်လတွင် အချို့သောအရောင်းအရေအတွက်ကို ပြုလုပ်နိုင်သည်ဟူသော ဖြစ်နိုင်ခြေကို ပြသည်-

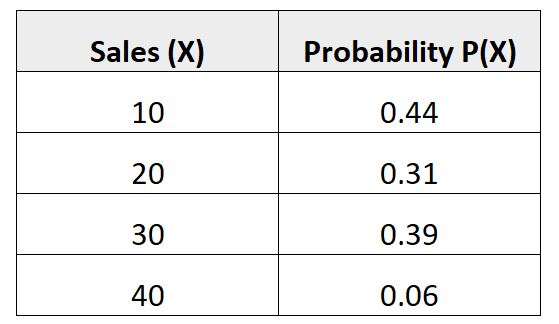
ဤဖြစ်နိုင်ခြေဖြန့်ဝေမှုသည် တရားဝင်ရန် လိုအပ်ချက်နှစ်ခုလုံးနှင့် ကိုက်ညီမှုရှိမရှိ စစ်ဆေးကြည့်ကြပါစို့။

1. ဖြစ်နိုင်ခြေတစ်ခုစီသည် 0 နှင့် 1 ကြားရှိရပါမည်။

တစ်ဦးချင်းစီ၏ ဖြစ်နိုင်ခြေတစ်ခုစီသည် 0 နှင့် 1 ကြားတွင်ရှိသည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။

2. ဖြစ်နိုင်ခြေ၏ပေါင်းလဒ်သည် 1 အထိ ပေါင်းရပါမည်။

ဖြစ်နိုင်ခြေများ၏ ပေါင်းလဒ်သည် 1 အထိ မထည့်ကြောင်း ကျွန်ုပ်တို့မြင်ရသည်-

ပေါင်း = 0.44 + 0.31 + 0.39 + 0.06 = 1.2

အခြေအနေနှစ်ခုလုံးနှင့် မကိုက်ညီသောကြောင့် ဤဖြစ်နိုင်ခြေဖြန့်ဝေမှုသည် မမှန်ကန် ပါ။

ဥပမာ 3- ဘက်ထရီ ချို့ယွင်းမှု အရေအတွက်

အောက်ပါဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှုသည် ပေးထားသောယာဉ်သည် 10 နှစ်တာကာလအတွင်း အချို့သောဘက်ထရီချို့ယွင်းမှုအချို့ကို ကြုံတွေ့ရနိုင်ခြေကို ပြောပြသည်-

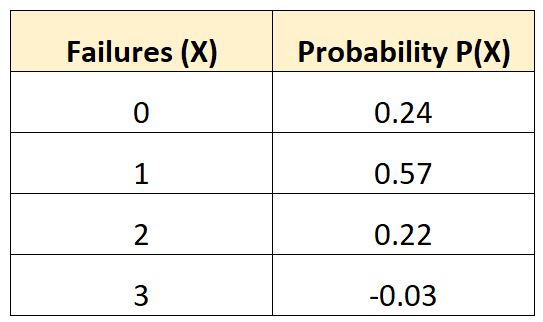
ဤဖြစ်နိုင်ခြေဖြန့်ဝေမှုသည် တရားဝင်ရန် လိုအပ်ချက်နှစ်ခုလုံးနှင့် ကိုက်ညီမှုရှိမရှိ စစ်ဆေးကြည့်ကြပါစို့။

1. ဖြစ်နိုင်ခြေတစ်ခုစီသည် 0 နှင့် 1 ကြားရှိရပါမည်။

တစ်ဦးချင်းစီ၏ဖြစ်နိုင်ခြေသည် 0 နှင့် 1 ကြားမဟုတ်ကြောင်း ကျွန်ုပ်တို့မြင်နိုင်သည်။

ဇယားရှိ နောက်ဆုံးဖြစ်နိုင်ခြေသည် အနုတ်တန်ဖိုးဖြစ်သည်။

2. ဖြစ်နိုင်ခြေ၏ပေါင်းလဒ်သည် 1 အထိ ပေါင်းရပါမည်။

ဖြစ်နိုင်ခြေများ၏ပေါင်းလဒ်သည် 1 အထိ ပေါင်းထားသည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်-

ပေါင်း = 0.24 + 0.57 + 0.22 – 0.03 = 1

အခြေအနေနှစ်ခုလုံးနှင့် မကိုက်ညီသောကြောင့် ဤဖြစ်နိုင်ခြေဖြန့်ဝေမှုသည် မမှန်ကန် ပါ။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် ဖြစ်နိုင်ခြေ ဖြန့်ဝေမှုများအကြောင်း နောက်ထပ် အချက်အလက်များကို ပေးဆောင်သည်-

ဖြစ်နိုင်ခြေဖြန့်ဝေမှု၏ ဆိုလိုရင်းကို မည်သို့ရှာမည်နည်း။
ဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှု ကွဲလွဲမှုကို ဘယ်လိုရှာမလဲ။
ဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှု၏ စံသွေဖည်မှုကို မည်သို့ရှာမည်နည်း။