T စမ်းသပ်မှုမှ p တန်ဖိုးကို ကိုယ်တိုင် တွက်ချက်နည်း

စာရင်းဇယားများတွင် အသုံးအများဆုံးစမ်းသပ်မှုတစ်ခုမှာ t-test ဖြစ်ပြီး၊ လူဦးရေ၏ပျမ်းမျှတန်ဖိုးသည် အချို့သောတန်ဖိုးနှင့်ညီမျှခြင်းရှိမရှိ ဆုံးဖြတ်ရန်အသုံးပြုလေ့ရှိသည်။

ဥပမာအားဖြင့်၊ အပင်မျိုးစိတ်တစ်ခု၏ ပျမ်းမျှအမြင့်သည် 15 လက်မနှင့် ညီမျှသည်ဆိုကြပါစို့။ ၎င်းကိုစမ်းသပ်ရန်၊ ကျွန်ုပ်တို့သည် အပင် 20 ၏ ကျပန်းနမူနာကို စုဆောင်းကာ နမူနာဆိုလိုချက်နှင့် နမူနာစံသွေဖည်မှုကို ရှာဖွေကာ ပျမ်းမျှအရပ်သည် အမှန်တကယ် 15 လက်မရှိမရှိ ဆုံးဖြတ်ရန် t-test ကို လုပ်ဆောင်နိုင်သည်။

စမ်းသပ်မှု၏ null နှင့် အခြားအခြားသော ယူဆချက်များမှာ အောက်ပါအတိုင်းဖြစ်သည် ။

H ₀ : µ = 15

H _a : µ ≠ ၁၅

စမ်းသပ်စာရင်းအင်းအတွက် ဖော်မြူလာမှာ-

t = ( X -μ) / (s/ √n )

x သည် နမူနာဆိုလိုရှိရာ၊ µ သည် hypothetical mean (ကျွန်ုပ်တို့၏ဥပမာတွင် 15 ဖြစ်မည်)၊ s သည် နမူနာစံသွေဖည်ဖြစ်ပြီး n သည် နမူနာအရွယ်အစားဖြစ်သည်။

t တန်ဖိုးကို သိသည်နှင့် သက်ဆိုင်သော p-တန်ဖိုးကို ရှာဖွေရန် ကိန်းဂဏန်းဆော့ဖ်ဝဲ သို့မဟုတ် အွန်လိုင်းဂဏန်းတွက်စက်ကို အသုံးပြုနိုင်သည်။ p-value သည် အချို့သော alpha အဆင့်အောက်တွင် (အများအားဖြင့် ရွေးချယ်မှုများသည် 0.01၊ 0.05၊ နှင့် 0.10)၊ ထို့နောက် null hypothesis ကို ငြင်းပယ်နိုင်ပြီး ပျမ်းမျှအပင်၏ အမြင့်မှာ 15 inches နှင့် မညီမျှ ကြောင်း ကောက်ချက်ချနိုင်ပါသည်။

သို့သော်၊ t-distribution ဇယားကို အသုံးပြု၍ စမ်းသပ် p-value ကို ကိုယ်တိုင် ခန့်မှန်းရန်လည်း ဖြစ်နိုင်သည် ။ ဒီဆောင်းပါးမှာ ဒါကို ဘယ်လိုလုပ်ရမလဲဆိုတာ ရှင်းပြပါမယ်။

ဥပမာ- t-test မှ p-value ကို ကိုယ်တိုင် တွက်ချက်ခြင်း။

ပြဿနာ : အချို့သော အပင်မျိုးစိတ်များ၏ ပျမ်းမျှအမြင့်သည် 15 လက်မနှင့် ညီမျှခြင်းရှိမရှိ Bob သိချင်ပါသည်။ ၎င်းကို စမ်းသပ်ရန်အတွက် အပင် 20 ၏ ကျပန်းနမူနာကို ကောက်ယူပြီး နမူနာဆိုလိုသည်မှာ 14 လက်မဖြစ်ပြီး နမူနာစံသွေဖည်မှုသည် 3 လက်မဖြစ်ကြောင်း တွေ့ရှိခဲ့သည်။ t-test ကို 0.05 ၏ alpha အဆင့်ကို အသုံးပြု၍ စစ်မှန်သော ပျမ်းမျှလူဦးရေ အရပ်သည် အမှန်တကယ် 15 လက်မ ရှိမရှိ ဆုံးဖြတ်ရန်။

ဖြေရှင်းချက်-

အဆင့် 1- null နှင့် အခြားအခြားသော အယူအဆများကို ဖော်ပြပါ။

H ₀ : µ = 15

H _a : µ ≠ ၁၅

အဆင့် 2- စမ်းသပ်စာရင်းအင်းကို ရှာပါ။

t = ( x -μ) / (s/ √n ) = (14-15) / (3/ √20 ) = -1.49

အဆင့် 3- စမ်းသပ်စာရင်းအင်းအတွက် p-value ကိုရှာပါ။

p-value ကို ကိုယ်တိုင်ရှာဖွေရန်၊ လွတ်လပ်မှု၏ n-1 ဒီဂရီရှိသော t-distribution table ကို အသုံးပြုရန် လိုအပ်သည်။ ကျွန်ုပ်တို့၏ဥပမာတွင်၊ ကျွန်ုပ်တို့၏နမူနာအရွယ်အစားမှာ n=20 ဖြစ်ပြီး၊ ထို့ကြောင့် n-1=19 ဖြစ်သည်။

အောက်ဖော်ပြပါ t-distribution ဇယားတွင်၊ ဘယ်ဘက်ခြမ်းရှိ “ 19” နှင့် ကိုက်ညီသော အတန်းကို ကြည့်ရန်နှင့် ကျွန်ုပ်တို့၏ စမ်းသပ်စာရင်းအင်း 1.49 ၏ ပကတိတန်ဖိုးကို ရှာဖွေရန် ကြိုးပမ်းရန်လိုအပ်ပါသည်။

1.49 သည် ဇယားတွင် မပေါ်သော်လည်း ၎င်းသည် တန်ဖိုး 1.328 နှင့် 1.729 နှစ်ခုကြားတွင် ရှိနေသည်ကို သတိပြုပါ။

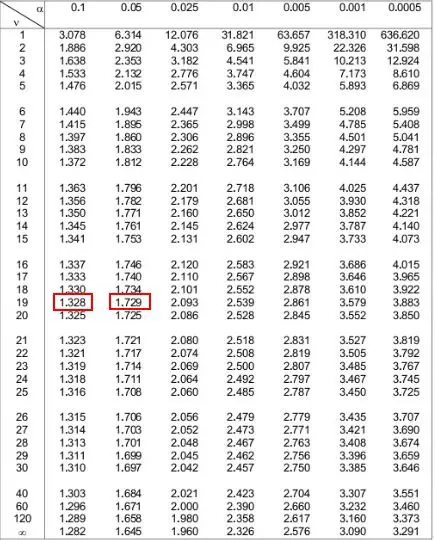
ထို့နောက် ဤနံပါတ်နှစ်ခုနှင့် ကိုက်ညီသော ဇယားထိပ်ရှိ အယ်လ်ဖာအဆင့်နှစ်ခုကို ကျွန်ုပ်တို့ ကြည့်ရှုနိုင်ပါသည်။ ၎င်းတို့သည် 0.1 နှင့် 0.05 ဖြစ်သည် ။

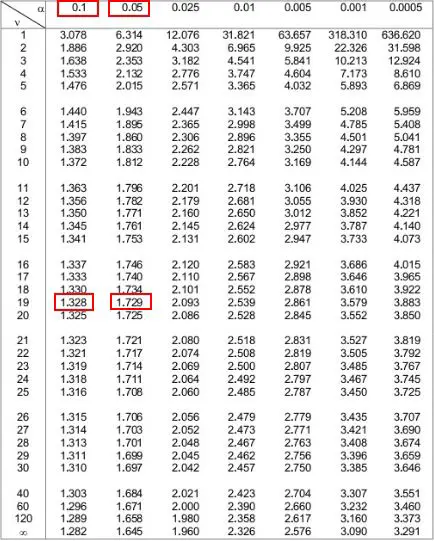
ဆိုလိုသည်မှာ one-tailed test အတွက် p-value သည် 0.1 နှင့် 0.05 ကြားဖြစ်သည်။ အဲဒါကို .075 လို့ ခေါ်ရအောင်။ ကျွန်ုပ်တို့၏ t-test သည် အမြီးနှစ်ကြောင်းဖြစ်သောကြောင့်၊ ဤတန်ဖိုးကို 2 ဖြင့် မြှောက်ရန် လိုအပ်ပါသည်။ ထို့ကြောင့်၊ ကျွန်ုပ်တို့၏ ခန့်မှန်း p-value သည် 0.075*2 = 0.15 ဖြစ်သည်။

အဆင့် 4- ကောက်ချက်ဆွဲပါ။

ဤ p-value သည် ရွေးချယ်ထားသော alpha အဆင့် 0.05 ထက် မ နိမ့်သောကြောင့်၊ null hypothesis ကို ငြင်းပယ်၍မရပါ။ ထို့ကြောင့် ဤအပင်မျိုးစိတ်များ၏ ပျမ်းမျှအမြင့်သည် 15 လက်မမှလွဲ၍ အခြားမည်သည့်အရာဖြစ်သည်ဆိုရန် လုံလောက်သောအထောက်အထားမရှိပါ။

ရလဒ်များကို ဂဏန်းပေါင်းစက်ဖြင့် စစ်ဆေးပါ။

ကျွန်ုပ်တို့၏ ခန့်မှန်းခြေ p-တန်ဖိုးသည် စစ်မှန်သော p-တန်ဖိုးနှင့် မည်မျှနီးစပ်သည်ကို ကြည့်ရန် ကျွန်ုပ်တို့၏ t -test ကိန်းဂဏန်းနှင့် လွတ်လပ်မှုဒီဂရီများကို အွန်လိုင်း p-value ဂဏန်းတွက်စက် တွင် ထည့်သွင်းနိုင်သည်-

စစ်မှန်သော p-တန်ဖိုးသည် 0.15264 ဖြစ်ပြီး ကျွန်ုပ်တို့၏ခန့်မှန်း p-တန်ဖိုး 0.15 နှင့် အတော်လေးနီးစပ်ပါသည်။

နိဂုံး

t-distribution table ကို အသုံးပြု၍ t-test တစ်ခု၏ p-value ကို ကိုယ်တိုင် ခန့်မှန်းရန် ဖြစ်နိုင်ကြောင်း ဤဆောင်းပါးတွင် ကျွန်ုပ်တို့ တွေ့ရှိခဲ့သည်။ သို့သော်လည်း၊ အခြေအနေအများစုတွင် p-value ကိုလက်ဖြင့်တွက်ချက်ရန်ဘယ်တော့မှမလိုအပ်ဘဲ၊ R နှင့် Excel ကဲ့သို့သော statistical software သို့မဟုတ် စာမေးပွဲ၏ p-value အတိအကျကိုရှာဖွေရန် online calculator ကိုသုံးနိုင်သည်။

အထူးသဖြင့် တိကျသေချာသော စာရင်းအင်းလေ့လာမှုများနှင့် လက်တွေ့စမ်းသပ်မှုများတွင် t-test တစ်ခုမှ p-value အတိအကျကို တတ်နိုင်သမျှ အတိအကျရှာဖွေရန် ဂဏန်းပေါင်းစက်ကို သင်အသုံးပြုလိုသော်လည်း သင်ကိုယ်တိုင် ခန့်မှန်းနိုင်သည်မှာ ကောင်းပါတယ်။ လုံးဝလိုအပ်ပါက p-value ကို t-test ။