နှစ်လမ်းသွား anova ကို ကိုယ်တိုင်လုပ်နည်း

နှစ်လမ်းသွား ANOVA ကို အချက်နှစ်ချက် ခွဲပြီး ခွဲထားသော အမှီအခိုကင်းသော အုပ်စုသုံးစု သို့မဟုတ် ထို့ထက်မကသော အုပ်စုများအကြား စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားချက်ရှိမရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည်။

ဤသင်ခန်းစာသည် နှစ်လမ်းသွား ANOVA ကို ကိုယ်တိုင်လုပ်ဆောင်ပုံကို ရှင်းပြထားသည်။

ဥပမာ- လက်ဖြင့် နှစ်လမ်း ANOVA

ရုက္ခဗေဒပညာရှင်တစ်ဦးသည် နေရောင်ခြည်နှင့် ထိတွေ့မှုအကြိမ်ရေကြောင့် အပင်ကြီးထွားမှုအပေါ် လွှမ်းမိုးမှုရှိမရှိ သိချင်သည်ဆိုပါစို့။ သူမသည် အစေ့ ၄၀ ကို စိုက်ပျိုးပြီး နေရောင်ခြည်နှင့် ရေလောင်းအကြိမ်ရေ မတူညီသော အခြေအနေများတွင် တစ်လကြာ ကြီးထွားစေပါသည်။

တစ်လကြာပြီးနောက် အပင်တစ်ပင်ချင်းစီ၏ အမြင့်ကို မှတ်တမ်းတင်သည်။ ရလဒ်များကို အောက်တွင် ပြထားသည်။

အထက်ဖော်ပြပါဇယားတွင် အပင်ငါးပင်ကို အခြေအနေတစ်ခုစီတွင် ပေါင်းစပ်စိုက်ပျိုးထားကြောင်း တွေ့ရပါသည်။

ဥပမာအားဖြင့် အပင်ငါးပင်ကို နေ့စဥ်ရေလောင်းပြီး နေရောင်မရှိသဖြင့် နှစ်လအကြာတွင် အမြင့်မှာ ၄.၈ လက်မ၊ ၄.၄ လက်မ၊ ၃.၂ လက်မ၊ ၃.၉ လက်မနှင့် ၄.၄ လက်မ၊

နှစ်လမ်း ANOVA လုပ်ဆောင်ရန် အောက်ပါအဆင့်များကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။

အဆင့် 1- ပထမအချက်အတွက် စတုရန်း၏ပေါင်းလဒ်ကို တွက်ချက်ပါ (ရေလောင်းအကြိမ်ရေ)

ပထမဦးစွာ အပင် ၄၀ ၏ ပျမ်းမျှအမြင့်ကို တွက်ချက်ပါမည်။

ပျမ်းမျှ = (4.8 + 5 + 6.4 + 6.3 + … + 3.9 + 4.8 + 5.5 + 5.5) / 40 = 5.1525

ထို့နောက်၊ နေ့စဉ် ရေလောင်းသော အပင်အားလုံး၏ ပျမ်းမျှအမြင့်ကို တွက်ချက်ပါမည်။

နေ့စဉ်ပျမ်းမျှ = (4.8 + 5 + 6.4 + 6.3 + … + 4.4 + 4.8 + 5.8 + 5.8) /20 = 5.155

ဆက်လက်၍ တစ်ပတ်လျှင် ရေလောင်းသော အပင်အားလုံး၏ ပျမ်းမျှအမြင့်ကို တွက်ချက်ပါမည်။

အပတ်စဉ် ပျမ်းမျှ = (4.4 + 4.9 + 5.8 + 6 + … + 3.9 + 4.8 + 5.5 + 5.5) /20 = 5.15

ထို့နောက်၊ အောက်ဖော်ပြပါဖော်မြူလာကို အသုံးပြု၍ “ ရေလောင်းကြိမ်နှုန်း” ကိန်းအတွက် နှစ်ထပ်ကိန်းပေါင်းကို တွက်ချက်ပါမည်။

Σn(X _j – X ..) ^၂

ရွှေ-

• n : အုပ်စု j ၏ နမူနာအရွယ်အစား
• Σ : “ ပေါင်း” ဟု အဓိပ္ပာယ်ရသော ဂရိသင်္ကေတ
• X _j : အုပ်စု j ၏ ပျမ်းမျှ
• X .. : ပျမ်းမျှ

ကျွန်ုပ်တို့၏ဥပမာတွင်၊ “ ရေလောင်းကြိမ်နှုန်း” ကိန်းအတွက် လေးထောင့်ကိန်းများကို အောက်ပါအတိုင်း တွက်ချက်ပါသည်- 20(5.155-5.1525) ² + 20(5.15-5.1525) ² = 0.00025

အဆင့် 2- ဒုတိယအချက်အတွက် (နေရောင်ခြည်ထိတွေ့မှု) အတွက် လေးထောင့်ကိန်းပေါင်းကို တွက်ချက်ပါ။

ပထမဦးစွာ အပင် ၄၀ ၏ ပျမ်းမျှအမြင့်ကို တွက်ချက်ပါမည်။

ပျမ်းမျှ = (4.8 + 5 + 6.4 + 6.3 + … + 3.9 + 4.8 + 5.5 + 5.5) / 40 = 5.1525

ထို့နောက် နေနှင့်မထိတွေ့သော အပင်အားလုံး၏ ပျမ်းမျှအမြင့်ကို တွက်ချက်ပါမည်။

နေမပါတဲ့ ပျမ်းမျှ = (4.8 + 4.4 + 3.2 + 3.9 + 4.4 + 4.4 + 4.2 + 3.8 + 3.7 + 3.9) / 10 = 4.07

အမျိုးမျိုးသော နေရောင်ခြည် ထိတွေ့မှုဒဏ်ခံရသော အပင်များ၏ ပျမ်းမျှအမြင့်ကို ရှာဖွေရန် ဤတွက်ချက်မှုကို ထပ်လုပ်ပါမည်။

• နေရောင်ခြည် ပျမ်းမျှ = ၅.၁
• ပျမ်းမျှ ပျမ်းမျှ နေရောင်ခြည် = 5.89
• ပျမ်းမျှ မြင့်မားသော နေရောင်ခြည် = 5.55

ထို့နောက်၊ အောက်ဖော်ပြပါဖော်မြူလာကို အသုံးပြု၍ “ နေရောင်ခြည်ထိတွေ့မှု” ကိန်းဂဏာန်းအတွက် လေးထောင့်ကိန်းပေါင်းကို တွက်ချက်ပါမည်။

Σn(X _j – X ..) ^၂

ရွှေ-

• n : အုပ်စု j ၏ နမူနာအရွယ်အစား
• Σ : “ ပေါင်း” ဟု အဓိပ္ပာယ်ရသော ဂရိသင်္ကေတ
• X _j : အုပ်စု j ၏ ပျမ်းမျှ
• X .. : ပျမ်းမျှ

ကျွန်ုပ်တို့၏ဥပမာတွင်၊ ကျွန်ုပ်တို့သည် အောက်ပါအတိုင်း “ နေရောင်ခြည်ထိတွေ့မှု” ကိန်းအတွက် နှစ်ထပ်ကိန်းပေါင်းကို တွက်ချက်သည်- 10(4.07-5.1525) ² + 10(5.1-5.1525) ² + 10(5.89 -5.1525) ² + 10(5.55-5.1525) ² = 18.76475

အဆင့် 3- အတွင်းရှိ စတုရန်းများပေါင်းကို တွက်ချက်ပါ (အမှား)

ထို့နောက်၊ အကြောင်းရင်းတစ်ခုစီ၏ပေါင်းစပ်မှုနှင့် အပင်အမြင့်တစ်ခုချင်းစီကြားရှိ မတူညီမှုများ၏ နှစ်ထပ်ကိန်းများကို ပေါင်းယူပြီး စတုရန်း၏ပေါင်းလဒ်ကို တွက်ချက်ပါမည်။

ဥပမာအားဖြင့်၊ နေ့စဥ်ရေလောင်းသော အပင်အားလုံး၏ ပျမ်းမျှအမြင့်သည် နေရောင်ခြည်နှင့် မထိတွေ့ဘဲ 4.14 ဖြစ်သည်။ ထို့နောက် အပင်တစ်ပင်ချင်းစီအတွက် မတူညီသော နှစ်ထပ်ကိန်းများကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။

• နေ့စဥ်ရေလောင်းခြင်းအတွက် SS : (4.8-4.14) ² + (4.4-4.14) ² + (3.2-4.14) ² + (3.9-4.14) ² + (4.4-4.14) ² = 1.512

အချက်များ၏ ပေါင်းစပ်မှုတစ်ခုစီအတွက် ဤလုပ်ငန်းစဉ်ကို ကျွန်ုပ်တို့ ပြန်လုပ်နိုင်ပါသည်။

• နေ့စဥ်ရေလောင်းခြင်းနှင့် နေရောင်ခြည်နည်းခြင်းအတွက် SS- 0.928
• နေ့စဉ်ရေလောင်းခြင်းနှင့် ပျမ်းမျှနေရောင်ခြည်အတွက် SS: 1,788
• နေ့စဉ်ရေလောင်းခြင်းနှင့် ပြင်းထန်သောနေရောင်ခြည်အတွက် SS- 1.648
• နေမ၀င်ဘဲ အပတ်စဉ် ရေလောင်းရန် SS: 0.34
• အပတ်စဉ် ရေလောင်းခြင်းနှင့် နေရောင်ခြည်နည်းခြင်းအတွက် SS- 0.548
• အပတ်စဉ်ရေလောင်းခြင်းနှင့် ပျမ်းမျှနေရောင်ခြည်အတွက် SS – 0.652
• အပတ်စဉ် ရေလောင်းခြင်းနှင့် ပြင်းထန်သော နေရောင်ခြည်အတွက် SS – 1,268

ထို့နောက် ကျွန်ုပ်တို့သည် ဤတန်ဖိုးများအားလုံး၏ ပေါင်းလဒ်ကို ကိန်းစတုရန်း၏ပေါင်းလဒ်ကိုရှာရန် (အမှား)။

အတွင်း နှစ်ထပ်ကိန်းများ = 1.512 + 0.928 + 1.788 + 1.648 + 0.34 + 0.548 + 0.652 + 1.268 = 8.684

အဆင့် 4- စတုရန်းများ စုစုပေါင်းကို တွက်ချက်ပါ။

ထို့နောက် အပင်တစ်ခုစီ၏ အမြင့်နှင့် ကြီးကျယ်သော ပျမ်းမျှကြားရှိ ကွာခြားချက်များကို ပေါင်းယူခြင်းဖြင့် စတုရန်း၏ စုစုပေါင်း ပေါင်းလဒ်ကို တွက်ချက်နိုင်သည်-

စုစုပေါင်း နှစ်ထပ်ကိန်း = (4.8 – 5.1525) ² + (5 – 5.1525) ² + … + (5.5 – 5.1525) ² = 28.45975

အဆင့် 5- စတုရန်း အပြန်အလှန် သက်ရောက်မှုကို တွက်ချက်ပါ။

ထို့နောက်၊ အောက်ပါဖော်မြူလာကို အသုံးပြု၍ စတုရန်း အပြန်အလှန် ပေါင်းလဒ်ကို တွက်ချက်ပါမည်။

• အပြန်အလှန်အကျိုးသက်ရောက်မှု SS = SS စုစုပေါင်း – SS Factor 1 – SS Factor 2 – SS အတွင်းခန်း
• SS အပြန်အလှန်တုံ့ပြန်မှု = 28.45975 – 0.00025 – 18.76475 – 8.684
• SS အပြန်အလှန် = 1.01075

အဆင့် 6: ANOVA ဇယားကို အပြီးသတ်ပါ။

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် နှစ်လမ်းသွား ANOVA ဇယားမှ တန်ဖိုးများကို ဖြည့်ပါမည်-

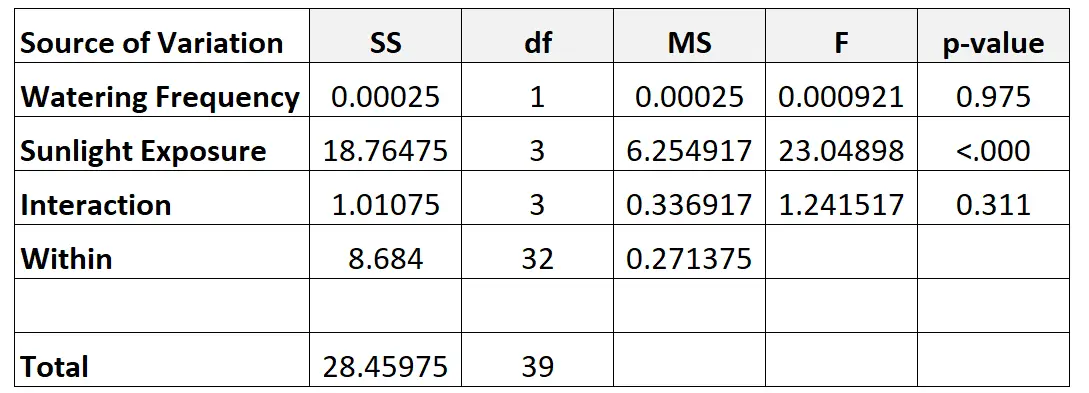
ဤသည်မှာ ဇယားရှိ မတူညီသော ဂဏန်းများကို တွက်ချက်ပုံဖြစ်သည် ။

• df ရေလောင်းအကြိမ်ရေ- d-1 = 2-1 = 1
• df Sun exposure: k-1 = 4-1 = 3
• dfInteraction : (j-1)*(k-1) = 1*3 = 3
• df In : n – (j*k) = 40 – (2*4) = 32
• စုစုပေါင်း df: n-1 = 40-1 = 39
• MS- SS/DF
• ရေလောင်းအကြိမ်ရေ F : အိမ်တွင်း MS/MS ရေလောင်းအကြိမ်ရေ
• F နေရောင်ခြည်ထိတွေ့မှု : MS / MS နေရောင်ခြည် ထိတွေ့မှု အိမ်တွင်း
• အပြန်အလှန်တုံ့ပြန်မှု F : အပြန်အလှန်တုံ့ပြန်မှု MS / MS အတွင်း
• p-value ရေလောင်းအကြိမ်ရေ : ပိုင်းဝေ df = 1 နှင့် ပိုင်းခြေ df = 32 ၏ F-တန်ဖိုး 0.000921 နှင့် သက်ဆိုင်သည့် p-တန်ဖိုး
• နေရောင်ခြည်ထိတွေ့မှု p-တန်ဖိုး : ပိုင်းဝေ df = 3 နှင့် ပိုင်းခြေ df = 32 ၏ F-တန်ဖိုး 23.04898 နှင့် သက်ဆိုင်သည့် p-တန်ဖိုး
• p-တန်ဖိုး အပြန်အလှန်တုံ့ပြန်မှု – ပိုင်းဝေ df = 3 နှင့် ပိုင်းခြေ df = 32 နှင့် 1.241517 ၏ F-တန်ဖိုးနှင့် သက်ဆိုင်သည့် p-တန်ဖိုး

မှတ်ချက် #1- n = ရှုမြင်မှုစုစုပေါင်းအရေအတွက်၊ j = ရေလောင်းအကြိမ်ရေအတွက် အဆင့်အရေအတွက်၊ k = နေရောင်ခြည်ထိတွေ့မှုအတွက် အဆင့်အရေအတွက်။

မှတ်ချက် #2 : F-value နှင့် ကိုက်ညီသော p-တန်ဖိုးများကို F-distribution calculator ဖြင့် တွက်ချက်ထားပါသည်။

အဆင့် 7- ရလဒ်များကို ဘာသာပြန်ပါ။

ANOVA ဇယားမှ အောက်ပါတို့ကို ကျွန်ုပ်တို့ ကြည့်ရှုနိုင်ပါသည်။

• ရေလောင်းအကြိမ်ရေနှင့် နေရောင်ခြည်ထိတွေ့မှုကြား အပြန်အလှန်အကျိုးသက်ရောက်မှုအတွက် p-တန်ဖိုးသည် 0.311 ဖြစ်သည်။ ၎င်းသည် α = 0.05 တွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားခြင်းမရှိပါ။
• ရေလောင်းအကြိမ်ရေအတွက် p-တန်ဖိုးသည် 0.975 ဖြစ်သည်။ ၎င်းသည် α = 0.05 တွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားသည် မဟုတ်ပါ။
• နေရောင်ခြည်ထိတွေ့မှုအတွက် p-တန်ဖိုးသည် <0.000 ဖြစ်သည်။ ၎င်းသည် α = 0.05 တွင် စာရင်းအင်းအရ သိသာထင်ရှားသည်။

ဤရလဒ်များသည် အပင်အမြင့်အပေါ် ကိန်းဂဏန်းအရ သိသာထင်ရှားသော အကျိုးသက်ရောက်မှုရှိသော တစ်ခုတည်းသောအချက်မှာ နေရောင်ခြည်နှင့်ထိတွေ့ခြင်းဖြစ်သည်ဟု ဖော်ပြသည်။

အပြန်အလှန်သက်ရောက်မှုမရှိသောကြောင့်၊ နေရောင်ခြည်ထိတွေ့မှု၏အကျိုးသက်ရောက်မှုသည် ရေလောင်းအကြိမ်ရေအဆင့်တစ်ခုစီတွင် တစ်သမတ်တည်းဖြစ်သည်။

ရိုးရိုးရှင်းရှင်းပြောရလျှင် အပင်တစ်ပင်ကို နေ့စဉ် သို့မဟုတ် အပတ်စဉ် ရေလောင်းသည်ဖြစ်စေ နေရောင်ထိတွေ့မှုသည် အပင်အပေါ် သက်ရောက်မှုမရှိပေ။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် ANOVA များအကြောင်း နောက်ထပ်အချက်အလက်များကို ပေးဆောင်သည်-

တစ်လမ်းမောင်း ANOVA ကို ကိုယ်တိုင်လုပ်ဆောင်နည်း
ANOVA ထပ်ခါတလဲလဲ အစီအမံများကို ကိုယ်တိုင်လုပ်ဆောင်နည်း
လမ်းညွှန်ချက်အပြည့်အစုံ- နှစ်လမ်းသွား ANOVA ရလဒ်များကို မည်သို့အစီရင်ခံမည်နည်း။