မျဉ်းကြောင်းအတိုင်း ဆုတ်ယုတ်မှုများစွာကို လက်ဖြင့် (တစ်ဆင့်ပြီးတစ်ဆင့်)
Multiple linear regression သည် ကြိုတင်ခန့်မှန်းကိန်းရှင် နှစ်ခု သို့မဟုတ် ထို့ထက်ပိုသော ကိန်းရှင်များနှင့် တုံ့ပြန်မှု ကိန်းရှင် တစ်ခုကြားရှိ ဆက်နွယ်မှုကို တွက်ချက်ရန် ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည့် နည်းလမ်းတစ်ခုဖြစ်သည်။
ဤသင်ခန်းစာတွင် မျဉ်းကြောင်းလိုက် ဆုတ်ယုတ်မှုများစွာကို ကိုယ်တိုင်လုပ်ဆောင်နည်းကို ရှင်းပြထားသည်။
ဥပမာ- လက်ဖြင့် မျဉ်းကြောင်း ဆုတ်ယုတ်မှု အများအပြား
ကျွန်ုပ်တို့တွင် တုံ့ပြန်မှုကိန်းရှင် y နှင့် ကြိုတင်ခန့်မှန်းကိန်းရှင် x 1 နှင့် x 2 နှစ်ခုပါရှိသည်ဆိုပါစို့။
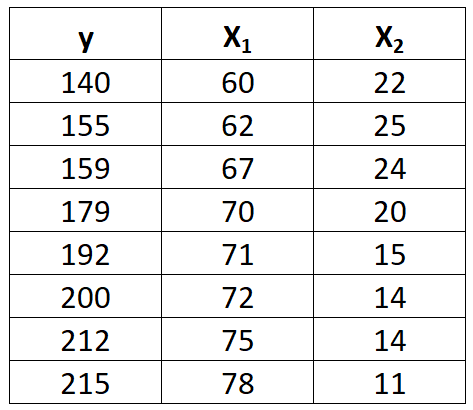
ဤဒေတာအတွဲအတွက် မျဉ်းကြောင်းအတိုင်း ဆုတ်ယုတ်မှုပုံစံမျိုးစုံကို အံဝင်ခွင်ကျဖြစ်စေရန် အောက်ပါအဆင့်များကို ဖြည့်စွက်ပါ။
အဆင့် 1- x 1 2 ၊ x 2 2 ၊ x 1 y ၊ x 2 y နှင့် x 1 x 2 တို့ကို တွက်ချက်ပါ။
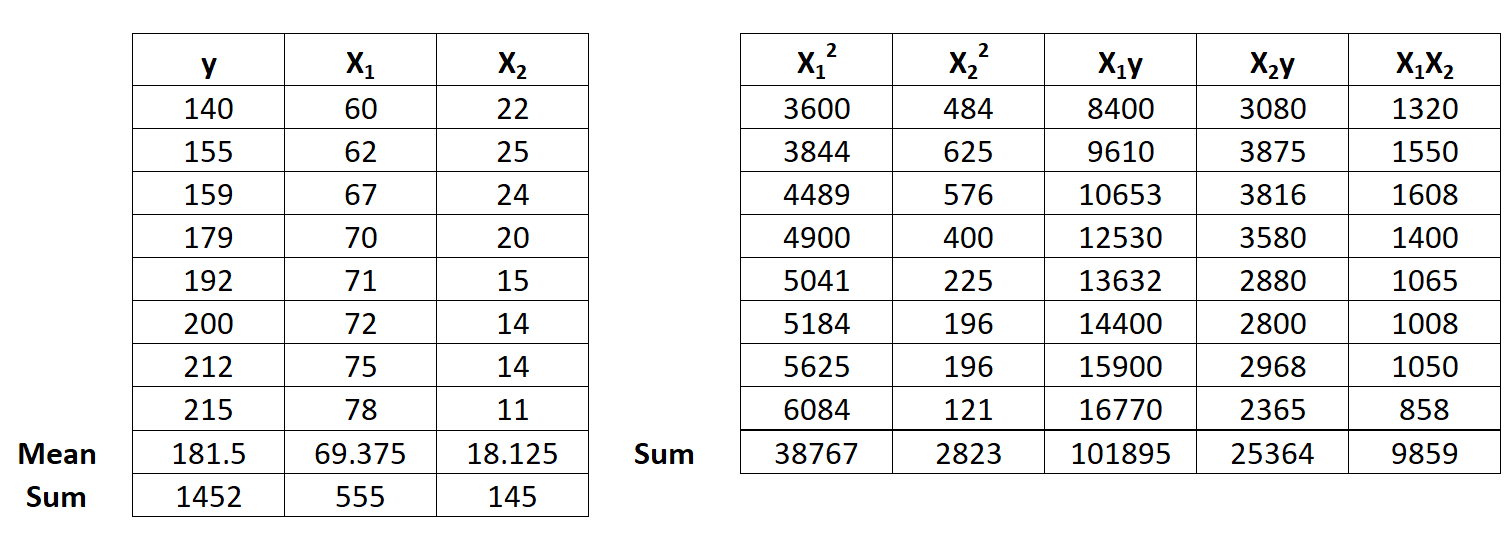
အဆင့် 2- ဆုတ်ယုတ်မှုပေါင်းများကို တွက်ချက်ပါ။
ထို့နောက်၊ အောက်ဖော်ပြပါ ဆုတ်ယုတ်မှုပေါင်းလဒ်တွက်ချက်မှုများကို လုပ်ဆောင်ပါ-
- Σx12 = ΣX12 – ( ΣX1 ) 2 / n = 38.767 – (555) 2/8 = 263.875
- Σx22 = ΣX22 – ( ΣX2 ) 2 / n = 2823 – (145) 2/8 = 194.875
- Σ x 1 y = ∑
- Σ x 2 y = ∑
- Σ x 1 x 2 = ∑
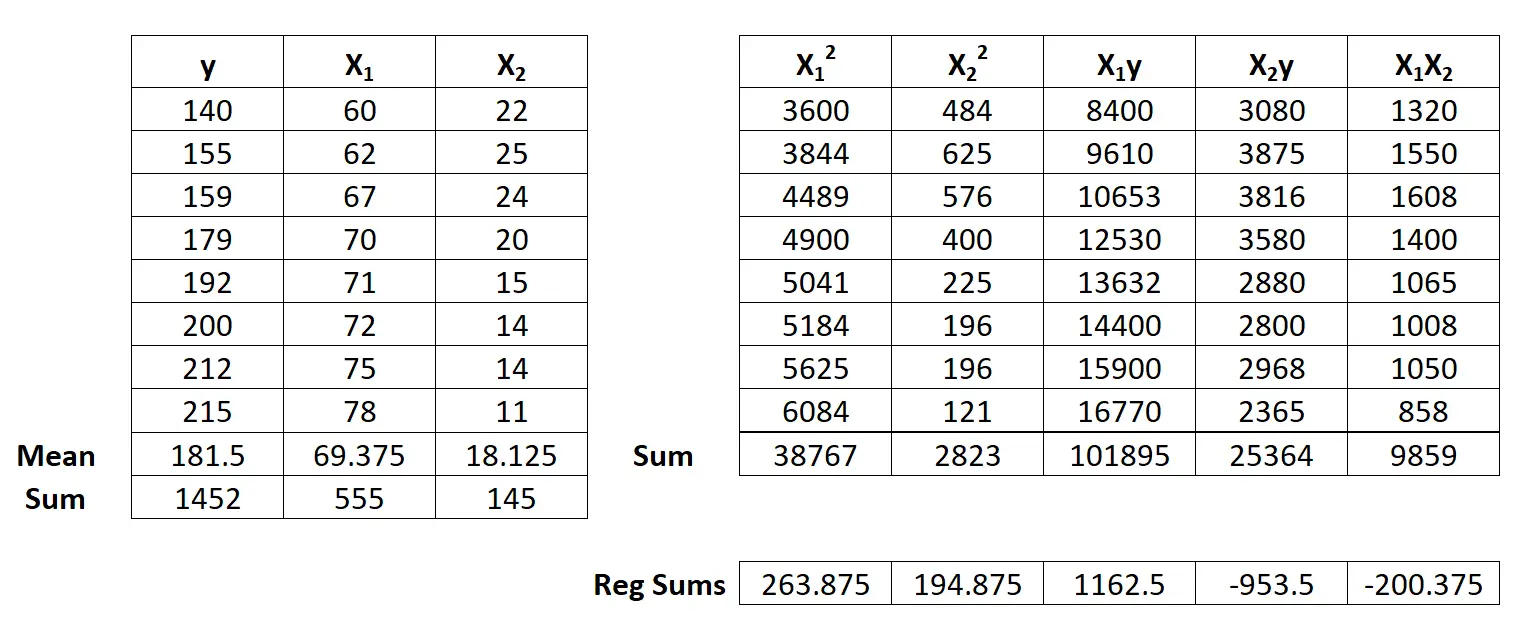
အဆင့် 3- b 0 ၊ b 1 နှင့် b 2 ကို တွက်ချက်ပါ။
b 1 ကို တွက်ချက်ရန် ဖော်မြူလာမှာ- [(Σx 2 2 )(Σx 1 y) – (Σx 1 x 2 )(Σx 2 y )] / [(Σx 1 2 )(Σx 2 ) – (Σx 1 x 2 ) 2 ]
ဒီတော့ b 1 = [(194.875)(1162.5) – (-200.375)(-953.5)] / [(263.875) (194.875) – (-200.375) 2 ] = 3.148
b 2 ကို တွက်ချက်ရန် ဖော်မြူလာမှာ- [(Σx 1 2 )(Σx 2 y ) – (Σx 1 x 2 )(Σx 1 y)] / [(Σx 1 2 )(Σx 2 ) – (Σx 1 x 2 ) 2 ]
ဒီတော့ b 2 = [(263.875)(-953.5) – (-200.375)(1152.5)] / [(263.875) (194.875) – (-200.375) 2 ] = -1.656
b 0 တွက်ချက်ရန် ဖော်မြူလာမှာ y – b 1 X 1 – b 2 X 2
ထို့ကြောင့် b 0 = 181.5 – 3.148(69.375) – (-1.656)(18.125) = -6.867
အဆင့် 5- b 0 ၊ b 1 နှင့် b 2 ကို ခန့်မှန်းမျဉ်းကြောင်းဆုတ်ယုတ်မှုညီမျှခြင်းထဲသို့ ထည့်ပါ။
ခန့်မှန်း linear regression equation သည်- ŷ = b 0 + b 1 *x 1 + b 2 *x 2
ကျွန်ုပ်တို့၏ဥပမာတွင်၊ ၎င်းသည် ŷ = -6.867 + 3.148x 1 – 1.656x 2 ဖြစ်သည်။
Multiple linear regression equation ကို ဘယ်လိုအဓိပ္ပာယ်ဖွင့်မလဲ။
ဤတွင် ခန့်မှန်းခြေမျဉ်းကြောင်းဆုတ်ယုတ်မှုညီမျှခြင်းအား အဓိပ္ပါယ်ဖွင့်ဆိုပုံဖြစ်ပါသည်- ŷ = -6.867 + 3.148x 1 – 1.656x 2
b0 = -6.867 ။ ကြိုတင်ခန့်မှန်းကိန်းရှင်နှစ်ခုလုံးသည် သုညနှင့်ညီမျှသောအခါ၊ ပျမ်းမျှတန်ဖိုး y သည် -6.867 ဖြစ်သည်။
b1 = 3.148 ။ x 1 တွင် တစ်ယူနစ် တိုးခြင်းသည် ပျမ်းမျှအားဖြင့် y တွင် 3.148 ယူနစ် တိုးခြင်းနှင့် ဆက်စပ်နေသည်၊ x 2 သည် အမြဲမပြတ်ရှိနေသည်ဟု ယူဆပါသည်။
b2 = -1.656 ။ x 2 တွင် တစ်ယူနစ် တိုးခြင်းသည် y တွင် 1,656 ယူနစ် ကျဆင်းခြင်းနှင့် ဆက်စပ်နေသည်၊ ပျမ်းမျှအားဖြင့် x 1 သည် စဉ်ဆက်မပြတ် ရှိနေသည်ဟု ယူဆပါသည်။
ထပ်လောင်းအရင်းအမြစ်များ
Multiple Linear Regression အကြောင်း နိဒါန်း
ရိုးရှင်းသော linear regression ကို လက်ဖြင့်ပြုလုပ်နည်း
စာရေးသူအကြောင်း
Benjamin Anderson
မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။