လော့ဂရစ်သမ် ဆုတ်ယုတ်မှု

ဤဆောင်းပါးတွင် logarithmic regression သည် မည်သည့်အရာနှင့် လုပ်ဆောင်ကြောင်းကို ရှင်းပြထားသည်။ ထို့အပြင်၊ သဘောတရားကို အပြည့်အဝနားလည်ရန် logarithmic regression ၏ ဥပမာကို သင်တွေ့မြင်နိုင်ပါသည်။

လော့ဂရစ်သမ် ဆုတ်ယုတ်ခြင်းဟူသည် အဘယ်နည်း။

လော့ဂရစ်သမ်ဆုတ်ယုတ်မှု သည် ၎င်း၏ညီမျှခြင်းတွင် လော့ဂရစ်သမ်ပါ၀င်သည့် ဆုတ်ယုတ်မှုပုံစံတစ်ခုဖြစ်သည်။ အထူးသဖြင့်၊ လော့ဂရစ်သမ်ဆုတ်ယုတ်မှုတွင် လွတ်လပ်သောကိန်းရှင်၏ လော့ဂရစ်သမ်ကို ယူသည်။ ထို့ကြောင့် လော့ဂရစ်သမ်ဆုတ်ယုတ်မှုပုံစံအတွက် ညီမျှခြင်းမှာ y=a+bln(x) ဖြစ်သည်။

နမူနာဒေတာသည် လော့ဂရစ်သမ်မျဉ်းကွေးကို ဖွဲ့စည်းသည့်အခါ လော့ဂရစ်သမ်ဆုတ်ယုတ်မှုပုံစံသည် ဆုတ်ယုတ်မှုပုံစံတစ်ခုကို အံဝင်ခွင်ကျဖြစ်စေရန်အတွက် အလွန်အသုံးဝင်သည်၊ ထို့ကြောင့် ဆုတ်ယုတ်မှုပုံစံသည် နမူနာဒေတာနှင့် ပိုကိုက်ညီစေရန်အတွက် အလွန်အသုံးဝင်သည်။ သင်သည် လော့ဂရစ်သမ် ဆုတ်ယုတ်မှုကို မည်သည့်အချိန်တွင် လုပ်ဆောင်သင့်သည်ကို အောက်တွင် ကျွန်ုပ်တို့ မြင်တွေ့ရပါမည်။

ထို့ကြောင့်၊ logarithmic regression သည် exponential regression နှင့် polynomial regression တို့ကဲ့သို့ linear မဟုတ်သော regression အမျိုးအစားတစ်ခုဖြစ်သည်။

လော့ဂရစ်သမ် ဆုတ်ယုတ်မှု ဖော်မြူလာ

လော့ဂရစ်သမ် ဆုတ်ယုတ်မှုပုံစံတွင် အမှီအခိုကင်းသော ကိန်းရှင်၏ လော့ဂရစ်သမ်ကို ရယူခြင်း ပါဝင်သည်။ ထို့ကြောင့်၊ logarithmic regression ၏ညီမျှခြင်းအတွက်ဖော်မြူလာ မှာ y=a+b·ln(x) ဖြစ်သည်။

ရွှေ-

• 

  dependent variable ဖြစ်ပါတယ်။

• 

  လွတ်လပ်သောကိန်းရှင်ဖြစ်သည်။

• 

  regression coefficients တွေပါ။

y=a+b·ln(x) သည် အမှန်တကယ်တွင် မျဉ်းတစ်ခု၏ ညီမျှခြင်းဖြစ်သည်ကို သတိပြုပါ၊ သို့သော် မူရင်းကိန်းရှင် x နှင့် y ကို ရည်ညွှန်းမည့်အစား ၎င်းသည် ln(x) နှင့် y တို့ကို ရည်ညွှန်းပါသည်။

လော့ဂရစ်သမ် ဆုတ်ယုတ်မှုကို ဘယ်အချိန်မှာ လုပ်မလဲ။

နမူနာဒေတာ၏ဂရပ်သည် လော့ဂရစ်သမ်မျဉ်းကွေးဖြစ်သောအခါ၊ ဆိုလိုသည်မှာ အမှတ်များ၏ကွက်ကွက်သည် လော့ဂရစ်သမ်လုပ်ဆောင်မှု၏ဂရပ်နှင့် ဆင်တူသောအခါတွင် ကျွန်ုပ်တို့သည် လော့ဂရစ်သမ်ဆုတ်ယုတ်မှုကို လုပ်ဆောင်ရန် လိုအပ်သည်။

အောက်တွင်ဖော်ပြထားသော scatterplot ကိုကြည့်ပါ၊ linear regression model ကို dataset တစ်ခုတွင်တပ်ဆင်ထားသည်။ သင်တွေ့မြင်ရသည့်အတိုင်း မျဉ်းသည် ဒေတာ၏ အနီးစပ်ဆုံး ဆိုးရွားသော အနီးစပ်ဆုံးမဟုတ်သော်လည်း၊ သင်သတိပြုမိပါက၊ အဆုံးတွင်ထက် ဂရပ်ဖ်၏အစတွင် တန်ဖိုးများသည် ပိုမိုလျင်မြန်စွာ တိုးလာသောကြောင့် မျဉ်းသည် လေ့လာတွေ့ရှိချက်များနှင့် လုံးဝကိုက်ညီမှုမရှိပါ။ .

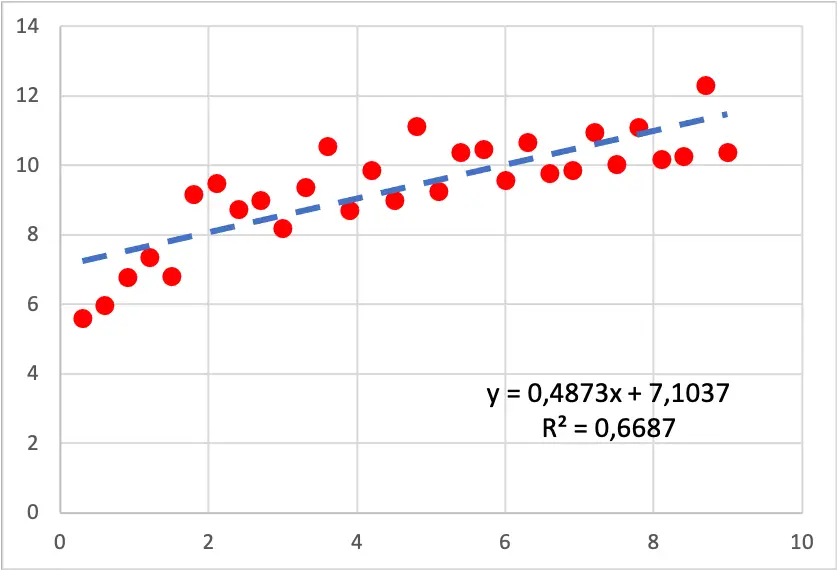
ထို့ကြောင့် ဒေတာသည် လော့ဂရစ်သမ်မျဉ်းကွေးကို လိုက်နာပုံပေါ်သောကြောင့် လော့ဂရစ်သမ်ဆုတ်ယုတ်မှုပုံစံကို ဖန်တီးရန် ကြိုးစားရကျိုးနပ်သည်။ လော့ဂရစ်သမ်ဆုတ်ယုတ်မှုပုံစံမှရရှိသောရလဒ်မှာ အောက်ပါအတိုင်းဖြစ်သည်။

ယခင်ဂရပ်တွင် သင်တွေ့မြင်ရသည့်အတိုင်း၊ ရရှိလာသော လော့ဂရစ်သမ်ဆုတ်ယုတ်မှုပုံစံသည် နမူနာဒေတာနှင့် ပိုမိုကိုက်ညီပါသည်။ အမှန်တကယ်တွင်၊ ဆုံးဖြတ်ခြင်း၏ကိန်းဂဏန်းသည် 66.87% မှ 80.05% သို့ တိုးလာသောကြောင့် မော်ဒယ်သည် ဒေတာနမူနာကို ပိုမိုကောင်းမွန်စွာ ရှင်းပြနိုင်ပါပြီ။ ထို့ကြောင့်၊ ဤကိစ္စတွင်၊ ဒေတာတန်ဖိုးအနီးစပ်ဆုံးညီမျှခြင်းကိုရှာဖွေရန် logistic regression ကိုအသုံးပြုခြင်းသည် ပိုကောင်းသည်။

အခြားလိုင်းမဟုတ်သော ဆုတ်ယုတ်မှုအမျိုးအစားများ

nonlinear regression ၏ အဖြစ်အများဆုံး ဖြစ်ရပ်သုံးခုမှာ-

• လော့ဂရစ်သမ်ဆုတ်ယုတ်မှု – လွတ်လပ်သောကိန်းရှင်၏ လော့ဂရစ်သမ်ကို ယူသည်။
• Exponential regression : အမှီအခိုကင်းသော ကိန်းရှင်သည် ညီမျှခြင်း၏ ထပ်ကိန်းဖြစ်သည်။
• Polynomial Regression : ဆုတ်ယုတ်မှုပုံစံ ညီမျှခြင်းသည် ပေါင်းကိန်းတစ်ခု၏ ပုံစံဖြစ်သည်။