R တွင် လေးပုံတပုံ ဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်နည်း

ကိန်းရှင်နှစ်ခုသည် linear ဆက်ဆံရေးတစ်ခုရှိသောအခါ၊ ၎င်းတို့၏ဆက်နွယ်မှုကို တွက်ချက်ရန် ရိုးရှင်းသော linear regression ကို အသုံးပြုနိုင်သည်။

သို့သော်၊ ကိန်းရှင်နှစ်ခုသည် လေးထောင့်ပုံစံ ဆက်နွယ်မှုရှိပါက၊ ၎င်းတို့၏ ဆက်နွယ်မှုကို တွက်ချက်ရန် လေးထောင့်ဆုတ်ယုတ်မှုကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။

ဤကျူတိုရီရယ်တွင် R တွင် လေးပုံတပုံ ဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။

ဥပမာ- R တွင် လေးပုံတစ်ပုံ ဆုတ်ယုတ်မှု

အလုပ်လုပ်တဲ့ နာရီအရေအတွက်နဲ့ ပျော်ရွှင်မှုကို အစီရင်ခံတဲ့ကြားက ဆက်နွယ်မှုကို နားလည်ချင်တယ်ဆိုပါစို့။ ကျွန်ုပ်တို့တွင် တစ်ပတ်လျှင် အလုပ်လုပ်သည့် နာရီအရေအတွက်နှင့် ပတ်သက်သည့် အောက်ပါဒေတာနှင့် မတူညီသောလူ 11 ဦးအတွက် ပျော်ရွှင်မှုအဆင့် (0 မှ 100 အထိ) အစီရင်ခံတင်ပြသည်-

R တွင် လေးပုံတစ်ပုံ ဆုတ်ယုတ်မှုပုံစံကို အံဝင်ခွင်ကျဖြစ်စေရန် အောက်ပါအဆင့်များကို အသုံးပြုပါ။

အဆင့် 1: ဒေတာကိုထည့်ပါ။

ပထမဦးစွာ ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏ဒေတာများပါဝင်သော ဒေတာဘောင်တစ်ခုကို ဖန်တီးပါမည်။

 #createdata
data <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                   happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))

#viewdata 
data

   hours happiness
1 6 14
2 9 28
3 12 50
4 14 70
5 30 89
6 35 94
7 40 90
8 47 75
9 51 59
10 55 44
11 60 27

အဆင့် 2- ဒေတာကို မြင်ယောင်ကြည့်ပါ။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် ဒေတာကို မြင်ယောင်နိုင်ရန် ရိုးရှင်းသော အပိုင်းအစတစ်ခုကို ဖန်တီးပါမည်။

 #create scatterplot
plot(data$hours, data$happiness, pch=16) 

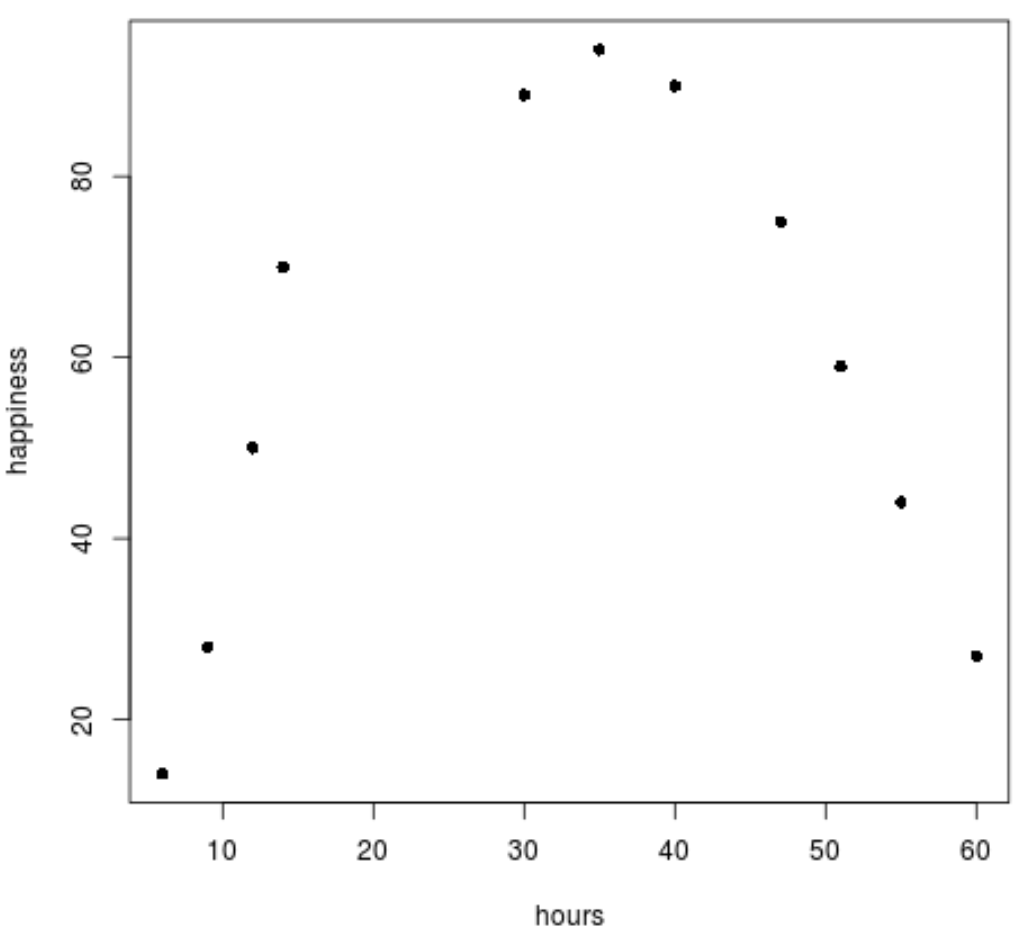
ဒေတာသည် linear ပုံစံအတိုင်း မလိုက်နာကြောင်း ရှင်းရှင်းလင်းလင်း သိမြင်နိုင်ပါသည်။

အဆင့် 3- ရိုးရှင်းသော linear regression model ကို ကိုက်ညီပါ။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် ဒေတာနှင့် မည်မျှ လိုက်ဖက်သည်ကို ကြည့်ရန် ရိုးရှင်းသော မျဉ်းကြောင်းအတိုင်း ဆုတ်ယုတ်မှု မော်ဒယ်ကို တပ်ဆင်ပါမည်။

 #fit linear model
linearModel <- lm(happiness ~ hours, data=data)

#view model summary
summary(linearModel)

Call:
lm(formula = happiness ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-39.34 -21.99 -2.03 23.50 35.11 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept) 48.4531 17.3288 2.796 0.0208 *
hours 0.2981 0.4599 0.648 0.5331  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 28.72 on 9 degrees of freedom
Multiple R-squared: 0.0446, Adjusted R-squared: -0.06156 
F-statistic: 0.4201 on 1 and 9 DF, p-value: 0.5331

မော်ဒယ်မှရှင်းပြထားသော ပျော်ရွှင်မှုစုစုပေါင်းကွဲလွဲမှုသည် 4.46% သာရှိပြီး၊ မျိုးစုံ R-squared တန်ဖိုးဖြင့်ပြသထားသည်။

အဆင့် 4- လေးပုံတစ်ပုံ ဆုတ်ယုတ်မှုပုံစံကို ကွက်တိပါ။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် လေးထောင့်ပုံသဏ္ဍာန် ဆုတ်ယုတ်မှုပုံစံနှင့် ကိုက်ညီပါမည်။

 #create a new variable for hours 2
data$hours2 <- data$hours^2

#fit quadratic regression model
quadraticModel <- lm(happiness ~ hours + hours2, data=data)

#view model summary
summary(quadraticModel)

Call:
lm(formula = happiness ~ hours + hours2, data = data)

Residuals:
    Min 1Q Median 3Q Max 
-6.2484 -3.7429 -0.1812 1.1464 13.6678 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.218 on 8 degrees of freedom
Multiple R-squared: 0.9602, Adjusted R-squared: 0.9502 
F-statistic: 96.49 on 2 and 8 DF, p-value: 2.51e-06

နမူနာပုံစံဖြင့် ရှင်းပြထားသော ပျော်ရွှင်မှု စုစုပေါင်းကွဲလွဲမှုသည် 96.02% အထိ တိုးလာသည်။

မော်ဒယ်သည် ဒေတာနှင့် မည်မျှကိုက်ညီကြောင်း မြင်သာစေရန် အောက်ပါကုဒ်ကို အသုံးပြုနိုင်ပါသည်။

 #create sequence of hour values
hourValues <- seq(0, 60, 0.1)

#create list of predicted happiness levels using quadratic model
happinessPredict <- predict(quadraticModel, list(hours=hourValues, hours2=hourValues^2))

#create scatterplot of original data values
plot(data$hours, data$happiness, pch=16)
#add predicted lines based on quadratic regression model
lines(hourValues, happinessPredict, col='blue')

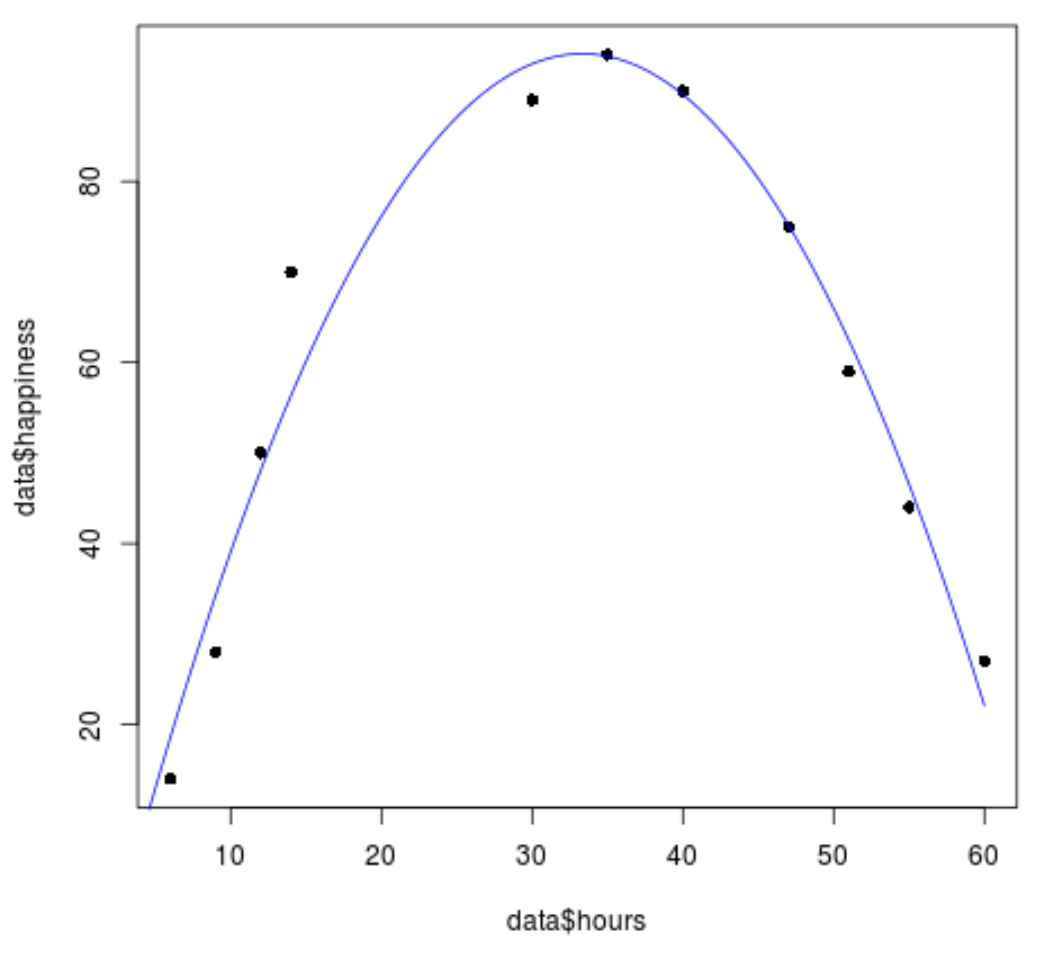
quadratic regression line သည် data values များနှင့် အတော်လေး ကိုက်ညီကြောင်း တွေ့နိုင်ပါသည်။

အဆင့် 5- လေးထောင့်ပုံစံ ဆုတ်ယုတ်မှုပုံစံကို အဓိပါယ်ဖွင့်ဆိုပါ။

ယခင်အဆင့်တွင်၊ Quadratic regression model ၏ရလဒ်မှာ-

 Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***

ဤနေရာတွင် တင်ပြထားသော ကိန်းဂဏန်းများအပေါ် အခြေခံ၍ ချိန်ညှိထားသော လေးထောင့်ပုံသဏ္ဍန်ဆုတ်ယုတ်မှုသည်-

ပျော်ရွှင်မှု = -0.1012 (နာရီ) ² + 6.7444 (နာရီ) – 18.2536

တစ်ပတ်လျှင် အလုပ်လုပ်သည့် နာရီအရေအတွက်ဖြင့် လူတစ်ဦးချင်းစီ၏ ခန့်မှန်းထားသော ပျော်ရွှင်မှုကို ရှာဖွေရန် ဤညီမျှခြင်းအား ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည်။

ဥပမာအားဖြင့်၊ တစ်ပတ်လျှင် နာရီ 60 အလုပ်လုပ်သူသည် ပျော်ရွှင်မှုအဆင့် 22.09 ရှိလိမ့်မည် ။

ပျော်ရွှင်မှု = -0.1012(60) ² + 6.7444(60) – 18.2536 = 22.09

အပြန်အလှန်အားဖြင့် တစ်ပတ်လျှင် နာရီ 30 အလုပ်လုပ်သူသည် ပျော်ရွှင်မှုအဆင့် 92.99 ရှိသင့်သည် ။

ပျော်ရွှင်မှု = -0.1012(30) ² + 6.7444(30) – 18.2536 = 92.99