Excel တွင် ယူနီဖောင်းဖြန့်ချီနည်းကို အသုံးပြုနည်း

တူညီသောဖြန့်ဝေမှုသည် a မှ b ကြားကာလတစ်ခုကြားရှိ တန်ဖိုးတစ်ခုစီတွင် ရွေးချယ်ခံရနိုင်ခြေတူညီသော ဖြစ်နိုင်ခြေဖြန့်ဝေမှုတစ်ခုဖြစ်သည်။

a မှ b ကြားကာလတစ်ခုတွင် x ₁ နှင့် x ₂ ကြားတန်ဖိုးတစ်ခုရရှိရန် ဖြစ်နိုင်ခြေကို ဖော်မြူလာကို အသုံးပြု၍ ရှာတွေ့နိုင်သည်-

P(x ₁ နှင့် x ₂ ကြားတန်ဖိုးကိုရယူပါ) = (x ₂ – x ₁ ) / (b – a)

ယူနီဖောင်း ဖြန့်ဖြူးမှုတွင် အောက်ပါ ဂုဏ်သတ္တိများ ရှိသည်။

• ဖြန့်ဖြူးမှု၏ ဆိုလိုရင်းမှာ μ = (a + b) / 2 ဖြစ်သည်။
• ဖြန့်ဖြူးမှု၏ကွဲလွဲမှုသည် σ ² = (b – a) ^2/12 ဖြစ်သည်။
• ဖြန့်ဖြူးမှု၏စံသွေဖည်မှုမှာ σ = √σ ² ဖြစ်သည်။

အောက်ဖော်ပြပါ ဥပမာများသည် Excel တွင် တူညီသော ဖြန့်ဝေမှုများ၏ ဖြစ်နိုင်ခြေများကို တွက်ချက်နည်းကို ပြသထားသည်။

မှတ်ချက်- Uniform Distribution Calculator ကို အသုံးပြု၍ အောက်ပါ ဥပမာတစ်ခုစီအတွက် ဖြေရှင်းချက်ကို သင်စစ်ဆေးနိုင်ပါသည်။

ဥပမာများ- Excel တွင် Uniform Distribution

ဥပမာ 1- ဘတ်စ်ကားသည် မိနစ် 20 တိုင်း ဘတ်စ်ကားမှတ်တိုင်သို့ ရောက်သည်။ ဘတ်စ်ကားမှတ်တိုင်ကိုရောက်ရင် 8 မိနစ်အတွင်း ဒါမှမဟုတ် ဒီထက်နည်းတဲ့ ဘတ်စ်ကားရောက်လာဖို့ ဖြစ်နိုင်ခြေဘယ်လောက်ရှိလဲ။

ဖြေရှင်းချက်-

• a: 0 မိနစ်
• B: 20 မိနစ်
• x ₁ : 0 မိနစ်
• _x2 : 8 မိနစ်

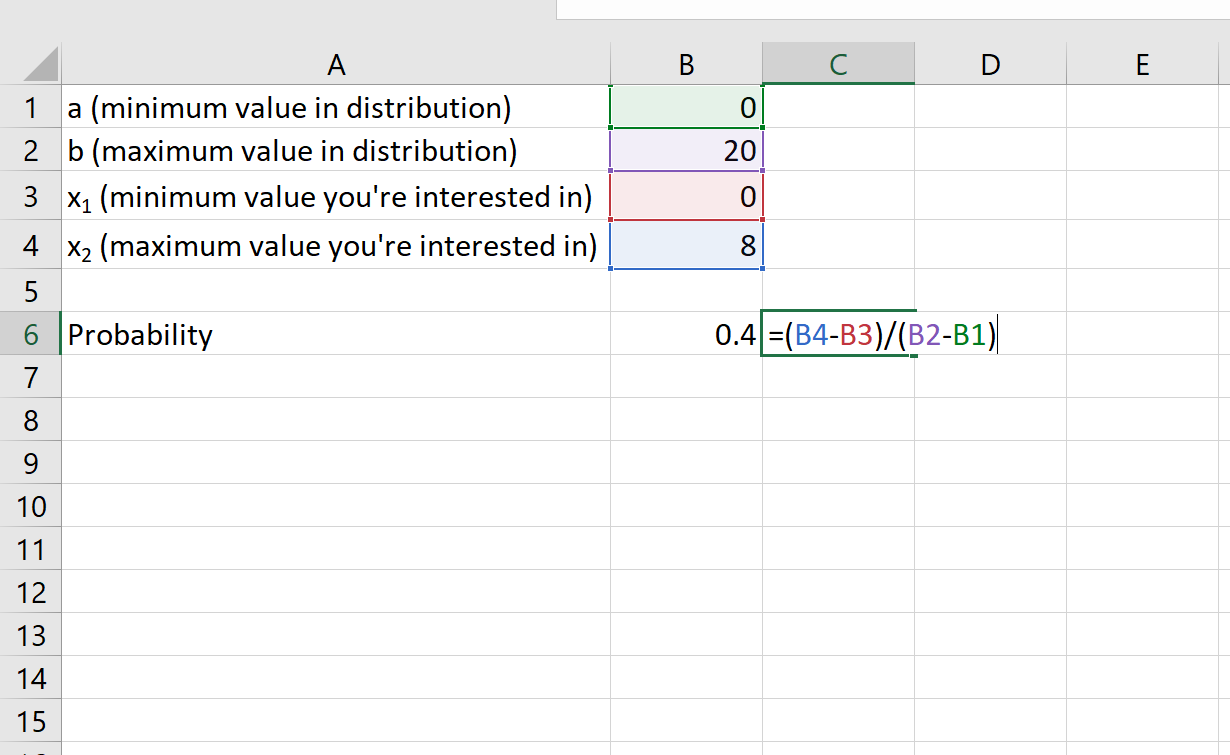
ဘတ်စ်ကားသည် 8 မိနစ် သို့မဟုတ် ထို့ထက်နည်းသော ဘတ်စကား ရောက်ရှိလာမည့် ဖြစ်နိုင်ခြေမှာ 0.4 ဖြစ်သည်။

ဥပမာ 2- အချို့ဖားမျိုးစိတ်များ၏ အလေးချိန်သည် 15 မှ 25 ဂရမ်ကြား အညီအမျှခွဲဝေပါသည်။ ဖားတစ်ကောင်ကို ကြုံသလိုရွေးရင် အလေးချိန် 17 ဂရမ်ကနေ 19 ဂရမ်ကြား ဖြစ်နိုင်ခြေဘယ်လောက်ရှိလဲ။

ဖြေရှင်းချက်-

• a: 15 ဂရမ်
• b: 25 ဂရမ်
• x ₁ : 17 ဂရမ်
• x ₂ : 19 ဂရမ်

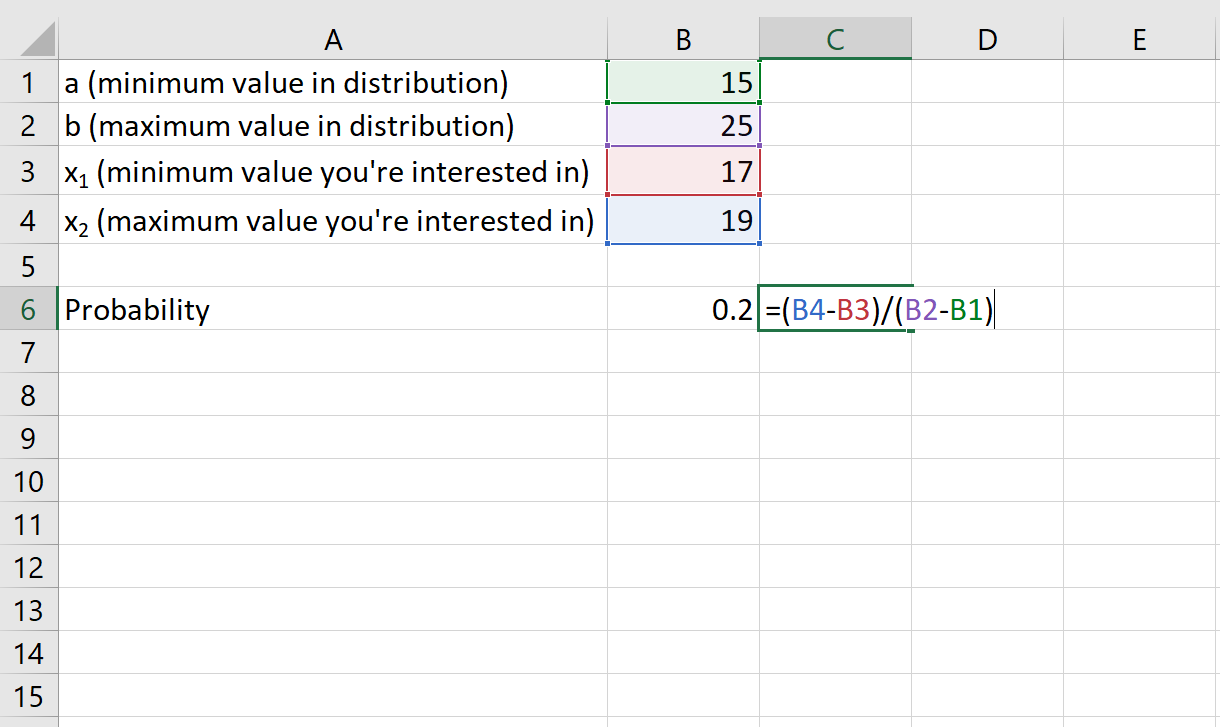
ဖားအလေးချိန် ၁၇ ဂရမ်မှ ၁၉ ဂရမ်ကြား ဖြစ်နိုင်ခြေမှာ ၀.၂ ဖြစ်သည်။

ဥပမာ 3- NBA ဂိမ်းတစ်ခု၏ကြာချိန်သည် မိနစ် 120 နှင့် 170 ကြားတွင် အညီအမျှ ဖြန့်ဝေသည်။ ကျပန်းရွေးချယ်ထားသော NBA ဂိမ်းသည် မိနစ် 150 ကျော်ကြာနိုင်ခြေ မည်မျှရှိသနည်း။

ဖြေရှင်းချက်-

• တစ်ခု : 120 မိနစ်
• B: 170 မိနစ်
• x ₁ : 150 မိနစ်
• _x2 : ၁၇၀ မိနစ်

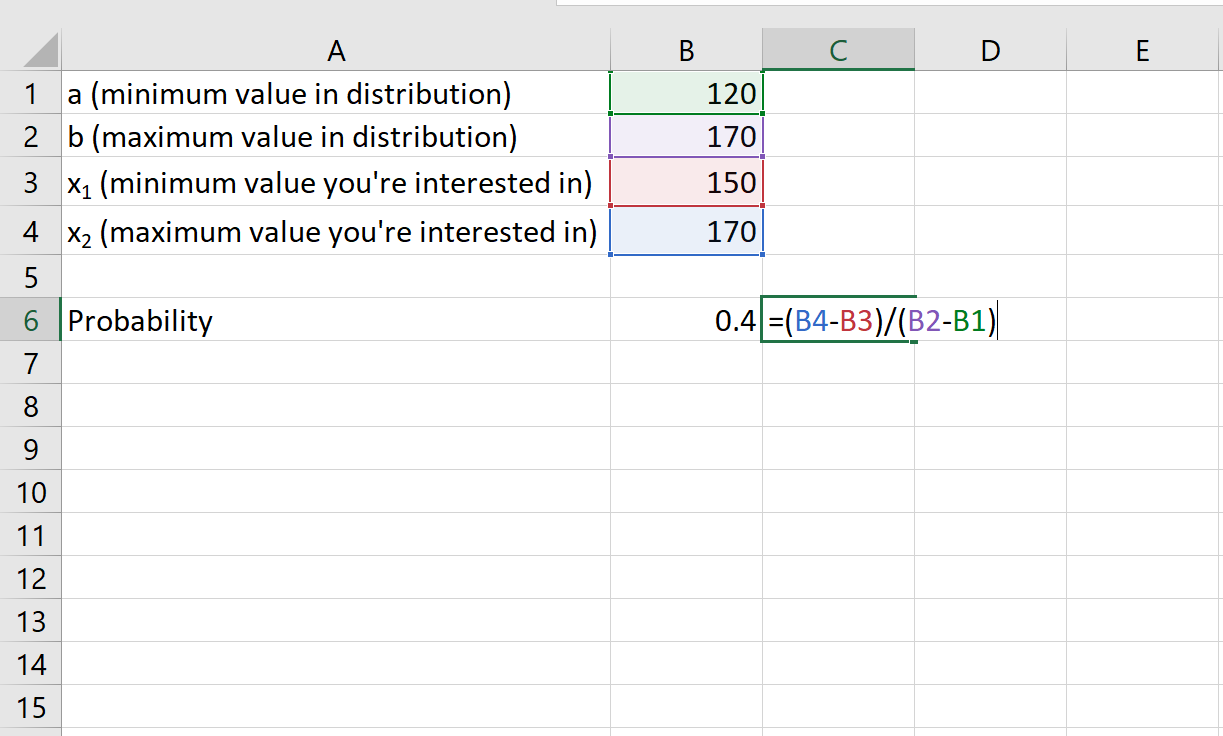
ကျပန်းရွေးချယ်ထားသော NBA ဂိမ်းသည် မိနစ် 150 ကျော်ကြာနိုင်ခြေသည် 0.4 ဖြစ်သည်။

ဤစာမျက်နှာတွင် နောက်ထပ် Excel သင်ခန်းစာများကို ရှာဖွေပါ။