Density curves ဆိုတာ ဘာလဲ။ (ရှင်းလင်းချက်နှင့် ဥပမာများ)

သိပ်သည်းဆမျဉ်းကွေး ဆိုသည်မှာ ဒေတာအစုတစ်ခုအတွင်း တန်ဖိုးများ ဖြန့်ဖြူးခြင်းကို ကိုယ်စားပြုသော ဂရပ်တစ်ခုပေါ်ရှိ မျဉ်းကွေးတစ်ခုဖြစ်သည်။ ၎င်းသည် အကြောင်းပြချက်သုံးခုအတွက် အသုံးဝင်သည်-

1. သိပ်သည်းမှုမျဉ်းကွေးတစ်ခုသည် ဖြန့်ဖြူးမှုတစ်ခုတွင် ကြိမ်နှုန်းတန်ဖိုးများ တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော “ အထွတ်အထိပ်များ” ရှိ၊ မရှိ အပါအဝင် ဖြန့်ဖြူးမှုတစ်ခု၏ “ ပုံသဏ္ဍာန်” ကို ကောင်းမွန်သော အကြံဥာဏ်ပေးသည်။ ဒါမှမဟုတ် မှန်တယ်။ ညာဘက်။ .

2. သိပ်သည်းဆမျဉ်းကွေးသည် ဖြန့်ဖြူးမှုတစ်ခု၏ ပျမ်းမျှနှင့် အလယ်တန်း ဆက်စပ်နေသည့်နေရာကို အမြင်အာရုံဖြင့် မြင်နိုင်စေပါသည်။

3. သိပ်သည်းမှုမျဉ်းကွေးတစ်ခုသည် မတူညီသောတန်ဖိုးများကြားတွင် ဒေတာအစုတစ်ခုအတွင်း စူးစမ်းလေ့လာမှုရာခိုင်နှုန်းမည်မျှရှိသည်ကို မြင်သာစွာမြင်နိုင်စေပါသည်။

လူသိအများဆုံး သိပ်သည်းဆမျဉ်းကွေးမှာ ပုံမှန်ဖြန့်ဖြူးမှုကို ကိုယ်စားပြုသည့် ခေါင်းလောင်းပုံစံမျဉ်းကွေးဖြစ်သည်။

သိပ်သည်းဆ မျဉ်းကွေးများကို ပိုမိုကောင်းမွန်စွာ နားလည်ရန် အောက်ပါ ဥပမာကို သုံးသပ်ကြည့်ပါ။

ဥပမာ- သိပ်သည်းဆမျဉ်းကွေးကို ဖန်တီးခြင်းနှင့် အဓိပ္ပာယ်ပြန်ဆိုခြင်း။

နယ်ပယ်တစ်ခုတွင် မတူညီသောအပင် 20 (လက်မဖြင့်) အမြင့်ကိုပြသသည့် အောက်ပါဒေတာအတွဲရှိသည် ဆိုကြပါစို့။

၄၊ ၅၊ ၅၊ ၆၊ ၆၊ ၆၊ ၆၊ ၇၊ ၇၊ ၇၊ ၇၊ ၇၊ ၇၊ ၈၊ ၈၊ ၈၊ ၉၊ ၉၊ ၉၊ ၂၊

အကယ်၍ ကျွန်ုပ်တို့သည် တန်ဖိုးတစ်ခုစီ၏ နှိုင်းရကြိမ်နှုန်းများကို ပြသရန် ရိုးရှင်းသော ဟီစတိုဂရမ်တစ်ခုကို ဖန်တီးပါက၊ ၎င်းသည် ဤကဲ့သို့ ဖြစ်လိမ့်မည်-

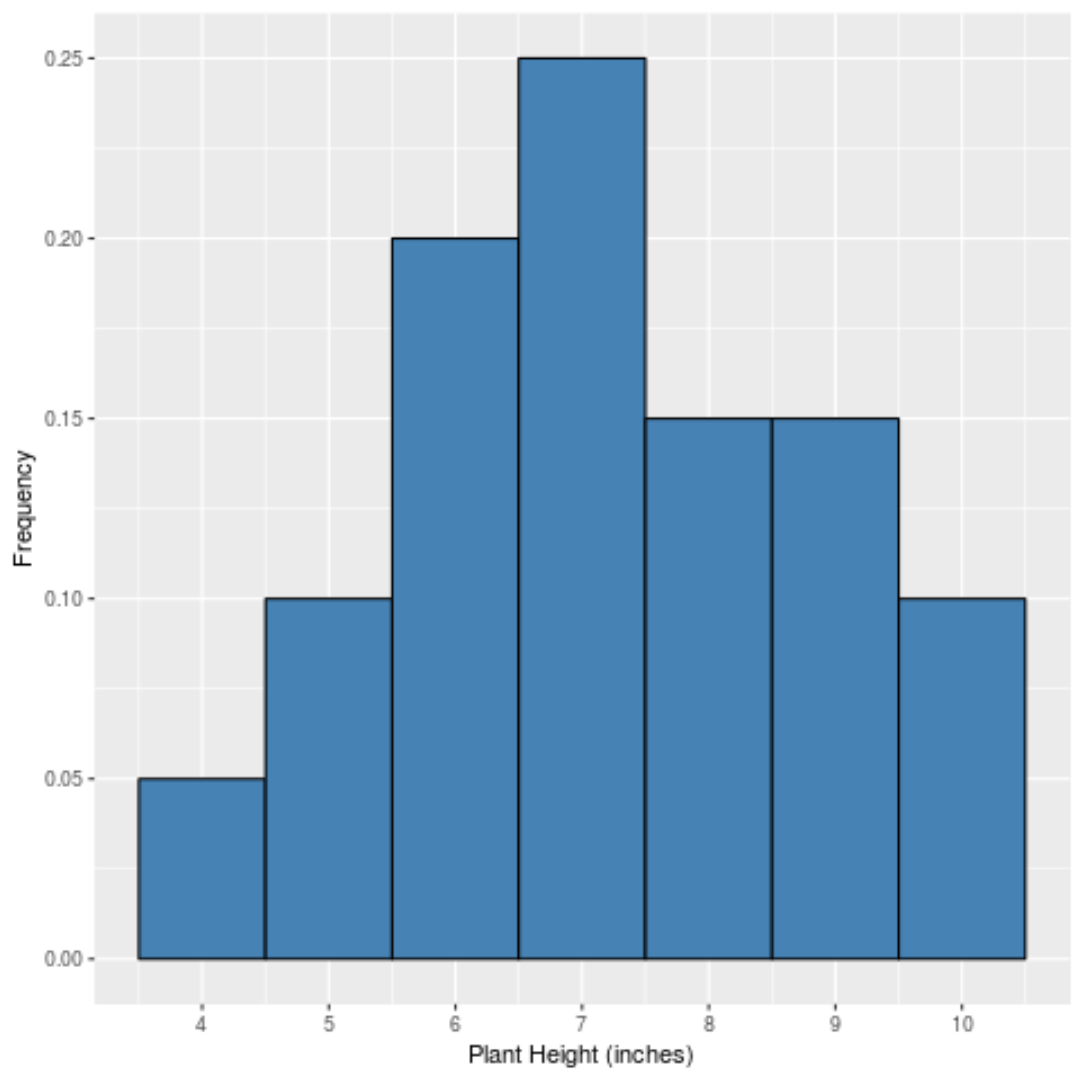
x-axis သည် ဒေတာတန်ဖိုးကိုပြသပြီး y-axis သည် နှိုင်းရကြိမ်နှုန်းကိုပြသသည် (ဥပမာ၊ တန်ဖိုး “ 7” သည် dataset ရှိ စုစုပေါင်းတန်ဖိုး 20 တွင် 5 ဆ ပေါ်လာသည်၊ ထို့ကြောင့် ၎င်းတွင် နှိုင်းရကြိမ်နှုန်း 25% သို့မဟုတ်၊ ၀.၂၅ ။

အကယ်၍ ကျွန်ုပ်တို့သည် ဤဖြန့်ဖြူးမှု၏ “ ပုံသဏ္ဍာန်” ကိုဖမ်းယူရန် သိပ်သည်းဆမျဉ်းကွေး တစ်ခုကို ဖန်တီးပါက၊ ၎င်းသည် ဤကဲ့သို့ဖြစ်လိမ့်မည်-

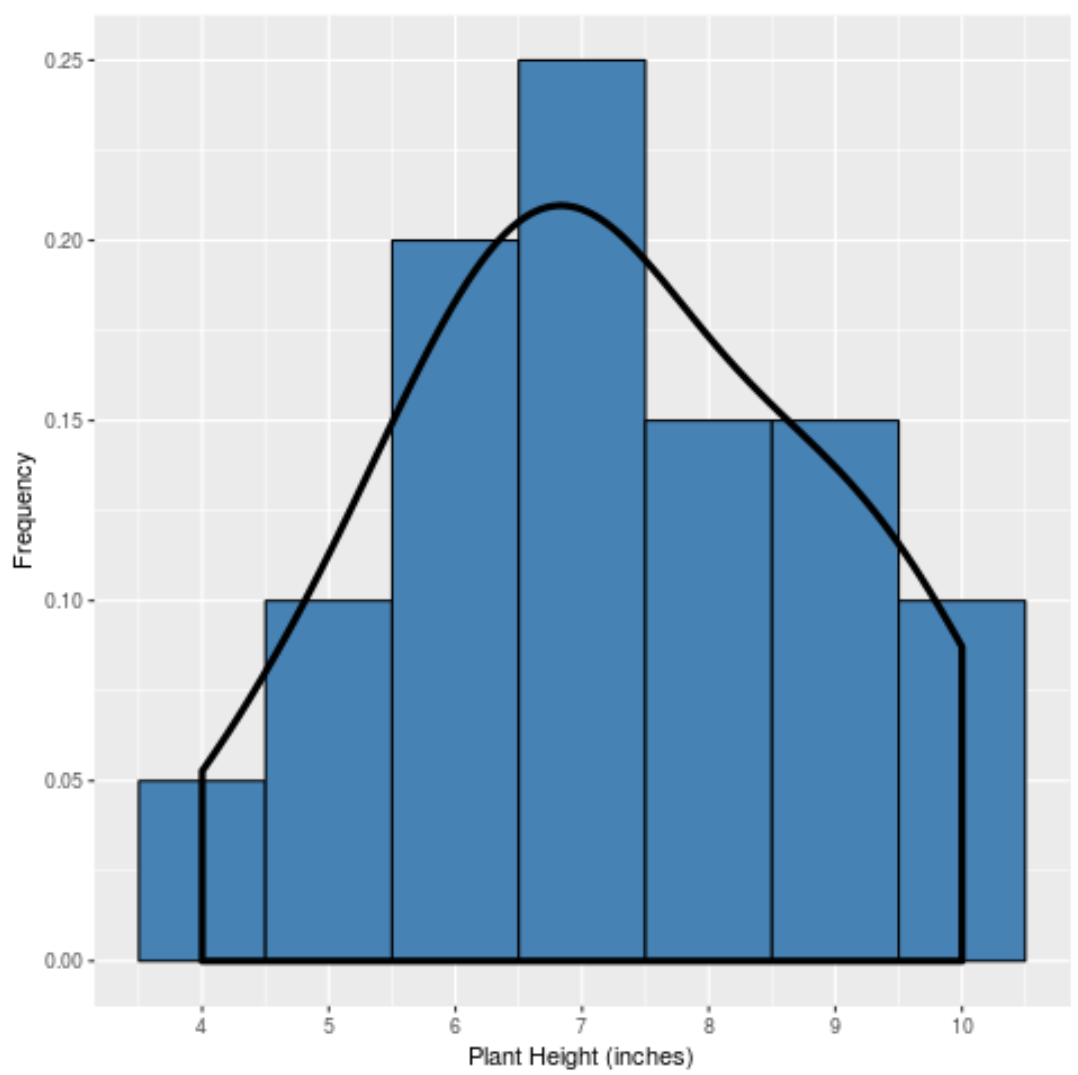
မျဉ်းကွေးသည် ဖြန့်ဖြူးမှု၏ဗဟိုအနီးတွင် အမြင့်ဆုံးဖြစ်ပြီး ၎င်းသည် တန်ဖိုးအများစုကို တွေ့ရှိသည့်နေရာဖြစ်သည်။ အပင်အနည်းငယ်သည် ဤတန်ဖိုးများ (ဥပမာ အမြင့် 4 လက်မ သို့မဟုတ် 10 လက်မ) ဖြစ်သောကြောင့် ဖြန့်ဖြူးမှု၏အဆုံးအနီးတွင်လည်း အနိမ့်ဆုံးဖြစ်သည်။

သိပ်သည်းဆ မျဉ်းကွေးများ အဓိပ္ပာယ်ဖွင့်ဆိုပုံ

သိပ်သည်းမှု မျဉ်းကွေးများသည် ပုံသဏ္ဍာန်နှင့် အရွယ်အစား အားလုံးတွင် ပါ၀င်ပြီး ၎င်းတို့သည် ပေးထားသော ဒေတာအစုံတွင် တန်ဖိုးများ ဖြန့်ဖြူးခြင်းဆိုင်ရာ လျင်မြန်သော အမြင်အာရုံ နားလည်မှုကို ရရှိစေပါသည်။ ၎င်းတို့သည် ကျွန်ုပ်တို့ကို မြင်ယောင်နိုင်ရန် ကူညီပေးရာတွင် အထူးအသုံးဝင်သည်-

1. Asymmetry

Skewness သည် ဖြန့်ဖြူးမှုတစ်ခု၏ symmetry ကိုဖော်ပြသည့်နည်းလမ်းတစ်ခုဖြစ်သည်။ သိပ်သည်းမှု မျဉ်းကွေးများသည် ဂရပ်တစ်ခုအား ဘယ်၊ ညာ စောင်းခြင်း သို့မဟုတ် တိမ်းစောင်းခြင်းမရှိသည်ကို လျင်မြန်စွာ သိမြင်နိုင်စေသည်-

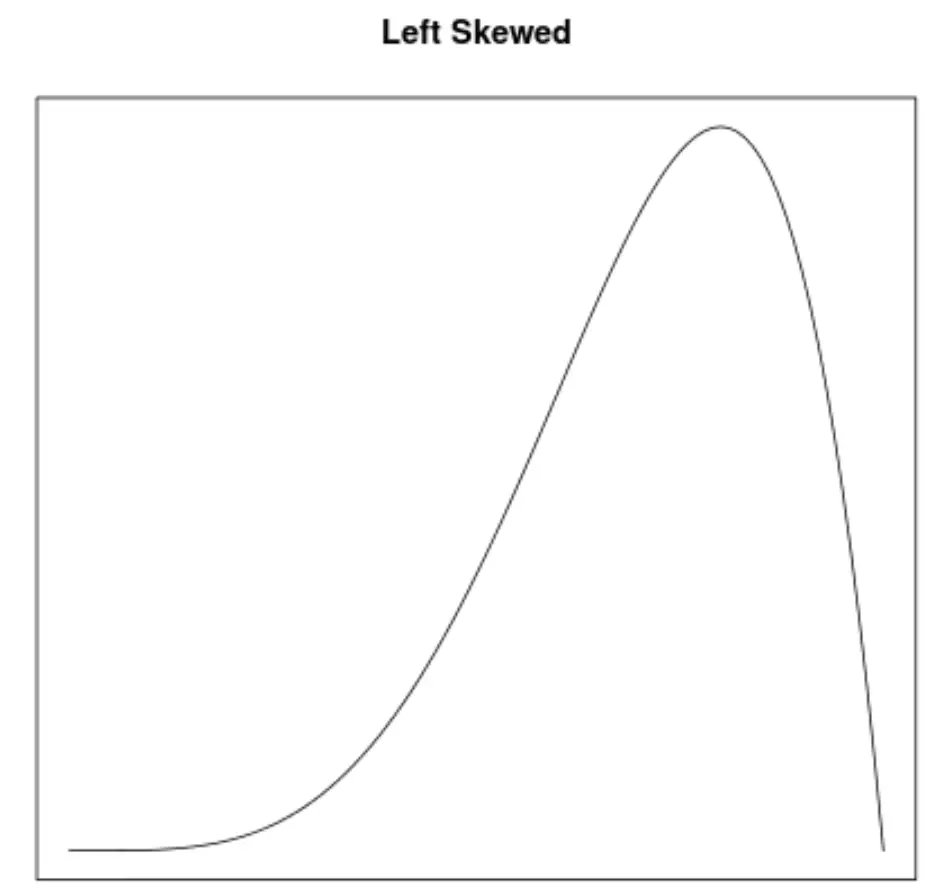
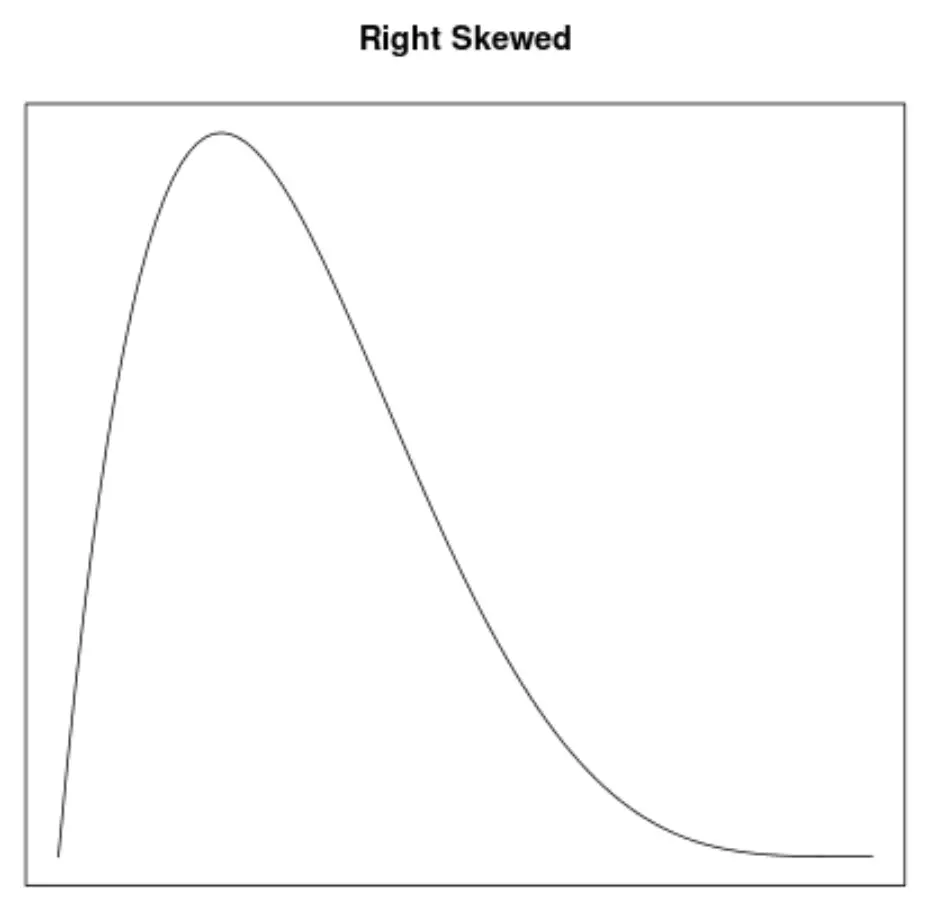
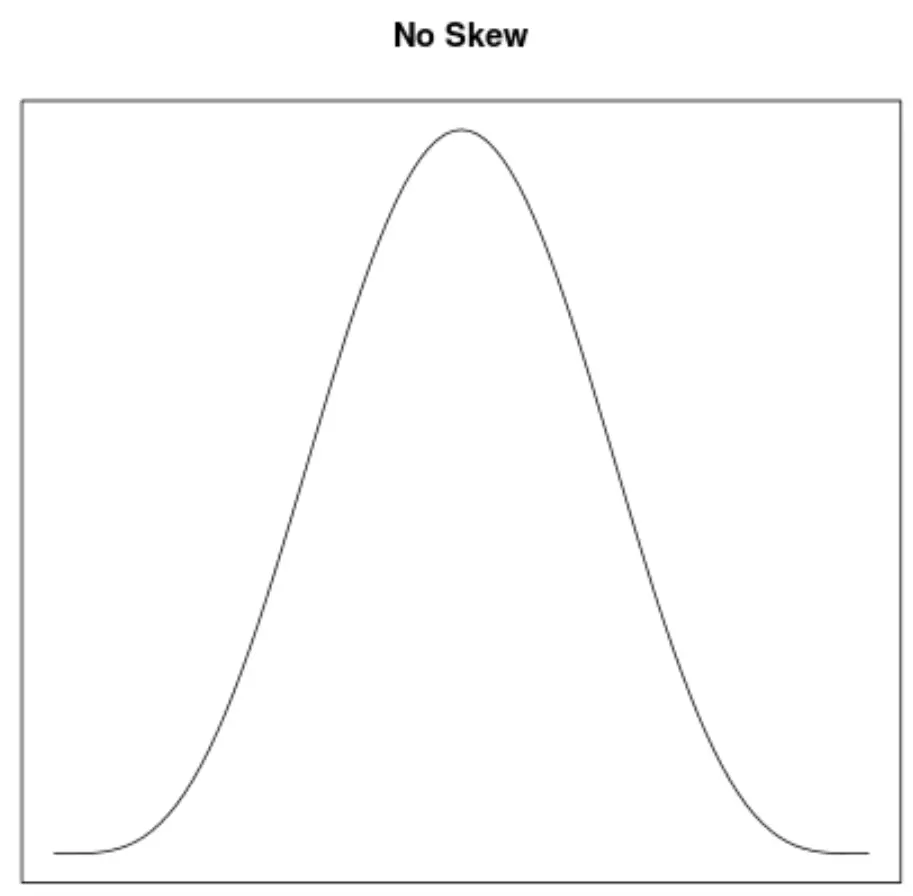
2. mean နှင့် median ၏တည်နေရာ

သိပ်သည်းဆမျဉ်းကွေး၏ ချို့ယွင်းချက်အပေါ် အခြေခံ၍ ပေးထားသော ဖြန့်ဖြူးမှုတစ်ခုတွင် ပျမ်းမျှ သို့မဟုတ် ပျမ်းမျှသည် ပိုကြီးခြင်းရှိမရှိ လျင်မြန်စွာ ပြောပြနိုင်သည်။ အထူးသဖြင့်-

• သိပ်သည်းဆမျဉ်းကွေးသည် အချိုးမညီဘဲ ဖြစ်နေ ပါက ပျမ်းမျှသည် ပျမ်းမျှထက် နိမ့်သည် ။
• density curve သည် ညာဘက်သို့ စောင်းနေ ပါက mean သည် median ထက် ကြီးပါသည် ။
• သိပ်သည်းဆမျဉ်းကွေးသည် အချိုးမညီ ပါက၊ ပျမ်းမျှသည် မီဒီယံနှင့် ညီမျှသည် ။

3. အထွတ်အထိပ်အရေအတွက်

သိပ်သည်းဆ မျဉ်းကွေးများသည် ပေးထားသော ဖြန့်ဖြူးမှုတစ်ခုတွင် “အထွတ်အထိပ်များ” မည်မျှရှိသည်ကို လျင်မြန်စွာ မြင်နိုင်စေပါသည်။ အထက်ဖော်ပြပါ ဥပမာတစ်ခုစီတွင်၊ ဖြန့်ဝေမှုများသည် အထွတ်အထိပ်တစ်ခုသာရှိသောကြောင့် ဤဖြန့်ဝေမှုများကို စံမညီသော အဖြစ်ဖြင့် ဖော်ပြပါမည်။

သို့သော်၊ အချို့သောဖြန့်ဝေမှုများတွင် ကျွန်ုပ်တို့ bimodal distributions ဟုခေါ်သော အထွတ်အထိပ်နှစ်ခုရှိနိုင်သည်။ ရှားပါးသောကိစ္စများတွင် ကျွန်ုပ်တို့သည် အထွတ်အထိပ်နှစ်ခု သို့မဟုတ် ထို့ထက်ပိုသော ဘက်စုံဖြန့် ဝေမှုများ လည်း ရှိနိုင်ပါသည်။

ပေးထားသော ဒေတာအတွဲတစ်ခုအတွက် သိပ်သည်းဆမျဉ်းကွေးတစ်ခုကို ဖန်တီးခြင်းဖြင့်၊ ဖြန့်ဝေမှုတွင် အမြင့်ဆုံးမည်မျှရှိသည်ကို ကျွန်ုပ်တို့ လျင်မြန်စွာ မြင်တွေ့နိုင်သည်။

သိပ်သည်းဆ မျဉ်းကွေးများ၏ ဂုဏ်သတ္တိများ

သိပ်သည်းဆ မျဉ်းကွေးများသည် အောက်ပါ ဂုဏ်သတ္တိများ ရှိသည်။

• မျဉ်းကွေးအောက်ရှိ ဧရိယာသည် အမြဲတမ်း 100% အထိ ပေါင်းပါသည်။
• မျဉ်းကွေးသည် x ဝင်ရိုးအောက် ဘယ်တော့မှ မသွားပါ။

မတူညီသောဖြန့်ဝေမှုအတွက် သိပ်သည်းဆမျဉ်းကွေးများ ဖန်တီးခြင်း သို့မဟုတ် အဓိပ္ပာယ်ဖွင့်ဆိုသည့်အခါ ဤအချက်နှစ်ခုကို သတိရပါ။

ထပ်လောင်းအရင်းအမြစ်များ

Relative Frequency Histograms မိတ်ဆက်
Excel တွင် Bell Curve ဖန်တီးနည်း
Python တွင် Bell Curve ဖန်တီးနည်း