Harmonic ပျမ်းမျှ

အားဖြင့် Benjamin Anderson ဩဂုတ် 6, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤတွင် ကျွန်ုပ်တို့သည် ဟာမိုနီဆိုလိုအား မည်ကဲ့သို့ တွက်ချက်ပုံ (ဖော်မြူလာ) ကို ရှင်းပြပါသည်။ ထို့အပြင်၊ ဥပမာတစ်ခု၏ ဟာမိုနီဆိုလိုအား အဆင့်ဆင့် တွက်ချက်ပါသည်။ မည်သည့်ဒေတာအတွဲ၏ ဟာမိုနီဆိုလိုချက်ကို ယူရန် ဂဏန်းပေါင်းစက်ကိုလည်း သင်တွေ့လိမ့်မည်။ နောက်ဆုံးအနေနဲ့၊ ဟာမိုနီဆိုလိုးရဲ့ ဂုဏ်သတ္တိတွေက ဘာတွေလဲဆိုတာ သင်မြင်နိုင်မှာပါ။

ဟာမိုနီဟူသည် အဘယ်နည်း။

ဟာမိုနီဆိုလိုသည်မှာ သရုပ်ဖော်ကိန်းဂဏန်းများ၏ ဗဟိုအနေအထားတိုင်းတာမှုဖြစ်သည်။ ဟာမိုနီဆိုလိုရင်းကို တန်ဖိုးတစ်ခုစီ၏ အပြန်အလှန်အကျိုးသက်ရောက်မှုများ၏ပေါင်းလဒ်ဖြင့် ကိန်းဂဏန်းအချက်အလက်စုစုပေါင်းအရေအတွက်ကို ပိုင်းခြားခြင်းဖြင့် တွက်ချက်သည်။

ပျမ်းမျှအမြန်နှုန်း၊ အချိန်များကို တွက်ချက်ရန် သို့မဟုတ် အီလက်ထရွန်နစ် တွက်ချက်မှုပြုလုပ်ရန် ဟာမိုနီပျမ်းမျှအား အသုံးပြုသည်။ ဤအင်္ဂါရပ်သည် ပျမ်းမျှစျေးနှုန်းများ သို့မဟုတ် ရာခိုင်နှုန်းများကို တွက်ချက်ရာတွင် မကြာခဏအသုံးပြုလေ့ရှိသည့် အခြားပျမ်းမျှအမျိုးအစားများနှင့် ဟာမိုနီပျမ်းမျှအား ကွဲပြားစေသည်။

ထို့ကြောင့်၊ harmonic mean အတွက် ပုံသေနည်းမှာ အောက်ပါအတိုင်းဖြစ်သည်။

ဟာမိုနီပျမ်းမျှအား အများအားဖြင့် မြို့တော် H ဖြင့် ကိုယ်စားပြုသည်။

ကျန်ရှိသောပျမ်းမျှအမျိုးအစားများမှာ ဂဏန်းသင်္ချာပျမ်းမျှ၊ အလေးချိန်ပျမ်းမျှ၊ စတုရန်းပျမ်းမျှနှင့် ဂျီဩမေတြီပျမ်းမျှတို့ဖြစ်သည်။ Harmonic ပျမ်းမျှသည် အခြားပျမ်းမျှအမျိုးအစားများနှင့် နှိုင်းယှဉ်ပါက အားသာချက်များနှင့် အားနည်းချက်များရှိသည်၊ ၎င်းတို့သည် အဘယ်အရာဖြစ်သည်ကို အောက်တွင်ဖော်ပြထားသည်။

Harmonic Mean တွက်နည်း

ဟာမိုနီဆိုလိုအား တွက်ချက်ရန်အတွက် အောက်ပါအဆင့်များကို လုပ်ဆောင်ရပါမည်-

နမူနာရှိ စာရင်းအင်းဒေတာတစ်ခုစီ၏ ပြောင်းပြန်ကို တွက်ချက်ပါ။
တွက်ချက်ထားသော ပြောင်းပြန်များအားလုံးကို ထည့်ပါ။
ယခင်အဆင့်တွင်တွေ့ရသော ပေါင်းလဒ်ဖြင့် ဒေတာစုစုပေါင်းအရေအတွက်ကို ပိုင်းခြားပါ။
ရရှိသောရလဒ်မှာ ကိန်းဂဏန်းနမူနာ၏ ဟာမိုနီဆိုလိုရင်းဖြစ်သည်။

👉 သင်တွေ့မြင်ရသည့်အတိုင်း data set တစ်ခု၏ harmonic mean ကိုရယူရန် လည်ပတ်မှုများစွာလိုအပ်သောကြောင့် ၎င်းကိုလက်ဖြင့်ပြုလုပ်ရန် အလွန်ပင်ပန်းပါသည်။ ထို့ကြောင့်၊ harmonic mean ကို တွက်ချက်ရန်၊ အောက်ပါ calculator ကို အသုံးပြုရန် အကြံပြုအပ်ပါသည်။

Harmony ၏ ဥပမာ

ဟာမိုနီဆိုလိုရင်းဆိုင်ရာ သီအိုရီကို ကြည့်ပြီးနောက်၊ စတော့ရှယ်ယာတစ်ခု၏စျေးနှုန်းနမူနာကို တစ်ဆင့်ပြီးတစ်ဆင့် ဖြေရှင်းခြင်းဖြင့် ဒေတာအစုတစ်ခု၏ ဟာမိုနီဆိုလိုကို မည်သို့ရှာဖွေရမည်နည်း။

လူတစ်ဦးသည် ကုမ္ပဏီတစ်ခု၏ အစုရှယ်ယာများကို နှစ်စဉ် ၅ နှစ်ဆက်တိုက် ဝယ်ယူသည်။ ဤကာလအတွင်း အစုရှယ်ယာများ၏စျေးနှုန်းသည် များစွာအတက်အကျဖြစ်သည်- ပထမနှစ်တွင် ရှယ်ယာတစ်ခုစီသည် ယူရို ၇ ယူရို၊ ဒုတိယနှစ်တွင် ၁၀ ယူရို၊ တတိယနှစ်တွင် ၁၅ ယူရို၊ စတုတ္ထနှစ်တွင် ကုမ္ပဏီသည် သိသိသာသာ ငွေကြေးဆုံးရှုံးမှုများနှင့် ကြုံတွေ့ခဲ့ရပါသည်။ စျေးနှုန်းသည် ရှယ်ယာတစ်ခုလျှင် ယူရို ၆ သို့ ကျဆင်းသွားပြီး နောက်ဆုံးတွင်၊ ပဉ္စမနှစ်တွင် ကုမ္ပဏီသည် စျေးနှုန်းကို ယူရို ၁၁ အထိ တိုးစေသည့် ကြီးမားသော ရင်းနှီးမြှုပ်နှံမှုတစ်ခုကို ပြုလုပ်ခဲ့သည်။ ရှယ်ယာများ၏ ပျမ်းမျှဝယ်ယူမှုစျေးနှုန်းက ဘယ်လောက်လဲ။

ရွေးချယ်စရာတစ်ခုမှာ ဂဏန်းသင်္ချာပျှမ်းမျှကို တွက်ချက်ရန်ဖြစ်ပြီး၊ ဆိုလိုသည်မှာ၊ စျေးနှုန်းများအားလုံးကို ပေါင်းထည့်ကာ ၎င်းတို့ကို ငါးခုဖြင့် ပိုင်းခြားခြင်းဖြစ်သည်။ သို့ရာတွင်၊ ဝယ်ယူမှုများသည် မတူညီသောနှစ်များအတွင်း ပြုလုပ်ခဲ့သောကြောင့်၊ ဂဏန်းသင်္ချာပျှမ်းမျှကို ရယူခြင်းသည် အမှားအယွင်းတစ်ခုဖြစ်သည်။ ထို့ကြောင့် ကျွန်ုပ်တို့သည် ဈေးနှုန်းအားလုံး၏ ဟာမိုနီဆိုလိုရင်းကို ရှာဖွေရပါမည်။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် ဟာမိုနီ ပျမ်းမျှဖော်မြူလာကို ကျင့်သုံးသည်-

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}+\frac{1}{x_4}+\frac{1}{x_5}}$

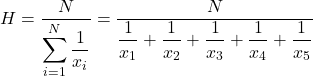
ထို့နောက် ကျွန်ုပ်တို့သည် ပြဿနာရှိသော စျေးနှုန်းတန်ဖိုးများကို ဖော်မြူလာတွင် အစားထိုးပြီး ဟာမိုနီဆိုလိုအား တွက်ချက်သည်-

$\displaystyle H=\frac{5}{\displaystyle\frac{1}{7}+\frac{1}{10}+\frac{1}{15}+\frac{1}{6}+\frac{1}{11}}=8,82$

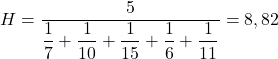
အချက်အလက်ငါးခုရှိသောကြောင့် အပိုင်းပိုင်း၏ပိုင်းဝေတွင် ငါးခုထည့်ရပါမည်။

ထို့ကြောင့်၊ ဤကာလအတွင်း သင်ဝယ်ယူထားသော ရှယ်ယာများ၏ ပျမ်းမျှစျေးနှုန်းသည် ရှယ်ယာတစ်ခုလျှင် 8.82 ယူရိုဖြစ်သည်။

Harmonic Mean ဂဏန်းတွက်စက်

အောက်ဖော်ပြပါ ဂဏန်းပေါင်းစက်ဖြင့် သင်သည် မည်သည့် ကိန်းဂဏန်း အချက်အလက်အစုံ၏ ဟာမိုနီပျမ်းမျှကို တွက်ချက်နိုင်သည်။

ဒဿမခွဲထွက်ကိရိယာအဖြစ် အစက်ကို အသုံးပြု၍ နံပါတ်များကို ထည့်သွင်းပြီး နံပါတ်များကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားရပါမည်။ ဟာမိုနီဆိုလိုရင်းကို ရှာရန်၊ မည်သည့်တန်ဖိုးမှ သုညမဖြစ်နိုင်ကြောင်း သတိရပါ။

ဟာမိုနီ၏ ဂုဏ်သတ္တိများကို ဆိုလိုသည်။

ဟာမိုနီဆိုလိုရင်းတွင် အောက်ပါလက္ခဏာများရှိသည်။

ကြီးမားသော တန်ဖိုးများသည် အစုအဖွဲ့တစ်ခု၏ ဟာမိုနီဆိုလိုအပေါ် အနည်းငယ်သာ သက်ရောက်မှုရှိသည်၊ ဆိုလိုသည်မှာ အခြားဒေတာနှင့် နှိုင်းယှဉ်ပါက အလွန်ကြီးမားသော တန်ဖိုးသည် ဟာမိုနီဆိုလိုအားတွင် သိသာထင်ရှားသော အပြောင်းအလဲကို ဖြစ်စေမည်မဟုတ်ပါ။

အခြားတစ်ဖက်တွင်၊ သေးငယ်သောတန်ဖိုးသည် အစုအဖွဲ့တစ်ခု၏ ဟာမိုနီဆိုလိုအားကို များစွာလွှမ်းမိုးစေပြီး ၎င်း၏တန်ဖိုးကို သိသိသာသာ လျော့ကျစေသည်။ အမှန်မှာ၊ ဖော်မြူလာ၏ ပိုင်းခြေ၏ အပြန်အလှန်အကျိုးဆက်များသည် အလွန်ကြီးမားသော တန်ဖိုးများကို ယူသည်။

ဖော်မြူလာတွင် မဆုံးဖြတ်နိုင်ခြင်းကြောင့် ဒေတာများထဲမှ သုညဖြစ်လျှင် ဟာမိုနီဆိုလိုအား တွက်ချက်မရနိုင်ပါ။ ထိုသို့သော အခြေအနေမျိုးတွင်၊ ဟာမိုနီဆိုလိုအား အဓိပ္ပါယ်မရှိဟု ဆိုပါသည်။

ဟာမိုနီဆိုလိုရင်း၏အပြန်အလှန်သည် လေ့လာသုံးသပ်ချက်များ၏ အပြန်အလှန်ဂဏန်းသင်္ချာဆိုလိုနှင့် ညီမျှသည်။

တူညီသောဒေတာအုပ်စုအတွက်၊ ဟာမိုနီဆိုလိုသည် ဂဏန်းသင်္ချာပျမ်းမျှထက်နည်းသည် သို့မဟုတ် ညီမျှမည်ဖြစ်သည်။

$\cfrac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}\leq \cfrac{x_1+x_2+\dots+x_N}{N}$

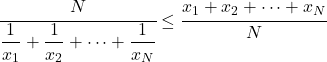
ဟာမိုနီကို Excel ဖြင့် တွက်ချက်ပါ။

ကျွန်ုပ်တို့မြင်ခဲ့ရသည့်အတိုင်း၊ တွက်ချက်မှုများစွာကို လုပ်ဆောင်ရန် လိုအပ်သောကြောင့် ဟာမိုနီကို ကိုယ်တိုင် တွက်ချက်ခြင်းသည် အလွန်ပျင်းစရာကောင်းပါသည်။ ပြီးတော့ သင့်မှာ ဒေတာပမာဏအများကြီးရှိတဲ့အခါ ပိုရှုပ်ထွေးလာမယ်။ ထို့ကြောင့်၊ harmonic mean ကိုရှာရန်၊ ဂဏန်းပေါင်းစက် သို့မဟုတ် Excel ပရိုဂရမ်ကို အသုံးပြုရန် အကြံပြုအပ်ပါသည်။

Excel ရှိ သဟဇာတ ပျမ်းမျှအား MEAN.ARMO ဖော်မြူလာဖြင့် တွက်ချက်သည်။ ဆိုလိုသည်မှာ၊ ဒေတာအစုတစ်ခု၏ သဟဇာတဖြစ်နှုန်းကို တွက်ချက်ရန်၊ ၎င်းတို့ကို Excel စာရွက်တစ်ခုသို့ ကူးယူပြီး MEAN.ARMO လုပ်ဆောင်ချက်ထဲသို့ ဒေတာအားလုံးကို ထည့်သွင်းရန် လိုအပ်သည်။

ဥပမာအားဖြင့်၊ အထက်ဖော်ပြပါ ကျွန်ုပ်တို့ဖြေရှင်းထားသော လေ့ကျင့်ခန်း၏ ဟာမိုနီဆိုလိုချက်ကို ရယူရန် Excel ဆဲလ် =MEDIA.ARMO(7;10;15;6;11) တွင် သင်ရေးပါ။

မည်သည့်တန်ဖိုးများသည် သုညဖြစ်ပါက၊ ကိန်းဂဏန်းတန်ဖိုးအစုတစ်ခု၏ ဟာမိုနီဆိုလိုအား သုညဟု မသတ်မှတ်နိုင်သောကြောင့် လုပ်ဆောင်ချက်သည် အမှားအယွင်းတစ်ခု ပြန်ဖြစ်သွားမည်ဖြစ်ကြောင်း မှတ်သားထားသင့်သည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။