ကိန်းဂဏန်းစာရင်းဇယားများတွင် ကျန်ရှိနေသော အရာများကား အဘယ်နည်း။

အကြွင်း သည် မှတ်သားထားသောတန်ဖိုးနှင့် ဆုတ်ယုတ်မှုခွဲခြမ်းစိတ်ဖြာမှုတွင် ခန့်မှန်းထားသော တန်ဖိုးကြား ကွာခြားချက်ဖြစ်သည်။

အောက်ပါအတိုင်း တွက်ချက်သည်။

လက်ကျန် = သတိပြုမိသော တန်ဖိုး – ခန့်မှန်းထားသော တန်ဖိုး

linear regression ၏ပန်းတိုင်သည် တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ကြိုတင်ခန့်မှန်းကိန်းရှင်များနှင့် တုံ့ပြန်မှုကိန်းရှင် ကြားရှိ ဆက်နွယ်မှုကို တွက်ချက်ရန်ဖြစ်ကြောင်း သတိရပါ။ ဒါကိုလုပ်ဖို့၊ linear regression သည် အနည်းဆုံး squares regression line ဟုခေါ်သော data နှင့် “ အံကိုက်” အသင့်တော်ဆုံးမျဉ်းကို ရှာဖွေသည်။

ဤမျဉ်းသည် ဒေတာအတွဲရှိ စောင့်ကြည့်မှု တစ်ခုစီအတွက် ခန့်မှန်းချက်တစ်ခုထုတ်ပေးသည်၊ သို့သော် ဆုတ်ယုတ်မှုမျဉ်းမှပြုလုပ်သော ခန့်မှန်းချက်သည် သတိပြုမိသောတန်ဖိုးနှင့် အတိအကျ ကိုက်ညီလိမ့်မည်မဟုတ်ပါ။

ခန့်မှန်းချက်နှင့် သတိပြုမိသော တန်ဖိုးကြား ခြားနားချက်မှာ အကြွင်းဖြစ်သည်။ ကျွန်ုပ်တို့ သတိပြုမိသော တန်ဖိုးများကို ရေးဆွဲပြီး တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုမျဉ်းကို ခြုံငုံမိပါက၊ ရှုမြင်မှုတစ်ခုစီအတွက် အကြွင်းအကျန်များသည် ရှုထောင့်နှင့် ဆုတ်ယုတ်မှုမျဉ်းကြား ဒေါင်လိုက်အကွာအဝေးဖြစ်လိမ့်မည်-

မှတ်သားမှုတစ်ခုတွင် ၎င်း၏တန်ဖိုးသည် ဆုတ်ယုတ်မှုမျဉ်းမှ ခန့်မှန်းထားသော တန်ဖိုးထက် ကြီးပါက အပြုသဘောဆောင်သော အကြွင်းအကျန်ရှိ သည်။

အပြန်အလှန်အားဖြင့်၊ ရှုမြင်မှုတစ်ခုတွင် ၎င်း၏တန်ဖိုးသည် ဆုတ်ယုတ်မှုမျဉ်းမှ ခန့်မှန်းထားသော တန်ဖိုးထက်နည်းပါက အနုတ်လက္ခဏာကျန်ရှိနေ ပါသည်။

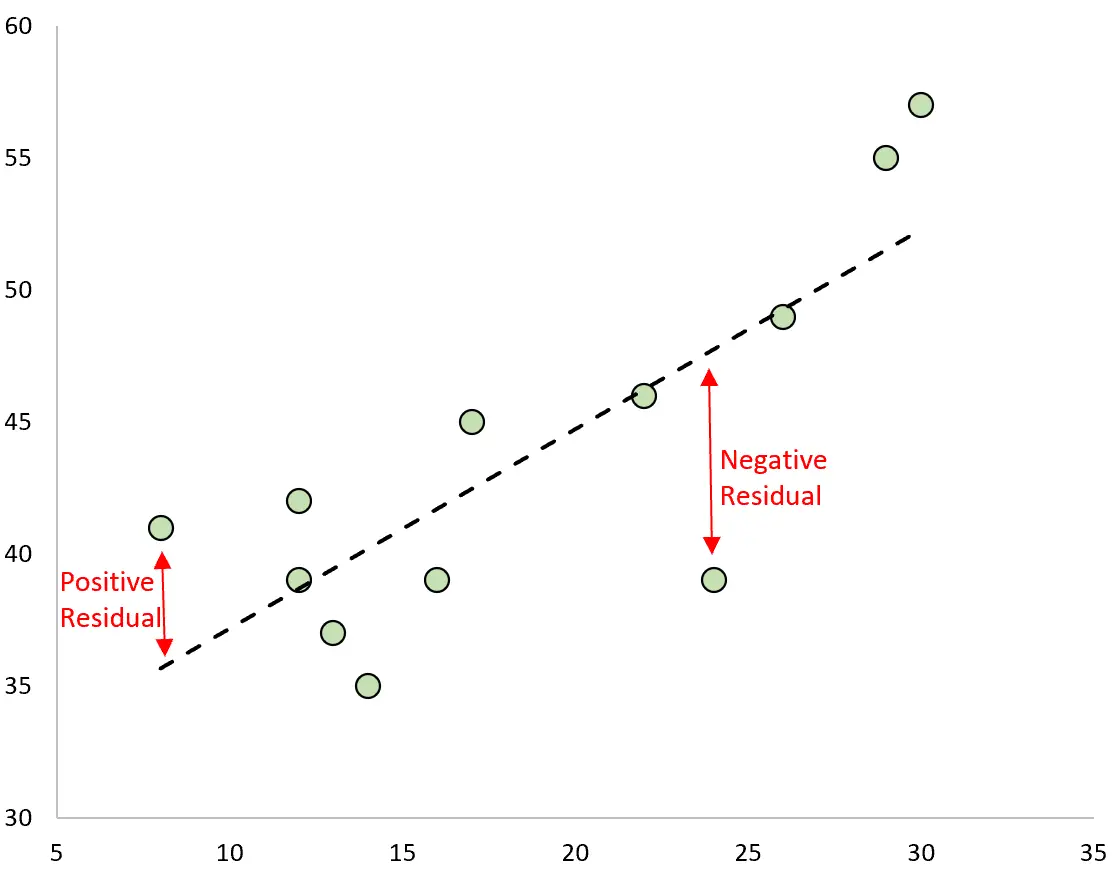
အချို့သော လေ့လာတွေ့ရှိချက်များသည် အပြုသဘောဆောင်သော အကြွင်းအကျန်များ ရှိမည်ဖြစ်ပြီး အခြားအရာများတွင် အနုတ်လက္ခဏာကျန်များ ရှိမည်ဖြစ်သော်လည်း ကျန်အကြွင်းအကျန်အားလုံးသည် သုညအထိ ပေါင်းသွားမည်ဖြစ်သည်။

အကြွင်းအကျန်များကို တွက်ချက်ခြင်း ဥပမာ

စုစုပေါင်း စောင့်ကြည့်မှု 12 ခုပါရှိသော အောက်ပါဒေတာအစုံရှိသည်ဆိုပါစို့။

ကျွန်ုပ်တို့သည် ဤဒေတာအတွဲအတွက် မျဉ်းကြောင်းကြောင်းဆုတ်ယုတ်မှုမျဉ်းအား ကိုက်ညီရန် ကိန်းဂဏန်းဆော့ဖ်ဝဲ ( R ၊ Excel ၊ Python ၊ Stata စသည်ဖြင့်) ကိုအသုံးပြုပါက၊ အသင့်တော်ဆုံးမျဉ်းသည်-

y = 29.63 + 0.7553x

ဤစာကြောင်းကိုအသုံးပြု၍ X ၏တန်ဖိုးအပေါ်အခြေခံ၍ Y တန်ဖိုးတစ်ခုစီအတွက် ခန့်မှန်းထားသောတန်ဖိုးကို တွက်ချက်နိုင်ပါသည်။ ဥပမာ၊ ပထမအကြိမ်လေ့လာခြင်း၏ ခန့်မှန်းတန်ဖိုးမှာ-

y = 29.63 + 0.7553*(8) = 35.67

ထို့နောက် ဤလေ့လာတွေ့ရှိချက်အတွက် ကျန်ရှိသော ပမာဏကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။

ကျန်ရှိသော = သတိပြုမိသောတန်ဖိုး – ခန့်မှန်းထားသောတန်ဖိုး = 41 – 35.67 = 5.33

လေ့လာမှုတစ်ခုစီအတွက် ကျန်နေသေးသည့်အရာများကို ရှာဖွေရန် ဤလုပ်ငန်းစဉ်ကို ထပ်လုပ်နိုင်ပါသည်။

တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုမျဉ်းဖြင့် ရှုမြင်သုံးသပ်ချက်များကို မြင်သာစေရန် scatterplot တစ်ခုကို ဖန်တီးပါက၊ အချို့သော လေ့လာတွေ့ရှိချက်များသည် မျဉ်းအထက်တွင် ရှိနေကြပြီး အချို့မှာ မျဉ်းအောက်၌ ရှိနေသည်ကို တွေ့ရပါမည်။

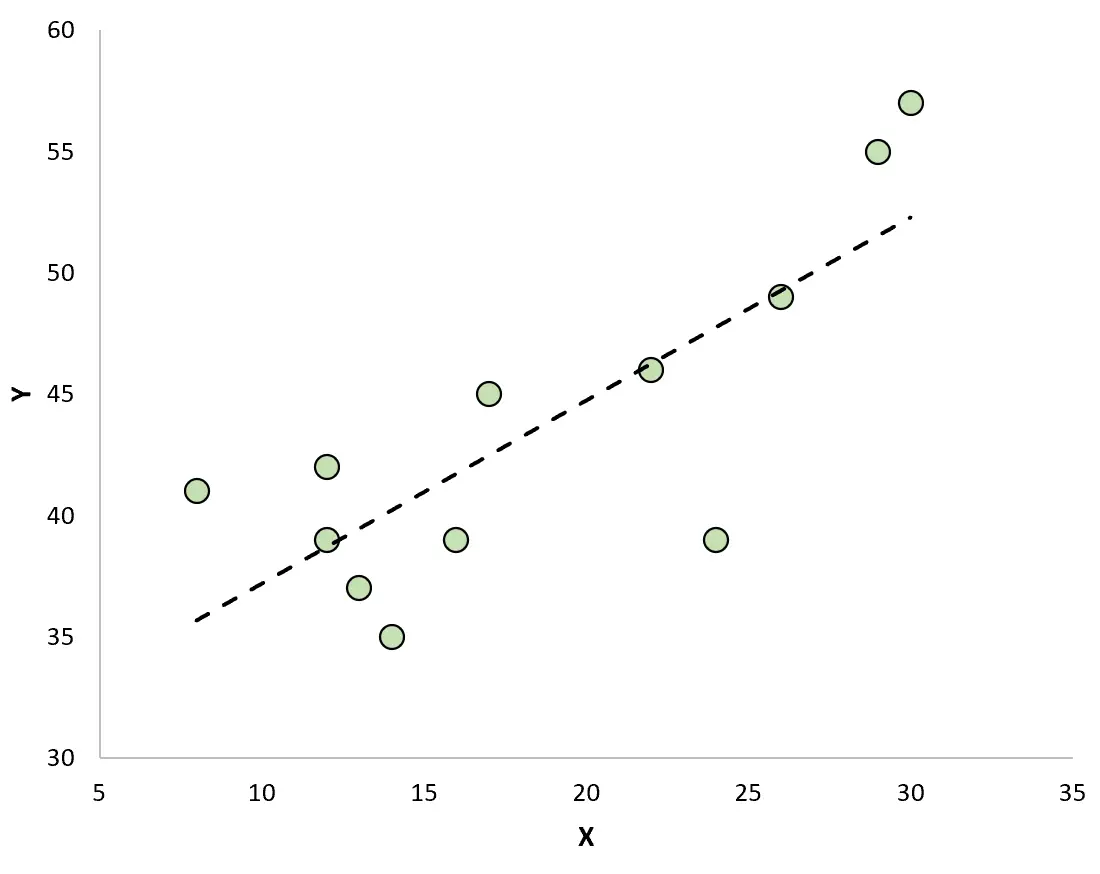
အကြွင်းအကျန်များ၏ဂုဏ်သတ္တိများ

အကြွင်းအကျန်များသည် အောက်ပါဂုဏ်သတ္တိများရှိသည်။

• ဒေတာအတွဲတစ်ခုရှိ စူးစမ်းမှုတစ်ခုစီတွင် သက်ဆိုင်သော အကြွင်းအကျန်တစ်ခုရှိသည်။ ထို့ကြောင့်၊ ဒေတာအတွဲတစ်ခုတွင် စုစုပေါင်း စူးစမ်းမှု 100 ပါ၀င်ပါက၊ မော်ဒယ်သည် ခန့်မှန်းတန်ဖိုး 100 ထုတ်ပေးမည်ဖြစ်ပြီး စုစုပေါင်း 100 ကျန်ရှိနေမည်ဖြစ်သည်။
• အကြွင်းအားလုံး၏ ပေါင်းလဒ်သည် သုညဖြစ်သည်။
• အကြွင်းအကျန်များ၏ ပျမ်းမျှတန်ဖိုးသည် သုညဖြစ်သည်။

အကြွင်းအကျန်များကို လက်တွေ့တွင် မည်သို့အသုံးပြုကြသနည်း။

လက်တွေ့တွင်၊ အကြွင်းအကျန်များကို ဆုတ်ယုတ်ခြင်းတွင် မတူညီသော အကြောင်းရင်းသုံးခုအတွက် အသုံးပြုသည်-

1. မော်ဒယ်၏ လုံလောက်မှုကို အကဲဖြတ်ပါ။

တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုမျဉ်းကို ကျွန်ုပ်တို့ထုတ်လုပ်ပြီးသည်နှင့်၊ ကျွန်ုပ်တို့သည် နှစ်ထပ်ကိန်းကျန်အကြွင်းအားလုံး၏ ပေါင်းလဒ်ဖြစ်သည့် လေးထပ်ပေါင်းလဒ် (RSS) ကို တွက်ချက်နိုင်သည်။ RSS နိမ့်လေ၊ ဆုတ်ယုတ်မှုပုံစံသည် ဒေတာနှင့် ကိုက်ညီလေလေဖြစ်သည်။

2. ပုံမှန်အနေအထားကို စစ်ဆေးပါ။

linear regression ၏ အဓိက ယူဆချက် တစ်ခုမှာ အကြွင်းအကျန်များကို ပုံမှန်အတိုင်း ဖြန့်ဝေနေခြင်း ဖြစ်သည်။

ဤယူဆချက်အား စမ်းသပ်ရန်အတွက်၊ ကျွန်ုပ်တို့သည် မော်ဒယ်၏ကျန်ရှိသော သာမာန်ဖြန့်ဝေမှုနောက်သို့ လိုက်ခြင်းရှိ၊ မရှိ ဆုံးဖြတ်ရန် ကျွန်ုပ်တို့အသုံးပြုနိုင်သည့် ကွက်အမျိုးအစားဖြစ်သည့် QQ ကွက်ကွက်ကို ဖန်တီးနိုင်သည်။

ကွက်ကွက်ပေါ်ရှိ အမှတ်များသည် အကြမ်းဖျင်းအားဖြင့် တည့်တည့် ထောင့်ဖြတ်မျဉ်းများ ဖြစ်ပေါ်လာပါက၊ ပုံမှန်ဖြစ်ခြင်း၏ ယူဆချက်နှင့် ကိုက်ညီပါသည်။

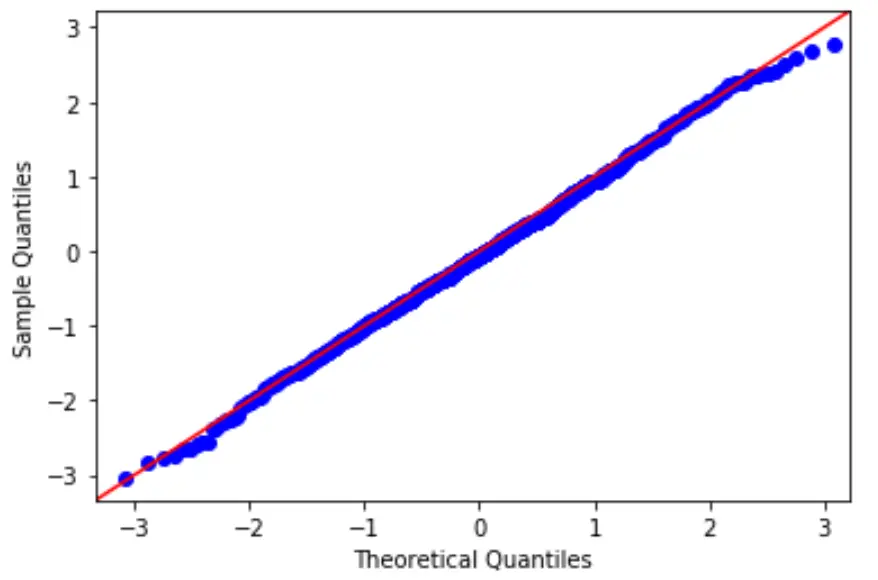
3. လိင်တူဆက်ဆံခြင်း၏ ယူဆချက်ကို စစ်ဆေးပါ။

linear regression ၏ နောက်ထပ်သော့ယူဆချက်မှာ အကြွင်းအကျန်များသည် x အဆင့်တစ်ခုစီတွင် အဆက်မပြတ်ကွဲလွဲနေခြင်းဖြစ်သည်။ ဒါကို Homoscedasticity လို့ခေါ်တယ်။ ဒီလိုမှမဟုတ်ရင် ကျန်တဲ့သူတွေဟာ မျိုးကွဲတွေ ကွဲကုန်တယ်။

ဤယူဆချက်နှင့်ကိုက်ညီခြင်းရှိ၊ မရှိ စစ်ဆေးရန်၊ မော်ဒယ်၏ ခန့်မှန်းတန်ဖိုးများနှင့် အကြွင်းအကျန်များကို ပြသသည့် အပိုင်းအစတစ်ခုဖြစ်သည့် အကြွင်းအကျန်များကို ဖန်တီးနိုင်သည်။

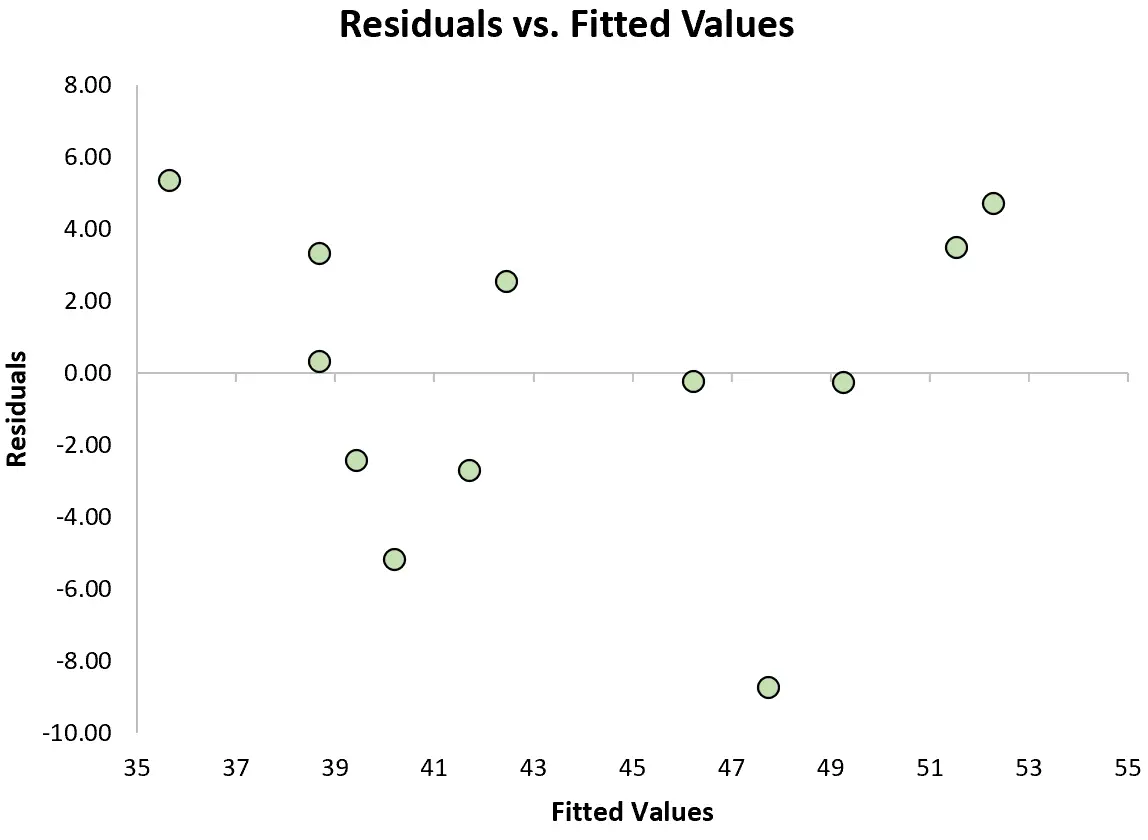
အကြွင်းအကျန်များကို ရှင်းရှင်းလင်းလင်းမရှိသော ဂရပ်ရှိ သုညဝန်းကျင်တွင် ခန့်မှန်းခြေ အညီအမျှ ဖြန့်ဝေပါက၊ ယေဘူယျအားဖြင့် ကျွန်ုပ်တို့သည် အမျိုးတူသားစပ်ခြင်း၏ ယူဆချက်နှင့် ကိုက်ညီသည်ဟု ဆိုသည်။

ထပ်လောင်းအရင်းအမြစ်များ

Simple Linear Regression နိဒါန်း
Multiple Linear Regression အကြောင်း နိဒါန်း
linear regression ၏ ယူဆချက်လေးခု
Excel တွင် Residual Plot ဖန်တီးနည်း