အချိုးကျ ဖြန့်ဖြူးခြင်း။

အားဖြင့် Benjamin Anderson ဩဂုတ် 5, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင်၊ အချိုးညီသောဖြန့်ဝေမှုများသည် အဘယ်အရာဖြစ်သည်၊ အချိုးညီသောဖြန့်ဝေမှုများ၏နမူနာများနှင့် ဖြန့်ဖြူးမှုတစ်ခုသည် အချိုးညီမှု သို့မဟုတ် အချိုးမညီခြင်းရှိ၊ မရှိ ဆုံးဖြတ်နည်းတို့ကို လေ့လာပါမည်။

အချိုးညီသော ဖြန့်ဝေမှုဆိုသည်မှာ အဘယ်နည်း။

ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ အချိုးညီသောဖြန့်ဝေမှုသည် ပျမ်းမျှ၏ဘယ်ဘက်တွင်ရှိသော ပျမ်းမျှတန်ဖိုးများနှင့်တူညီသောကိန်းဂဏန်းများရှိသည်။ တစ်နည်းဆိုရသော် အချိုးညီသော ဖြန့်ဝေမှုတွင် ပျမ်းမျှသည် အချိုးညီသော ဝင်ရိုးတစ်ခုဖြစ်သည်။

ဥပမာအားဖြင့်၊ ပုံမှန်ဖြန့်ဖြူးမှုသည် အချိုးကျသော ဖြန့်ဖြူးမှုဖြစ်သည်။

အချိုးညီသော ဖြန့်ဝေမှုအားလုံးတွင် ပျမ်းမျှသည် ပျမ်းမျှနှင့် ညီမျှသည်။ အကယ်၍ ဖြန့်ဝေမှုသည် ပုံမှန်မဟုတ်ပါက (စာရင်းအင်းမုဒ်သည် တန်ဖိုးတစ်ခုတည်း)၊ ပျမ်းမျှ၊ အလယ်အလတ်နှင့် မုဒ်သည် ညီမျှသည်။

ယုတ္တိနည်းအားဖြင့်၊ အချိုးကျ ဖြန့်ဝေမှုဆိုသည်မှာ အဘယ်အရာကို ဆိုလိုသည်၊ အလယ်အလတ်နှင့် မုဒ်တို့ကို ရှင်းရှင်းလင်းလင်း နားလည်ရန် လိုအပ်သည်။ ဤကိန်းဂဏန်းဆိုင်ရာ အယူအဆများ၏ အဓိပ္ပါယ်ကို ဤနေရာတွင် ပြန်လည်သုံးသပ်နိုင်ပါသည်။

➤ ကြည့်ပါ- ဆိုလိုချင်တာ၊ အလယ်အလတ်နဲ့ မုဒ်ဆိုတာ ဘာလဲ။

အချိုးညီသော ဖြန့်ဝေမှုများ၏ ဥပမာများ

အချိုးညီသော ဖြန့်ဖြူးမှု၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို ထည့်သွင်းစဉ်းစားခြင်းဖြင့်၊ ဤဖြန့်ဖြူးမှုအမျိုးအစား၏ ဥပမာကို အောက်တွင်ဖော်ပြထားသည်-

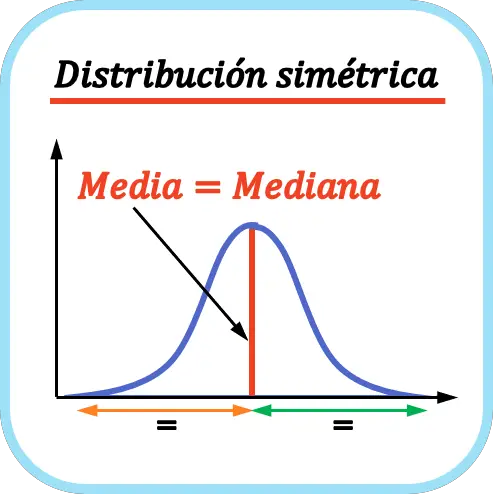
ဂရပ်တွင်ပြသထားသည့်အတိုင်း၊ ကိန်းဂဏန်းသည် အချက်အလက်အားလုံး၏အလယ်တွင် ညာဘက်တွင်တည်ရှိသောကြောင့်၊ မျဉ်းကွေး၏ဘယ်ဘက်ရှိ အမြီးသည် ညာဘက်ရှိအမြီးနှင့် တူညီသောကြောင့် ဖြန့်ဝေမှုသည် အချိုးညီညီဖြစ်သည်။ ဤကိစ္စတွင်၊ မုဒ်သည် စံနမူနာမရှိသောကြောင့် ပျမ်းမျှ၊ အလယ်အလတ်နှင့် မုဒ်တို့သည် တူညီသည်။

အချိုးကျဖြစ်နိုင်ခြေဖြန့်ဝေမှု အမျိုးအစားနှစ်ခု၏ ရှင်းရှင်းလင်းလင်း ဥပမာနှစ်ခုမှာ ပုံမှန်ဖြန့်ဖြူးမှုနှင့် တူညီသောဖြန့်ဝေမှုဖြစ်ပြီး ၎င်းတို့တွင် ဆိုလိုရင်း၏ ဘယ်နှင့်ညာဘက်တွင် တန်ဖိုးများ တူညီသောကြောင့်ဖြစ်သည်။

အခြားတစ်ဖက်တွင်၊ ဖြန့်ဖြူးမှုတစ်ခုသည် အချိုးကျနှင့် bimodal ဖြစ်သည်၊ ဆိုလိုသည်မှာ မုဒ်နှစ်ခုရှိသည်။ အောက်ပါဥပမာကိုကြည့်ပါ-

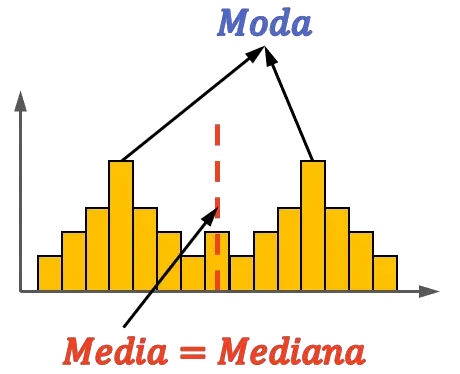
ဤအခြားဥပမာတွင် သင်တွေ့မြင်ရသည့်အတိုင်း၊ bimodal distribution သည် အခြားတန်ဖိုးများမခွဲခြားဘဲ အလယ်ဗဟိုတွင် ပျမ်းမျှနှင့် အလယ်အလတ်ရှိနိုင်သောကြောင့်၊ သို့သော်လည်း ဤကိစ္စတွင်၊ မုဒ်သည် ပျမ်းမျှနှင့် မုဒ်နှင့် တူညီနေရန် မလိုအပ်ပါ။

၎င်းတို့၏ symmetry အရ အခြားသော ဖြန့်ဖြူးမှုအမျိုးအစားများ

အချိုးညီသော ဖြန့်ဝေမှုများအပြင်၊ အချိုးမညီသော ဖြန့်ဝေမှု အမျိုးအစား နှစ်မျိုးရှိသည်။

Symmetric distribution : ဖြန့်ဖြူးမှုတွင် ပျမ်းမျှ၏ ဘယ်နှင့်ညာတွင် တူညီသောတန်ဖိုးများရှိသည်။
အပြုသဘောဆောင်သော လှည့်ဖြားထားသော ဖြန့်ဝေမှု – ဖြန့်ဖြူးမှုသည် ၎င်း၏ဘယ်ဘက်ထက် ပျမ်းမျှ၏ညာဘက်တွင် တန်ဖိုးများပိုမိုကွဲပြားသည်။
အပျက်သဘောဆောင်သော လှည့်ဖြားထားသော ဖြန့်ဝေမှု – ဖြန့်ဖြူးမှုသည် ၎င်း၏ညာဘက်ထက် ပျမ်းမျှ၏ဘယ်ဘက်တွင် ပိုမိုကွဲပြားသောတန်ဖိုးများရှိသည်။

ဖြန့်ဖြူးမှုတစ်ခုသည် အချိုးညီမှုရှိမရှိကို မည်သို့ပြောနိုင်မည်နည်း။

ဖြန့်ဖြူးမှုတစ်ခုသည် အချိုးညီမှုရှိမရှိ ဆုံးဖြတ်ရန်၊ ဖော်မြူလာဖြစ်သည့် Pearson asymmetry coefficient ကို တွက်ချက်ရပါမည်။

$A_p=\cfrac{\mu-Mo}{\sigma}$

ရွှေ

$A_p$

Pearson coefficient ဖြစ်သည်၊

$\mu$

ဂဏန်းသင်္ချာဆိုလို၊

$Mo$

မုဒ် (စာရင်းအင်း) နှင့်

$\sigma$

စံသွေဖည်။

ထို့ကြောင့်၊ Pearson asymmetry coefficient ၏ နိမိတ်ပေါ် မူတည်၍ ဖြန့်ဖြူးမှုသည် အချိုးညီသော သို့မဟုတ် အချိုးမညီသော ဖြစ်လိမ့်မည်-

Pearson skewness coefficient သည် အပြုသဘောဆောင်ပါက၊ ဖြန့်ဖြူးမှုသည် အပြုသဘောဖြင့် လွဲနေသည်ဟု ဆိုလိုသည်။
Pearson skewness coefficient သည် အနှုတ်ဖြစ်ပါက၊ ၎င်းသည် ဖြန့်ဖြူးမှုသည် အနုတ်လက္ခဏာဘက်သို့ လှည့်သွားသည်ဟု ဆိုလိုသည်။
Pearson coefficient of skewness သည် သုညဖြစ်ပါက၊ ဖြန့်ဖြူးမှုသည် အချိုးကျသည်ဟု ဆိုလိုသည်။

သို့သော်လည်း၊ Pearson coefficient ကို ဖြန့်ဝေမှုသည် ပုံမှန်မဟုတ်လျှင်သာ တွက်ချက်နိုင်သည်၊ သို့မဟုတ်ပါက အောက်ပါအတိုင်း ပုံသေနည်းဖြစ်သည့် Fisher asymmetry coefficient ကို အသုံးပြုရန် လိုအပ်သည်-

$\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\mu\right)^3}{N\cdot \sigma ^3}$

ရွှေ

$\mu$

ဂဏန်းသင်္ချာဆိုလို၊

$\sigma$

စံသွေဖည်မှုနှင့်

$N$

စုစုပေါင်းဒေတာ။

Fisher asymmetry coefficient ၏ အဓိပ္ပာယ်ဖွင့်ဆိုချက်သည် Pearson coefficient နှင့် ထပ်တူဖြစ်သည်- ၎င်းသည် အပြုသဘောဆောင်ပါက၊ ဖြန့်ဖြူးမှုသည် အပြုသဘောမညီဟု ဆိုလိုသည်၊ ၎င်းသည် အနုတ်လက္ခဏာဖြစ်လျှင် ဖြန့်ဝေမှုသည် အနှုတ်လက္ခဏာမညီဘဲ၊ သုညဖြစ်လျှင် ဖြန့်ဝေမှုသည် အချိုးကျသည်ဟု ဆိုလိုသည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။