အချိုးကျနမူနာ
ဤဆောင်းပါးတွင် ကျွန်ုပ်တို့သည် အစီအစဥ်နမူနာကို မည်ကဲ့သို့လုပ်ဆောင်ကြောင်း ရှင်းပြထားသည်။ ဤနေရာတွင် အလွှာလိုက်နမူနာ၏ အမျိုးအစားခွဲများ၏ ရှင်းလင်းချက်နှင့် နောက်ဆုံးတွင် အစီအစဥ်နမူနာ၏ အားသာချက်များနှင့် အားနည်းချက်များကား အဘယ်နည်း။
အစီအစဥ်နမူနာဆိုသည်မှာ အဘယ်နည်း။
Stratified sampling သည် လူဦးရေကို အုပ်စုများအဖြစ် ပိုင်းခြားပြီး (စထရာတာဟုခေါ်သည်) ဖြင့် နမူနာ၏ဒြပ်စင်များကို ရွေးချယ်ရန် အသုံးပြုသည့် ကိန်းဂဏန်းဆိုင်ရာ နည်းလမ်းတစ်ခုဖြစ်သည်။ ဆိုလိုသည်မှာ အစီအစဥ်နမူနာတွင်၊ လူဦးရေကို strata များအဖြစ် ပိုင်းခြားထားပြီး stratum တစ်ခုစီမှ တစ်ဦးချင်းစီကို လေ့လာမှုနမူနာတစ်ခုလုံးအတွက် ကျပန်းရွေးချယ်ထားသည်။
Strata သည် တစ်သားတည်းဖြစ်နေသော အုပ်စုများ သို့မဟုတ် တစ်နည်းအားဖြင့် stratum အတွင်းရှိ လူတစ်ဦးချင်းစီတွင် ၎င်းတို့ကို အခြားသော strata နှင့် ကွဲပြားစေသော ကိုယ်ပိုင်လက္ခဏာများရှိသည်။ ထို့ကြောင့် လူတစ်ဦးသည် အလွှာတစ်ခုတည်းတွင်သာ သက်ဆိုင်ပါသည်။
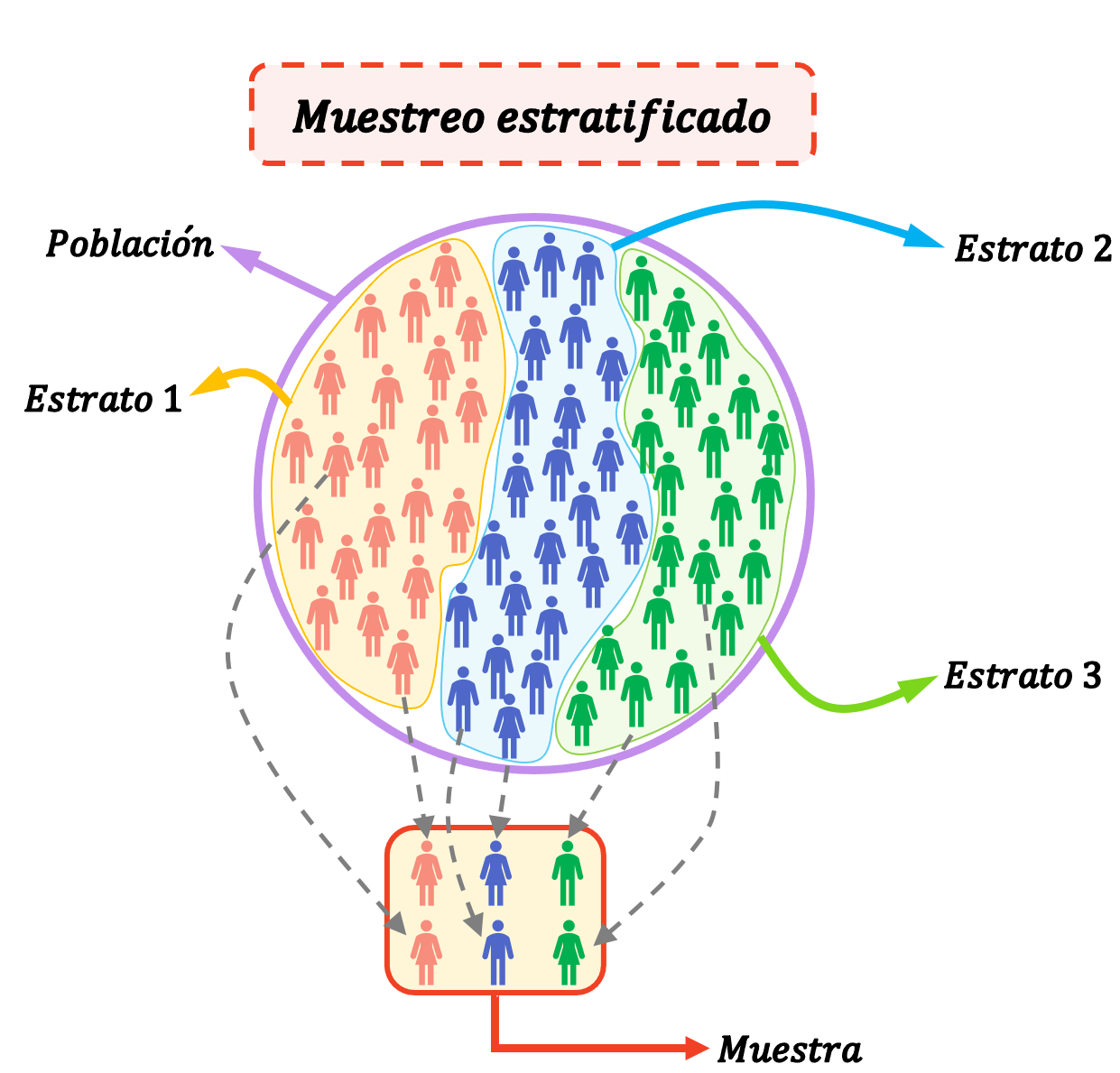
လူဦးရေကို တစ်သားတည်းဖြစ်စေသော အုပ်စုများဖြင့် ဖွဲ့စည်းထားသောအခါတွင် အချိုးကျနမူနာသည် အလွန်အသုံးဝင်ပါသည်။
ယုတ္တိနည်းအားဖြင့်၊ အလွှာအားလုံး၏ အရွယ်အစား ပေါင်းလဒ်သည် စာရင်းအင်းလူဦးရေ၏ အရွယ်အစားကို ပေးသည်-
![]()
အလားတူ၊ စထရာတမ်တစ်ခုစီတွင် ရွေးချယ်ထားသော နမူနာအရွယ်အစား၏ ပေါင်းလဒ်သည် စာရင်းအင်းလေ့လာမှု၏ စုစုပေါင်းနမူနာအရွယ်အစားနှင့် ညီမျှသည်-
![]()
လူဦးရေ သို့မဟုတ် နမူနာကို အသီးသီး သတ်မှတ်ရန် ကျွန်ုပ်တို့သည် ယေဘုယျအားဖြင့် စာလုံးကြီးနှင့် စာလုံးငယ်များအကြား ကွဲပြားပါသည်။
အချိုးကျနမူနာပြုလုပ်နည်း
အချိုးကျနမူနာလုပ်ဆောင်ရန် အဆင့်များမှာ အောက်ပါအတိုင်းဖြစ်သည်။
- ပစ်မှတ်လူဦးရေကို သတ်မှတ်ပါ။
- ကွဲပြားနိုင်သော stratification ကို ရွေးချယ်ပြီး strata မည်မျှရှိမည်နည်း။
- လူဦးရေ၏ အစိတ်အပိုင်းတစ်ခုစီတွင် မည်သည့် stratum ကို ခွဲခြားသတ်မှတ်ပါ။
- နမူနာ၏ အစိတ်အပိုင်းဖြစ်မည့် stratum တစ်ခုစီ၏ အရွယ်အစားကို တွက်ချက်ပါ။
- လေ့လာမှုနမူနာနှင့် သက်ဆိုင်မည့် အလွှာတစ်ခုစီမှ အစိတ်အပိုင်းများကို ကျပန်းရွေးချယ်ပါ ။ အဆင့်တစ်ခုစီအတွက်၊ ယခင်အဆင့်တွင် ဆုံးဖြတ်ထားသည့်အတိုင်း အစိတ်အပိုင်းများစွာကို ရွေးချယ်ရမည်ဖြစ်သည်။
နမူနာတွင် stratum တစ်ခုစီ၏အရွယ်အစားသည် stratum ၏အရွယ်အစားပေါ်တွင်သာမက stratum sampling အမျိုးအစားပေါ်တွင်လည်းမူတည်ကြောင်း မှတ်သားထားပါ။ ထို့နောက်၊ နမူနာပုံစံတစ်ခုစီကို အမျိုးအစားတစ်ခုစီနှင့် stratum တစ်ခုစီ၏နမူနာအရွယ်အစားကို နမူနာတစ်ခုအသုံးပြု၍ တွက်ချက်ပုံကို ရှင်းပြထားသည်။
Stratified Sampling အမျိုးအစားများ
ယခုအခါတွင် အစီအစဥ်နမူနာ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို သင်သိပြီးဖြစ်၍ အောက်ပါအတိုင်း အမျိုးအစားခွဲခြားထားသည့် အစီအစဥ်နမူနာအမျိုးအစားများစွာရှိကြောင်း သိထားသင့်သည်-
- အချိုးကျ အချိုးကျနမူနာ
- Uniform Stratified Sampling
- နမူနာယူခြင်းသည် အကောင်းဆုံးဖြစ်သည် ။
တစ်ခုချင်းစီ၏ အဓိပ္ပါယ်ကို ပိုမိုနားလည်ရန် အမျိုးအစားတစ်ခုစီကို အောက်တွင် အသေးစိတ်ရှင်းပြထားသည်။
အချိုးကျ အချိုးကျနမူနာ
အချိုးကျနမူနာ သို့မဟုတ် အချိုးကျခွဲဝေမှုနမူနာတွင်၊ လေ့လာမှုနမူနာ၏တစ်စိတ်တစ်ပိုင်းဖြစ်သော စတန်းတမ်တစ်ခုစီမှဒြပ်စင်အရေအတွက်သည် စထရမ်တစ်ခုစီ၏အရွယ်အစားနှင့် အချိုးကျပါသည်။
ထို့ကြောင့် စထရမ်တစ်ခုသည် အခြားတစ်ခုထက် ပိုကြီးပါက၊ နောက်ဆုံးနမူနာတွင် အဆိုပါ stratum မှ ဒြပ်စင်များ ပိုမိုပါဝင်မည်ဖြစ်သည်။ အခြားတစ်ဖက်တွင်၊ stratum တစ်ခုသည် အခြားတစ်ခုထက်ငယ်ပါက၊ ကိန်းဂဏန်းခွဲခြမ်းစိတ်ဖြာမှုနမူနာတွင် ဤ stratum မှဒြပ်စင်များ အနည်းငယ်သာရှိလိမ့်မည်။
strata သည် မတူညီသောအရွယ်အစားများဖြစ်ပြီး နမူနာကို ပိုကြီးသော strata မှဒြပ်စင်များပိုမိုပါဝင်စေလိုသောအခါတွင် ဤအမျိုးအစား stratified နမူနာပုံစံသည် အသုံးဝင်ပါသည်။
နမူနာတွင်ရှိမည့် stratum တစ်ခုစီမှ ဒြပ်စင်အရေအတွက်ကို တွက်ချက် ရန်၊ stratum တစ်ခုစီ၏ အရွယ်အစားကို strata အားလုံး၏ အရွယ်အစားပေါင်းလဒ်ဖြင့် ပိုင်းခြားရပါမည်။ ရလဒ်သည် နမူနာတွင် ထည့်သွင်းသင့်သည့် stratum အချိုးအစားဖြစ်လိမ့်မည်၊ ထို့ကြောင့် ၎င်းကို လိုချင်သောနမူနာအရွယ်အစားဖြင့် မြှောက်ရန် လိုအပ်မည်ဖြစ်သည်။
![]()
ရွှေ
![]()
လိုချင်သော စုစုပေါင်း နမူနာအရွယ်အစား၊
![]()
stratum ရှိ element အရေအတွက်
![]()
နမူနာတွင် ထည့်သွင်းရမည့်၊
![]()
stratum အရွယ်အစား
![]()
, နှင့်
![]()
လူဦးရေ စုစုပေါင်း အစိတ်အပိုင်းများ။
ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် အလုပ်သမား ၁၅၀ ရှိသော ကုမ္ပဏီတစ်ခုတွင် လေ့လာမှုတစ်ခုပြုလုပ်ပြီး လူ ၅၀ ကိုနမူနာယူကာ အလုပ်သမားများ၏အသက်အရွယ်ပေါ်မူတည်၍ အချက်အလက်များကို ခွဲခြမ်းစိတ်ဖြာကြည့်ချင်သည်။ ဒေတာများကို အောက်ပါအတိုင်း ကျွန်ုပ်တို့ ခွဲခြားနိုင်ပါသည်။
- အသက် 20 မှ 29 နှစ်ကြား အလုပ်သမား 35 ဦး
- အသက် 30 မှ 39 နှစ်အထိ – ဝန်ထမ်း 57 ဦး
- အသက် ၄၀ မှ ၄၉ နှစ်ကြား ဝန်ထမ်း ၄၂ ဦး
- အသက် 50 မှ 59 နှစ်အထိ – ဝန်ထမ်း 16 ဦး
ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် ဒေတာကို အချိုးကျ ခွဲထားမည်ဆိုလျှင်၊ နမူနာသည် အောက်ပါအတိုင်း ဖြစ်လိမ့်မည်။
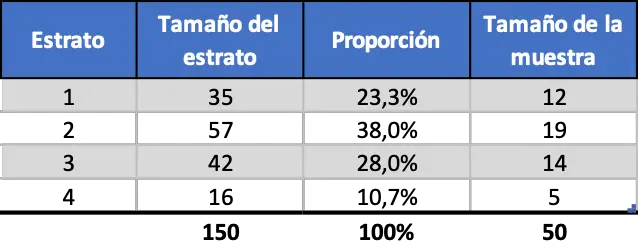
Uniform Stratified Sampling
ယူနီဖောင်းအစီအစဥ်နမူနာ သို့မဟုတ် ယူနီဖောင်းဆက်နွယ်မှုနမူနာတွင်၊ လေ့လာမှုနမူနာ၏အစိတ်အပိုင်းတစ်ခုစီမှ အစိတ်အပိုင်းအရေအတွက်သည် ညီမျှသည်။
ထို့ကြောင့် stratum တစ်ခုစီသည် ဤနမူနာပုံစံတွင် တူညီသောအလေးချိန်ရှိသည်။ stratum တစ်ခုတွင် အခြားသော stratum ထက်ပိုသော လူများ သို့မဟုတ် နည်းပါးသည်ဖြစ်စေ အားလုံးကို တူညီသော လူအရေအတွက်ဖြင့် နမူနာတွင် ကိုယ်စားပြုမည်ဖြစ်သည်။
ဤအခြေအနေတွင်၊ စထရာတမ်တစ်ခုစီရှိ ဒြပ်စင်များ၏အရွယ်အစားကို တွက်ချက်ရန်၊ လိုချင်သောနမူနာအရွယ်အစားကို ရှိပြီးသား strata အရေအတွက်ဖြင့် ပိုင်းခြားရပါမည်။ တစ်နည်းအားဖြင့်၊ အောက်ပါပုံသေနည်းကို အသုံးပြုသင့်သည်-
![]()
ရွှေ
![]()
လိုချင်သော စုစုပေါင်း နမူနာအရွယ်အစား၊
![]()
stratum ရှိ element အရေအတွက်
![]()
နမူနာတွင် ပါဝင်မည့်သူများနှင့်
![]()
လူဦးရေ ပိုင်းခြားထားသော အမျိုးအစား အရေအတွက်။
ယခင်နမူနာအတိုင်း၊ ကျွန်ုပ်တို့သည် အလုပ်သမား 50 ၏နမူနာကို လိုချင်ပြီး စုစုပေါင်း အမျိုးအစား 4 မျိုးရှိသောကြောင့်၊ stratum တစ်ခုစီ၏နမူနာအရွယ်အစားသည်-
![]()
ရလဒ်မှာ ဒဿမဂဏန်းဖြစ်ပြီး၊ အချို့သောအဆင့်တွင် အလုပ်သမား ၁၂ ဦးနှင့် အခြားလုပ်သား ၅၀ ဦးအထိ ၁၃ ဦးရှိမည်ဖြစ်သည်။ ထို့ကြောင့် တူညီသော အစီအစဥ်နမူနာသည် အောက်ပါအတိုင်းဖြစ်သည်။
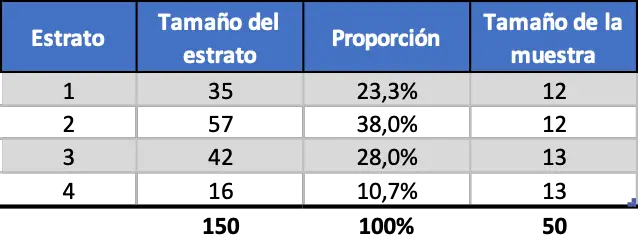
သင်တွေ့မြင်ရသည့်အတိုင်း၊ stratum တစ်ခုစီ၏နမူနာအရွယ်အစားသည် တစ်ခုချင်းစီ၏အချိုးအစားနှင့် သီးခြားဖြစ်သည်။
အကောင်းဆုံး အမျိုးအစားခွဲနမူနာ
အကောင်းမွန်ဆုံး အစီအစဥ်နမူနာ တွင်၊ stratum တစ်ခုစီရှိ ဒြပ်စင်အရေအတွက်သည် stratum တစ်ခုစီ၏ ကွဲပြားမှုအပေါ် အချိုးကျစွာ မူတည်ပါသည်။
ထို့ကြောင့်၊ ပိုကြီးသောပြောင်းလဲနိုင်မှုရှိသော strata သည် ပိုကြီးသောနမူနာအရွယ်အစားရှိမည်ဖြစ်ပြီး အပြန်အလှန်အားဖြင့် ကွဲပြားမှုနည်းသော strata သည် သေးငယ်သောနမူနာအရွယ်အစားရှိမည်ဖြစ်သည်။
စာရင်းအင်းလေ့လာမှုနမူနာ၏ တစ်စိတ်တစ်ပိုင်းဖြစ်သည့် စတန်းတမ်တစ်ခုစီမှ ဒြပ်စင်မည်မျှရှိသည်ကို ဆုံးဖြတ်ရန် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်-
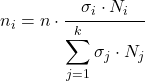
ရွှေ
![]()
စုစုပေါင်းနမူနာအရွယ်အစားသည် အလိုရှိသော၊
![]()
stratum အတွင်းရှိ element အရေအတွက်
![]()
နမူနာတွင် ထည့်သွင်းရမည့်၊
![]()
stratum ၏ စံသွေဖည်မှု (သို့မဟုတ် ပုံမှန်သွေဖည်မှု) ဖြစ်သည်။
![]()
, နှင့်
![]()
stratum ၏အရွယ်အစားဖြစ်သည်။
![]()
.
Stratified Sampling ၏ အားသာချက်များနှင့် အားနည်းချက်များ
Stratified Sampling တွင် အောက်ပါ အားသာချက်များနှင့် အားနည်းချက်များ ရှိပါသည်။
| အားသာချက် | အားနည်းချက်များ |
|---|---|
| ၎င်းသည် လူဦးရေတစ်ခုလုံးကိုသာမက သီးခြား stratum တစ်ခုစီကိုပါ ကိန်းဂဏန်းအရ လေ့လာနိုင်စေသည်။ | ၎င်းသည် အကောင်အထည်ဖော်ရန် ရှုပ်ထွေးသော နမူနာပုံစံတစ်ခုဖြစ်သည်။ |
| အချိုးကျနမူနာဖြင့် ကျူးလွန်သောနမူနာအမှားသည် ရိုးရှင်းသောကျပန်းနမူနာ၏ထက် အမြဲတန်းတူ သို့မဟုတ် နည်းပါးသည်။ | ဤသည်မှာ အချိန်ကုန်ပြီး စျေးကြီးသော နမူနာယူသည့် လုပ်ငန်းစဉ်ဖြစ်သည်။ |
| ၎င်းသည် လူဦးရေဆိုင်ရာ သုတေသီ၏ အသိပညာကို အခွင့်ကောင်းယူနိုင်စေပါသည်။ | ခွဲခြမ်းစိပ်ဖြာထားသော နမူနာတွင် အချက်အလက်များစွာ လိုအပ်ပါသည်။ |
| အစီအစဥ်နမူနာဖြင့်၊ stratum တစ်ခုစီမှ အနည်းဆုံး ဒြပ်စင်တစ်ခုကို နမူနာတွင် ထည့်သွင်းထားကြောင်း သေချာပါသည်။ | နမူနာကောက်ယူခြင်းကို ဆောင်ရွက်နိုင်ရန် အမျိုးအစားတစ်ခုစီ၏ အချိုးအစားကို သိရှိရန် လိုအပ်ပါသည်။ |
အစီအစဥ်နမူနာ၏ အဓိကလက္ခဏာမှာ လူဦးရေကို ပိုင်းခြားထားသော အုပ်စုတစ်ခုစီ သို့မဟုတ် စထရမ်တစ်ခုစီကို စာရင်းအင်းပိုင်းခြားစိတ်ဖြာရန် အသုံးပြုသည်။ ဟုတ်ပါတယ်၊ လူဦးရေတစ်ခုလုံးကိုလည်း ဒီနမူနာပုံစံနဲ့လည်း လေ့လာနိုင်ပါတယ်။ ထို့အပြင် strata သည် တစ်ခုနှင့်တစ်ခု မတူညီပါက data stratification ၏ အကျိုးကျေးဇူးများ ပိုမိုများပြားမည်ဖြစ်ပါသည်။
ဆန့်ကျင်ဘက်အနေနှင့်၊ နမူနာကောက်ယူခြင်းကို ဆောင်ရွက်နိုင်စေရန် ဒေတာကို အချိုးကျသတ်မှတ်ခြင်းသည် နမူနာကောက်ယူခြင်း၏ ရှုပ်ထွေးမှုတိုးလာပြီး အခြားသောနမူနာပုံစံများနှင့် နှိုင်းယှဉ်ပါက လုပ်ဆောင်ရန် ပိုမိုရှုပ်ထွေးလာခြင်းကို ဆိုလိုပါသည်။ stratification မှန်ကန်စွာပြုလုပ်ရန် အချိန်ယူရသောကြောင့် ဤပိုင်ဆိုင်မှုသည် စျေးကြီးသောနမူနာတစ်ခုဖြစ်ကြောင်းလည်း ရည်ညွှန်းပါသည်။
အစီအစဥ်နမူနာ၏နောက်ထပ်အားနည်းချက်မှာ ရိုးရှင်းသောကျပန်းနမူနာကဲ့သို့ အခြားနမူနာပုံစံများတွင် မလိုအပ်သည့် လေ့လာလိုသော လူဦးရေနှင့်ပတ်သက်သော အချက်အလက်များစွာ လိုအပ်ပါသည်။ သုတေသီသည် နယ်ပယ်တွင် ကြီးမားသောအသိပညာရှိလျှင် ဤအားနည်းချက်ကို လျော့ပါးစေနိုင်သည်။
နောက်ဆုံးတွင်၊ အစီအစဥ်နမူနာဖြင့်၊ အခြားနမူနာအမျိုးအစားများထက် လူဦးရေ၏ကိုယ်စားပြုမှုပိုရှိသောနမူနာကို ကျွန်ုပ်တို့ရရှိသည်၊ အကြောင်းမှာ စတန်းတမ်တစ်ခုစီမှဒြပ်စင်များပါဝင်ကြောင်းသေချာသောကြောင့်ဖြစ်သည်။ ဆန့်ကျင်ဘက်အားဖြင့်၊ အခြားနမူနာများတွင် ထွက်ပေါ်လာသောနမူနာတွင် မည်သည့် stratum မှ မည်သည့်ဒြပ်စင်မှ မပါဝင်နိုင်ပါ။