Symmetrical histogram ဆိုတာ ဘာလဲ။ (အဓိပ္ပါယ်နှင့် ဥပမာများ)

ဟီစတိုဂရမ် ဆိုသည်မှာ ဒေတာအတွဲတစ်ခုတွင် တန်ဖိုးများ၏ ကြိမ်နှုန်းကို မြင်ယောင်နိုင်ရန် ကူညီပေးသော ဇယားအမျိုးအစားတစ်ခုဖြစ်သည်။

စီမက်ထရီဟစ်စတိုဂရမ် သည် ၎င်း၏အလယ်ဗဟိုတွင် မျဉ်းတစ်ကြောင်းဆွဲလျှင် လုံးဝတူညီသောတစ်ဝက်များပါရှိသော ဟစ်စတိုဂရမ်အမျိုးအစားတစ်ခုဖြစ်သည်။

တူညီသော စီမက်ထရစ် ဟီစတိုဂရမ် အမျိုးအစား နှစ်မျိုးရှိသည်။

• Unimodal symmetric histogram − အထွတ်အထိပ်ရှိသော ဟစ်စတိုဂရမ်
• Symmetric bimodal histogram − အထွတ်အထိပ်နှစ်ခုပါသည့် ဟစ်စတိုဂရမ်

အောက်ပါဥပမာများသည် ဤ histogram တစ်ခုစီ၏ပုံသဏ္ဍာန်ကိုပြသသည်။

ဥပမာ 1- Unimodal symmetric histogram

အောက်ပါ ဟစ်စတိုဂရမ်သည် unimodal symmetric histogram ၏ ဥပမာတစ်ခုဖြစ်သည်။

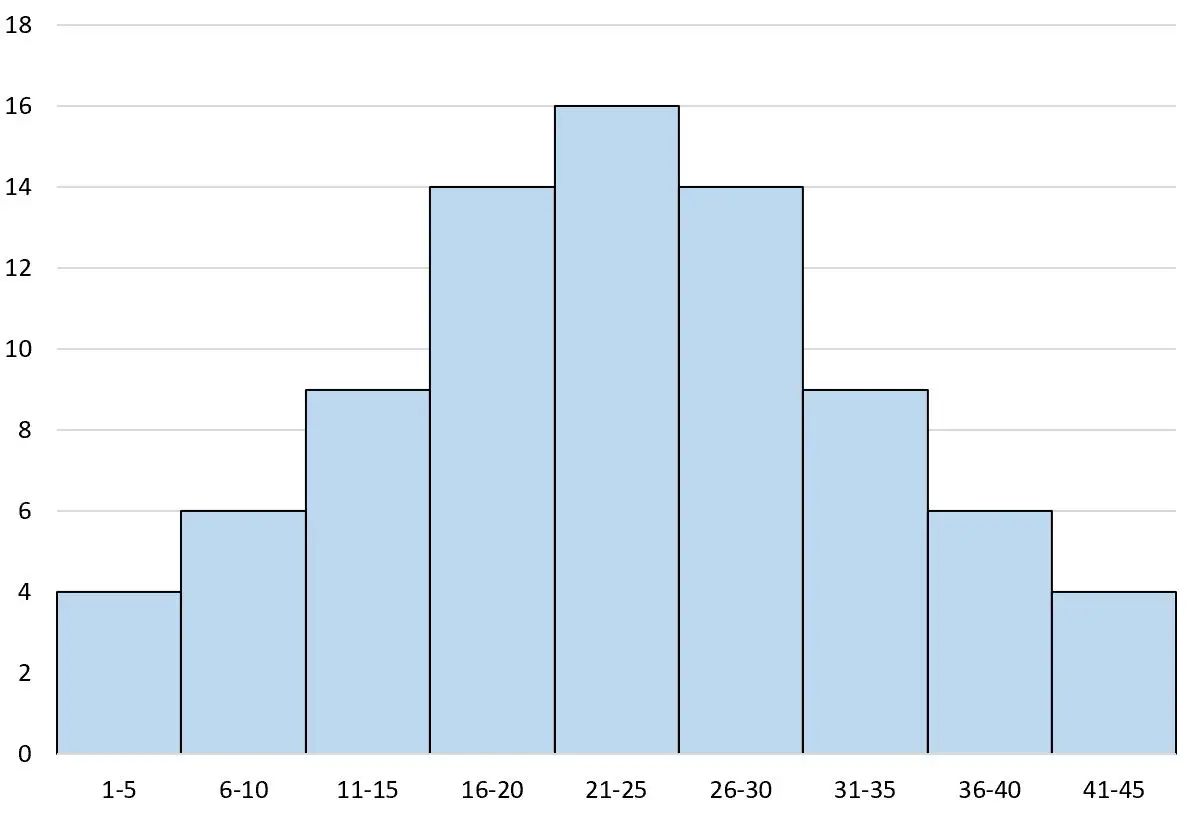
ဟီစတိုဂရမ်၏ အလယ်ဗဟိုတွင် မျဉ်းတစ်ကြောင်းဆွဲမည်ဆိုလျှင်၊ ဘယ်နှင့်ညာ နှစ်ဖက်သည် အတိအကျတူညီလိမ့်မည်-

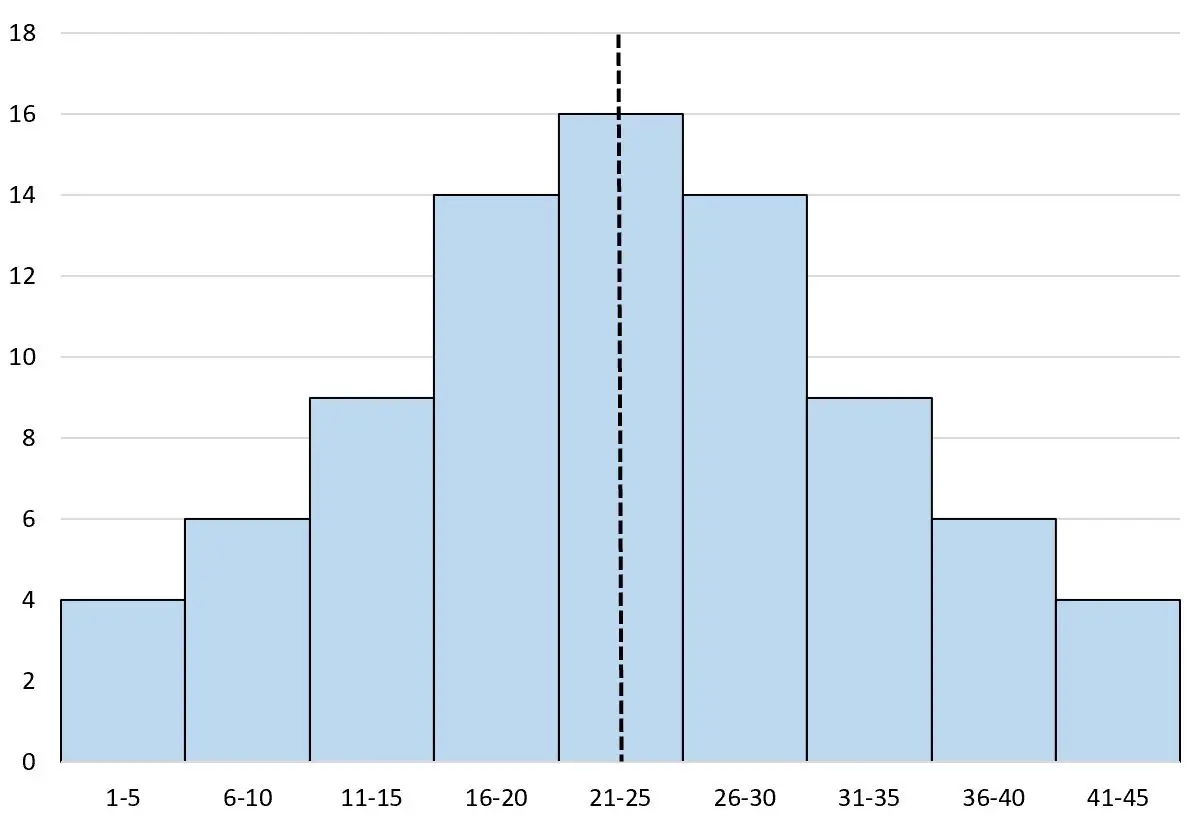
“ plain” ဆိုသည်မှာ “ တစ်ခု” ဖြစ်ပြီး ဤ histogram သည် အလယ်တွင် တိုက်ရိုက် အထွတ်အထိပ်တစ်ခုသာ ရှိသောကြောင့် ၎င်းကို unimodal symmetric histogram ဟုခေါ်ပါသည်။

ဥပမာ 2- Symmetric bimodal histogram

အောက်ပါ histogram သည် bimodal symmetric histogram ၏ ဥပမာတစ်ခုဖြစ်သည်။

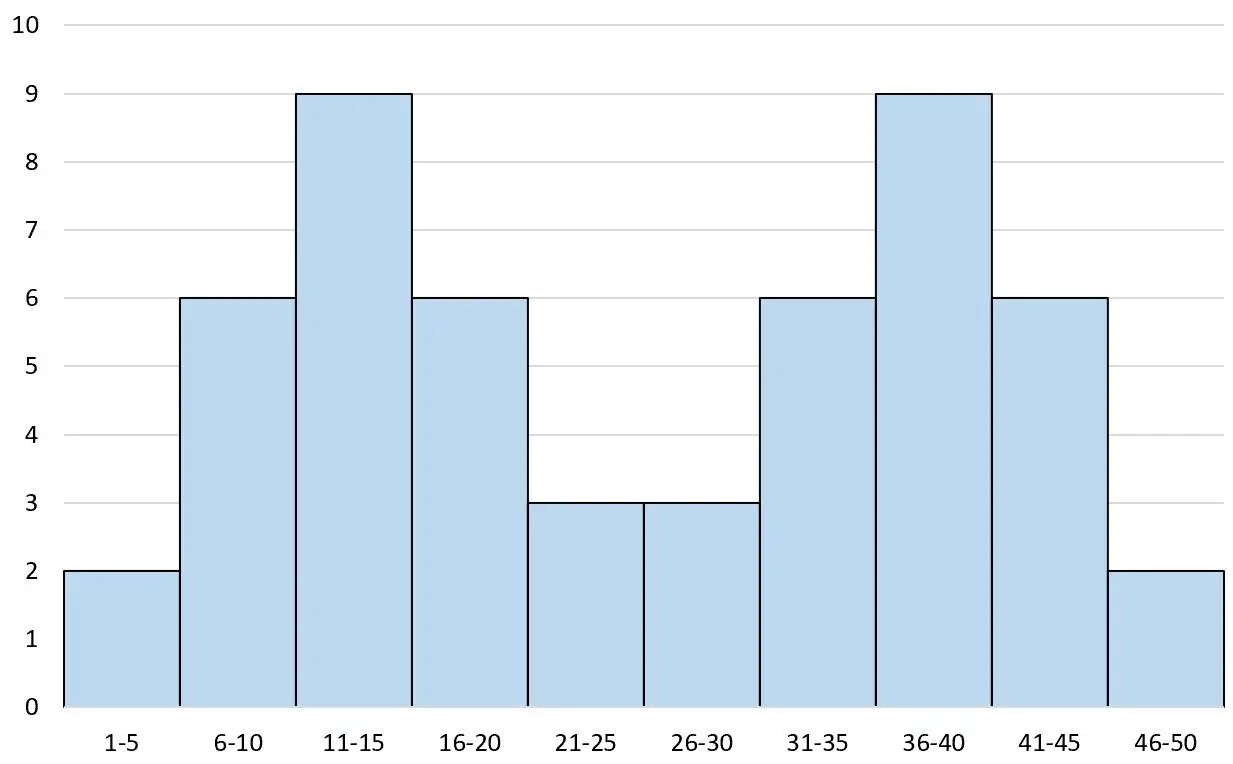
ဟီစတိုဂရမ်၏ အလယ်ဗဟိုတွင် မျဉ်းတစ်ကြောင်းဆွဲမည်ဆိုလျှင်၊ ဘယ်နှင့်ညာ နှစ်ဖက်သည် အတိအကျတူညီလိမ့်မည်-

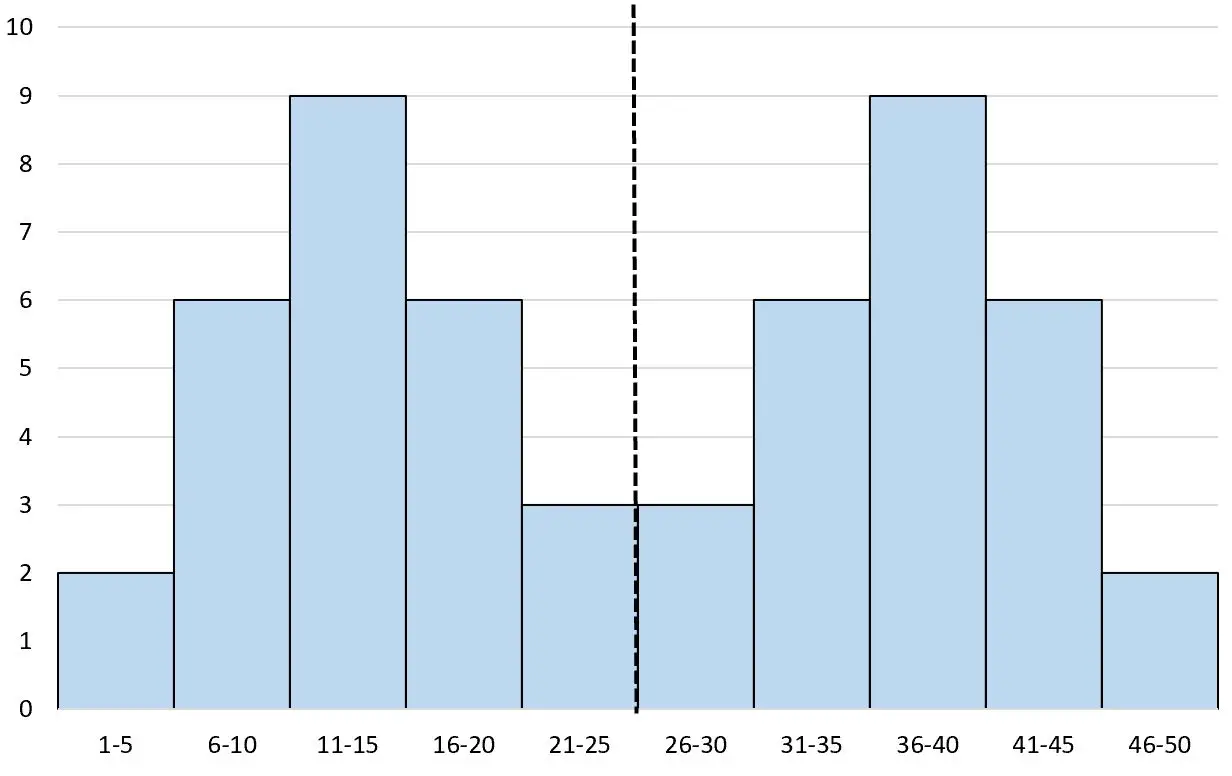
၎င်းကို bimodal symmetric histogram ဟုခေါ်သောကြောင့် “ bi” သည် ” two” ဖြစ်ပြီး ဤ histogram တွင် အထွတ်အထိပ်နှစ်ခုရှိသည်။

ဆက်စပ်- Bimodal Distributions မိတ်ဆက်

ခန့်မှန်းခြေ symmetrical histogram ဆိုတာဘာလဲ။

လက်တွေ့ကမ္ဘာတွင်၊ ပြီးပြည့်စုံသော အချိုးကျသော ဟစ်စတိုဂရမ်များ မရှိသလောက်နည်းသော်လည်း အကြမ်းဖျင်းအားဖြင့် အချိုးညီသော ဟစ်စတိုဂရမ်များ ရှိတတ်သည်။

ယင်းတို့သည် ဟစ်စတိုဂရမ်၏ အလယ်ဗဟိုတွင် မျဉ်းတစ်ကြောင်းဆွဲပါက နှစ်ဖက်စလုံးသည် အကြမ်းဖျင်းအားဖြင့် တူညီသည်ဟု ဆိုလိုသည်မှာ “ အကြမ်းဖျင်း” အချိုးကျသော ဟစ်စတိုဂရမ်များဖြစ်သည်။

ဥပမာတစ်ခုအနေနဲ့ မွေးကင်းစကလေးငယ်တွေရဲ့ ကိုယ်အလေးချိန်ကို ခွဲဝေပေးပါလိမ့်မယ်။

မွေးကင်းစကိုယ်အလေးချိန်သည် ပျမ်းမျှအားဖြင့် 7.5 ပေါင်ဖြင့် ပုံမှန်မဟုတ်သော ဖြန့်ဝေမှုနောက်တွင် ရှိကြောင်း ကောင်းစွာသိရှိထားသည်။

ကျွန်ုပ်တို့သည် ကလေးများ၏ ကိုယ်အလေးချိန်၏ ဟီစတိုဂရမ်ကို ဖန်တီးပါက၊ အချို့ကလေးငယ်များသည် ကိုယ်အလေးချိန်ပိုများပြီး အချို့သောကလေးများသည် ကိုယ်အလေးချိန် နည်းပါးသည့် 7.5 ပေါင်တွင် “ အထွတ်အထိပ်” ကို တွေ့ရမည်ဖြစ်ပါသည်။

ဤသည်မှာ အကြမ်းဖျင်း အချိုးကျသော ဟစ်စတိုဂရမ်တစ်ခုဖြစ်သည်။ အလယ်ဗဟိုကို ဒေါင်လိုက်မျဉ်းဆွဲလိုက်ရင် တစ်ဖက်စီက အကြမ်းဖျင်း အတူတူပါပဲ။

နောက်ထပ် ခိုင်မာသော ဥပမာတစ်ခုမှာ အမေရိကန်ပြည်ထောင်စုရှိ အထက်တန်းကျောင်းသူကျောင်းသားများအတွက် ACT ရမှတ်များ ဖြန့်ဝေခြင်း ဖြစ်သည်။

ပျမ်းမျှရမှတ်မှာ 21 ဝန်းကျင်ဖြစ်ပြီး အချို့သော ကျောင်းသားများတွင် အမှတ်နိမ့်ပြီး အခြားရမှတ်များ ပိုမိုမြင့်မားသည်။ အကယ်၍ ကျွန်ုပ်တို့သည် အမေရိကန်ပြည်ထောင်စုရှိ ကျောင်းသားအားလုံးအတွက် ACT ရမှတ်များ၏ ဟီစတိုဂရမ်ကို ဖန်တီးပါက၊ အချို့သော ကျောင်းသားများသည် အမှတ်ပိုမြင့်ပြီး အချို့သော ကျောင်းသားများသည် အမှတ်နိမ့်ခြင်းဖြင့် အသက် 21 နှစ်တွင် “ အထွတ်အထိပ်” တစ်ခုတည်းကို တွေ့ရလိမ့်မည်-

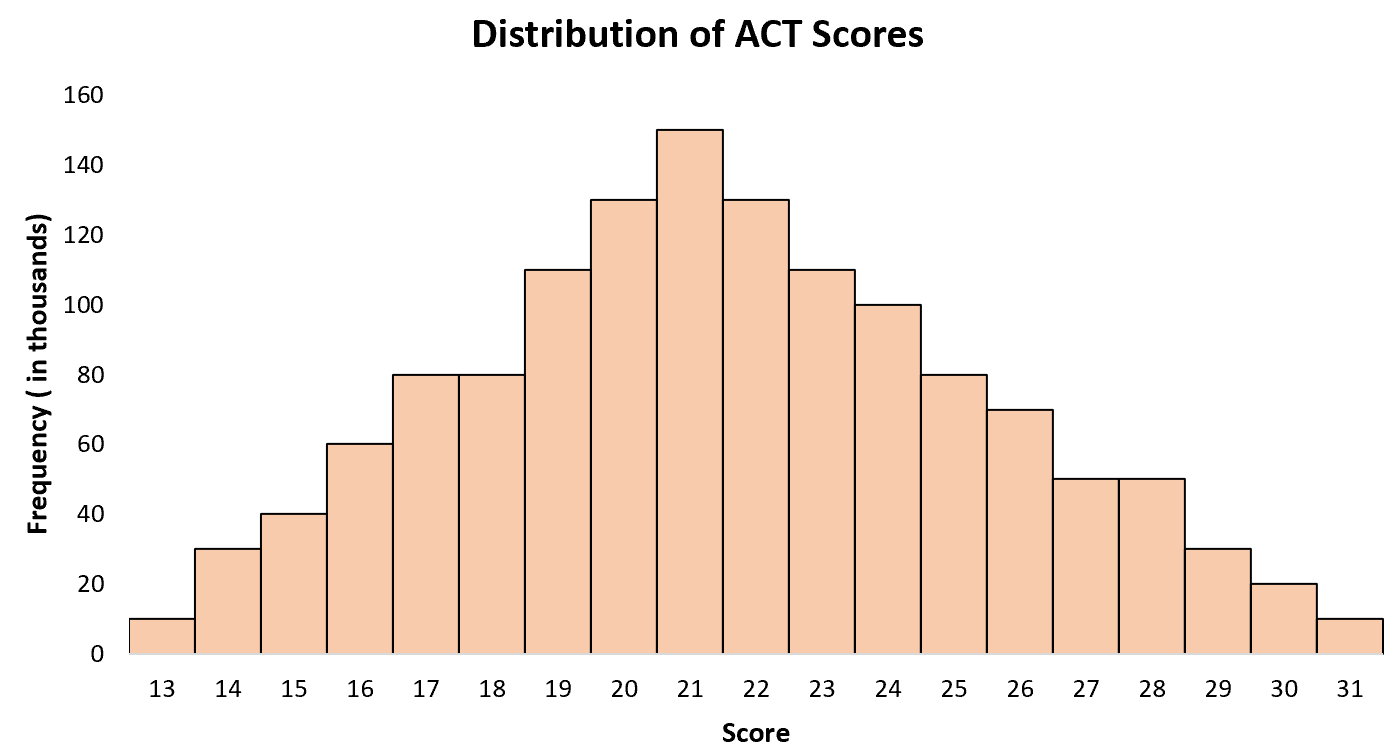
၎င်းသည် အကြမ်းဖျင်း အချိုးကျသည့် ဟစ်စတိုဂရမ်တစ်ခုလည်းဖြစ်သည်။ အလယ်ဗဟိုကို ဒေါင်လိုက်မျဉ်းဆွဲလိုက်ရင် တစ်ဖက်စီက အကြမ်းဖျင်း အတူတူပါပဲ။

real-world data sets တွေနဲ့ အလုပ်လုပ်တဲ့အခါ၊ ပြီးပြည့်စုံတဲ့ symmetrical histograms တွေကို တွေ့ရခဲပါတယ်၊ ဒါပေမယ့် အကြမ်းဖျင်းအားဖြင့် symmetrical histograms တွေကို ကြုံတွေ့ရတတ်ပါတယ်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် ဟီစတိုဂရမ်များအကြောင်း နောက်ထပ်အချက်အလက်များကို ပေးဆောင်သည်-

ဟစ်စတိုဂရမ်ပုံသဏ္ဍာန်ကို ဘယ်လိုဖော်ပြမလဲ။
ဟစ်စတိုဂရမ် နှိုင်းယှဉ်နည်း
ဟစ်စတိုဂရမ်တစ်ခု၏ ပျမ်းမျှနှင့် ပျမ်းမျှအား ခန့်မှန်းနည်း