အချိုးအစားအတွက် ယူဆချက် စမ်းသပ်ခြင်း။
ဤဆောင်းပါးသည် စာရင်းဇယားများတွင် မည်မျှသော hypothesis testing ဖြစ်သည်ကို ရှင်းပြထားသည်။ ထို့ကြောင့် အချိုးအစားအတွက် သီအိုရီစစ်ဆေးမှုအတွက် ဖော်မြူလာကို သင်တွေ့ရှိမည်ဖြစ်ပြီး ၎င်းကို မည်သို့လုပ်ဆောင်သည်ကို အပြည့်အဝနားလည်ရန် အဆင့်ဆင့် လေ့ကျင့်ခန်းတစ်ခုဖြစ်သည်။
အချိုးအစားအတွက် hypothesis test ဆိုတာဘာလဲ။
Proportion hypothesis testing သည် လူဦးရေအချိုးအစား၏ null hypothesis ကို ငြင်းပယ်ခြင်း ရှိ၊ မရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည့် ကိန်းဂဏန်းဆိုင်ရာ နည်းလမ်းတစ်ခုဖြစ်သည်။
ထို့ကြောင့်၊ အချိုးအစားနှင့် အရေးပါမှုအဆင့်အတွက် သီအိုရီစမ်းသပ်ကိန်းဂဏန်းတန်ဖိုးပေါ်မူတည်၍ null hypothesis ကို ပယ်ချခြင်း သို့မဟုတ် လက်ခံပါသည်။
သီအိုရီစမ်းသပ်ခြင်းအား တွေးခေါ်မှုဆန့်ကျင်ဘက်များ၊ သီအိုရီစမ်းသပ်ခြင်း သို့မဟုတ် အရေးပါမှုစမ်းသပ်ခြင်းဟုလည်း ခေါ်ဆိုနိုင်သည်ကို သတိပြုပါ။
အချိုးအစားအတွက် Hypothesis Testing Formula
အချိုးအစားအတွက် သီအိုရီစမ်းသပ်မှု ကိန်းဂဏန်းသည် နမူနာအချိုးအနုတ် အချိုးအစား၏ စံသွေဖည်မှုဖြင့် ပိုင်းခြားထားသော အချိုးအစား၏ အဆိုပြုတန်ဖိုးနှင့် ညီမျှသည်။
ထို့ကြောင့် အချိုးအစားအတွက် စမ်းသပ်မှုယူဆချက်ဖော်မြူလာ မှာ-

ရွှေ-
-

အချိုးအစားအတွက် hypothesis test statistic ဖြစ်ပါတယ်။
-

နမူနာအချိုးဖြစ်သည်။
-

အဆိုပြုထားသော အချိုးအစားတန်ဖိုးဖြစ်သည်။
-

နမူနာအရွယ်အစားဖြစ်သည်။
-

အချိုးအစား၏ စံသွေဖည်မှုဖြစ်သည်။
အချိုးအစားအတွက် သီအိုရီစမ်းသပ်မှု ကိန်းဂဏန်းကို တွက်ချက်ရန် မလုံလောက်ကြောင်း မှတ်သားထားပါ၊ သို့သော် ရလဒ်ကို အဓိပ္ပာယ်ဖွင့်ဆိုရပါမည်-
- အချိုးအစားအတွက် သီအိုရီစမ်းသပ်မှုမှာ နှစ်ဖက်သဘောတူပါက၊ စာရင်းအင်း၏ ပကတိတန်ဖိုးသည် အရေးကြီးသောတန်ဖိုး Z α/2 ထက်ကြီးပါက null hypothesis ကို ပယ်ချပါသည်။
- အချိုးအစားအတွက် သီအိုရီစစ်ဆေးမှုသည် မှန်ကန်သောအမြီးနှင့်ကိုက်ညီပါက၊ ကိန်းဂဏာန်းသည် အရေးကြီးသောတန်ဖိုး Z α ထက်ကြီးပါက null hypothesis ကို ပယ်ချပါသည်။
- အချိုးအစားအတွက် သီအိုရီစစ်ဆေးမှုသည် ဘယ်ဘက်အမြီးနှင့် ကိုက်ညီပါက၊ ကိန်းဂဏန်းသည် အရေးကြီးသောတန်ဖိုး -Z α ထက်နည်းပါက null hypothesis ကို ပယ်ချပါသည်။
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: p\neq p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: p> p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: p< p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7d5bd583532769e3014286e8ffd94c9f_l3.png)
အရေးကြီးသောတန်ဖိုးများကို ပုံမှန်ဖြန့်ဝေဇယားမှ အလွယ်တကူ ရယူနိုင်ကြောင်း သတိရပါ။
အချိုးအစားအတွက် Hypothesis Testing နမူနာ
အချိုးအစားအတွက် သီအိုရီစမ်းသပ်ခြင်း၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ၎င်း၏ဖော်မြူလာသည် အဘယ်အရာဖြစ်သည်ကို ကျွန်ုပ်တို့မြင်သည်နှင့် သဘောတရားကို ပိုမိုနားလည်ရန် ဥပမာတစ်ခုကို ကျွန်ုပ်တို့ဖြေရှင်းပါမည်။
- ၎င်း၏ထုတ်လုပ်သူအဆိုအရ သီးခြားရောဂါတစ်ခုကို တိုက်ဖျက်သည့်ဆေးသည် 70% ထိရောက်သည်။ ဓာတ်ခွဲခန်းတွင်၊ သုတေသီများက အချိုးအစား ကွဲပြားသည်ဟု ယုံကြည်သောကြောင့် ဤဆေး၏ ထိရောက်မှုကို စမ်းသပ်ပါသည်။ ယင်းအတွက် ဆေးကို လူနာ ၁၀၀၀ ၏နမူနာတွင် စမ်းသပ်ပြီး လူ ၆၄၁ ဦး သက်သာပျောက်ကင်းခဲ့သည်။ သုတေသီများ၏ ယူဆချက်အား ငြင်းပယ်ခြင်း သို့မဟုတ် မပြုရန် သိသိသာသာ အဆင့် 5% ရှိသော လူဦးရေအချိုးအပေါ် သီအိုရီစစ်ဆေးမှုကို ပြုလုပ်ပါ။
ဤကိစ္စတွင်၊ လူဦးရေအချိုးအစားအတွက် သီအိုရီစမ်းသပ်မှု၏ null hypothesis နှင့် အခြား hypothesis တို့သည်-
![Rendered by QuickLaTeX.com \begin{cases}H_0: p=0,70\\[2ex] H_1:p\neq 0,70 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f7da8281eeecc022e2ec7daea6a9756e_l3.png)
ဆေးဝါးဖြင့် ပျောက်ကင်းအောင် ကုသခဲ့သော နမူနာများတွင် လူအချိုးအစားမှာ-
![]()
အထက်ဖော်ပြပါ ဖော်မြူလာကို အသုံးပြုခြင်းဖြင့် အချိုးအစားအတွက် သီအိုရီစစ်ဆေးမှု ကိန်းဂဏန်းကို ကျွန်ုပ်တို့ တွက်ချက်သည်-
![Rendered by QuickLaTeX.com \begin{aligned} \displaystyle Z&=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}\\[2ex]Z&=\frac{0,641-0,70}{\displaystyle\sqrt{\frac{0,70\cdot (1-0,70)}{1000}}} \\[2ex] Z&=-4,07\end{aligned}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e689388b0a73e91c1e3d8812c2c4c42a_l3.png)
အခြားတစ်ဖက်တွင်၊ သိသာထင်ရှားမှုအဆင့်မှာ 0.05 ဖြစ်ပြီး ၎င်းသည် အမြီးနှစ်ပိုင်းဆိုင်ရာ ယူဆချက်စမ်းသပ်မှုဖြစ်သောကြောင့်၊ စမ်းသပ်မှု၏ အရေးကြီးသောတန်ဖိုးမှာ 1.96 ဖြစ်သည်။
![]()
နိဂုံးချုပ်အားဖြင့်၊ စစ်ဆေးမှုစာရင်းအင်း၏ ပကတိတန်ဖိုးသည် အရေးကြီးသောတန်ဖိုးထက် ကြီးသောကြောင့် ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းပယ်ပြီး အစားထိုးယူဆချက်အား လက်ခံပါသည်။
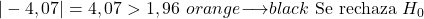 ➤ ဆိုလိုရင်းအတွက် သဘောတရားကို စမ်းသပ် ကြည့်ပါ။
➤ ဆိုလိုရင်းအတွက် သဘောတရားကို စမ်းသပ် ကြည့်ပါ။
နမူနာအချိုးအစားနှစ်ခုအတွက် ယူဆချက်စမ်းသပ်ခြင်း။
နမူနာနှစ်ခု၏ အချိုးအစားအတွက် တွေးခေါ်မှုစမ်းသပ်ခြင်းကို ကွဲပြားသော လူဦးရေနှစ်ခု၏ အချိုးအစားသည် ညီမျှသည်ဟူသော null hypothesis ကို ငြင်းပယ်ရန် သို့မဟုတ် လက်ခံရန် အသုံးပြုသည်။
ထို့ကြောင့်၊ နမူနာအချိုးအစားနှစ်ခုအတွက် hypothesis test ၏ null hypothesis သည် အမြဲတမ်းဖြစ်သည်-
![]()
အစားထိုးယူဆချက်သည် ရွေးချယ်စရာ သုံးခုထဲမှ တစ်ခု ဖြစ်နိုင်သော်လည်း၊
*** QuickLaTeX cannot compile formula:
\begin{array}{l}H_1:p_1\neq p_2\\[2ex]H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio of the two samples is calculated as follows:[latex]p=\cfrac {x_1+x_2}{n_1+n_2}
*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ...H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio
Please use \mathaccent for accents in math mode.
leading text: ...\[2ex]H_1:p_1 The combined ratio of the two
Please use \mathaccent for accents in math mode.
leading text: ...combined of the two samples is calculated
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
နမူနာအချိုးအစားနှစ်ခုအတွက် သီအိုရီစမ်းသပ်ကိန်းဂဏန်းကို တွက်ချက်ရန် ဖော်မြူလာမှာ-
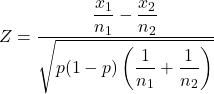
ရွှေ-
-

နမူနာအချိုးအစားနှစ်ခုအတွက် သီအိုရီစမ်းသပ်မှု ကိန်းဂဏန်းဖြစ်သည်။
-
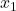
နမူနာ 1 တွင် ရလဒ်အရေအတွက်ဖြစ်သည်။
-
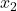
နမူနာ 2 တွင် ရလဒ်အရေအတွက်ဖြစ်သည်။
-

နမူနာအရွယ်အစား 1 ဖြစ်ပါတယ်။
-

နမူနာအရွယ်အစား 2 ဖြစ်ပါတယ်။
-

နမူနာနှစ်ခု၏ ပေါင်းစပ်အချိုးအစားဖြစ်သည်။
k နမူနာအချိုးအစားအတွက် သီအိုရီစမ်းသပ်ခြင်း။
k နမူနာများ၏ အချိုးအစားများနှင့် ပတ်သက်သော ယူဆချက် စမ်းသပ်မှု တွင် ရည်မှန်းချက်မှာ မတူညီသော လူဦးရေ၏ အချိုးအစားများအားလုံး တူညီခြင်း ရှိ၊ ထို့ကြောင့်၊ ဤကိစ္စရပ်တွင် null hypothesis နှင့် အခြား hypothesis တို့သည်-
![Rendered by QuickLaTeX.com \begin{cases}H_0: \text{Todas las proporciones son iguales}\\[2ex] H_1: \text{No todas las proporciones son iguales} \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-77d7e13b427dd927953473a6bfbe9a55_l3.png)
ဤကိစ္စတွင်၊ နမူနာအားလုံး၏ ပေါင်းစပ်အချိုးအစားကို အောက်ပါအတိုင်း တွက်ချက်သည်။
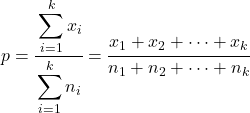
k နမူနာအချိုးအစားအတွက် သီအိုရီစမ်းသပ်မှု ကိန်းဂဏန်းကို ရှာဖွေရန် ဖော်မြူလာမှာ-
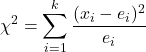
![]()
ရွှေ-
-

k နမူနာအချိုးအစားအတွက် သီအိုရီစမ်းသပ်မှု ကိန်းဂဏန်းတစ်ခုဖြစ်သည်။ ဤကိစ္စတွင်၊ ကိန်းဂဏန်းသည် chi-square ဖြန့်ဝေမှုနောက်တွင်ဖြစ်သည်။
-

နမူနာ i တွင် ရလဒ်အရေအတွက်ဖြစ်သည်။
-

နမူနာအရွယ်အစား i ဖြစ်ပါတယ်။
-

နမူနာအားလုံး၏ အချိုးအစားဖြစ်သည်။
-

နမူနာ i မှ မျှော်လင့်ထားသော hit အရေအတွက်ဖြစ်သည်။ ပေါင်းစပ်အချိုးအစားကို မြှောက်ခြင်းဖြင့် တွက်ချက်သည်။

နမူနာအရွယ်အစားအားဖြင့်

.