အခြေအနေအရ ဖြစ်နိုင်ခြေ (သို့မဟုတ် အခြေအနေအရ ဖြစ်နိုင်ခြေ)

အားဖြင့် ဩဂုတ် 6, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤနေရာတွင် အခြေအနေဆိုင်ရာ ဖြစ်နိုင်ခြေ (သို့မဟုတ် အခြေအနေဆိုင်ရာ ဖြစ်နိုင်ခြေ) ဟူသည်ကို သင်တွေ့လိမ့်မည်။ ဥပမာတစ်ခုနှင့် ဤဖြစ်နိုင်ခြေအမျိုးအစား၏ ဂုဏ်သတ္တိများဖြင့် အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေကို တွက်ချက်ပုံကို ရှင်းပြပါသည်။ ထို့အပြင်၊ အဆင့်ဆင့်ဖြေရှင်းထားသော အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေလေ့ကျင့်ခန်းများဖြင့် လေ့ကျင့်နိုင်မည်ဖြစ်သည်။

အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေကဘာလဲ။

Conditional probability ၊ conditional probability ဟုခေါ်သည် ၊ သည် အခြား event B ဖြစ်ပေါ်လာပါက event A ဖြစ်ပေါ်လာမည့် ဖြစ်နိုင်ခြေကို ညွှန်ပြသည့် ကိန်းဂဏန်းဆိုင်ရာ တိုင်းတာမှုတစ်ခုဖြစ်သည်။ ဆိုလိုသည်မှာ၊ အခြေအနေအရဖြစ်နိုင်ခြေ P(A|B) သည် ဖြစ်ရပ် B ဖြစ်ပေါ်လာပြီးနောက် ဖြစ်ရပ် A ၏ ဖြစ်နိုင်ခြေကို ရည်ညွှန်းသည်။

အခြေအနေအရဖြစ်နိုင်ခြေကို ဖြစ်ရပ်နှစ်ခုကြားရှိ ဒေါင်လိုက်ဘားတစ်ခုဖြင့် ရေးသားထားသည်- P(A|B) သည်- “ ဖြစ်ရပ် A ပေးထားသည့် ဖြစ်ရပ် B” ၏ အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေကို ဖတ်သည်။

အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေတန်ဖိုးသည် 0 နှင့် 1 အကြား နံပါတ်တစ်ခုဖြစ်ကြောင်း သတိပြုပါ။ အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေပိုများလေ၊ ဖြစ်ရပ် B ဖြစ်ပေါ်လာသည့်အခါ ဖြစ်ရပ် A ဖြစ်ပေါ်လာနိုင်ခြေ ပိုများသော်လည်း အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေ နည်းပါးလေ၊ ထိုဖြစ်ရပ် A ဖြစ်နိုင်ခြေနည်းလေလေ၊ Event B ဖြစ်ပေါ်လာတဲ့အခါ ဖြစ်ပေါ်လာလိမ့်မယ်။

အခြေအနေအရ ဖြစ်နိုင်ခြေ ဖော်မြူလာ

ဖြစ်ရပ် A ၏အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေသည် ဖြစ်ရပ် B ၏ ဖြစ်နိုင်ခြေဖြင့် ပိုင်းခြားထားသော ဖြစ်ရပ် A နှင့် ဖြစ်ရပ် B ကြားလမ်းဆုံဖြစ်နိုင်ခြေနှင့် ညီမျှသည်။

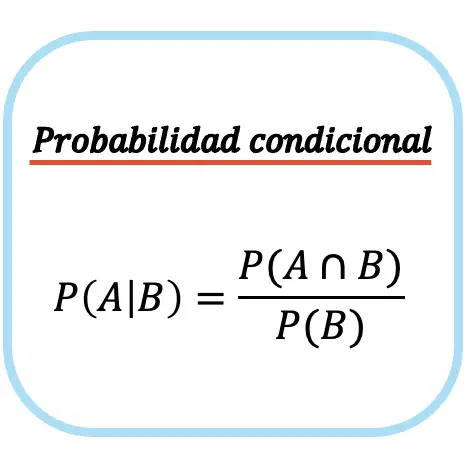
အခြေအနေအရ သို့မဟုတ် အခြေအနေအရ ဖြစ်နိုင်ခြေ

အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေ (သို့မဟုတ် အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေ) ဖော်မြူလာကို ခြွင်းချက်မရှိဖြစ်ရပ်၏ဖြစ်နိုင်ခြေသည် သုညမဟုတ်သော၊ ဆိုလိုသည်မှာ P(B)≠0 သာဖြစ်နိုင်သည်ကို သတိပြုပါ။ သို့မဟုတ် တစ်နည်းအားဖြင့် အဖြစ်အပျက် B ဖြစ်ပေါ်လာနိုင်လျှင်။

P(B|A) ကို သိရှိပါက၊ P(A|B) ကို ၎င်း၏ပြောင်းပြန်မှ တွက်ချက်နိုင်သည်။ ဒါပေမယ့် ဒါကိုလုပ်ဖို့ သင် Bayes ရဲ့ သီအိုရီကို အသုံးချရမှာဖြစ်ပြီး၊ ဒီသီအိုရီက ဘာပါ၀င်လဲဆိုတာကို ဒီမှာ ကြည့်နိုင်ပါတယ်။

Conditional Probability ၏ ဥပမာ

အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ပုံသေနည်းကို ကျွန်ုပ်တို့တွေ့မြင်ပြီးသည်နှင့် ၎င်း၏အဓိပ္ပာယ်ကို အပြည့်အဝနားလည်ရန် ဤဖြစ်နိုင်ခြေအမျိုးအစား၏ ဥပမာတစ်ခုကို တစ်ဆင့်ပြီးတစ်ဆင့် ဖြေရှင်းပါမည်။

  • ကျောင်းသား 30 ရှိသောအတန်းတွင် စာမေးပွဲဖြေဆိုပြီးနောက် ကျောင်းသားမည်မျှလေ့လာပြီး မည်မျှအောင်မြင်သည်ကို သိရှိရန် အချက်အလက်များကို စုဆောင်းခဲ့သည်။ ရလဒ်များကို အောက်ပါ အရေးပေါ်ဇယားတွင် ဖော်ပြထားပါသည်။ စုဆောင်းထားသောဒေတာမှ၊ သင်လေ့လာပြီးပါက စာမေးပွဲဖြေဆိုရမည့် ဖြစ်နိုင်ခြေကို တွက်ချက်ပါ။
conditional probability လေ့ကျင့်ခန်းကို ဖြေရှင်းထားသည်။

အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေကို ရယူရန်၊ ကျွန်ုပ်တို့သည် ယခင်က ကျွန်ုပ်တို့မြင်ခဲ့သည့် ဖော်မြူလာကို အသုံးပြုရပါမည်-

P(\text{aprobado}|\text{estudiado})=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}

ထို့ကြောင့်၊ ကျောင်းသားတစ်ဦးသည် လေ့လာဆည်းပူးလေ့လာပြီး အောင်မြင်သွားသည့် ဖြစ်နိုင်ခြေကို ဦးစွာရှာဖွေရန် လိုအပ်ပါသည်။ ကျောင်းသားတစ်ဦးလေ့လာခဲ့သည့်ဖြစ်နိုင်ခြေကိုရှာဖွေရန် Laplace ၏စည်းမျဉ်းကိုရိုးရှင်းစွာအသုံးပြုရန်လိုအပ်သည်၊ ဆိုလိုသည်မှာ၊ လေ့လာသူစုစုပေါင်းအရေအတွက်ဖြင့်လေ့လာသောကျောင်းသားအရေအတွက်ကိုပိုင်းခြားသည်-

P(\text{estudiado})=\cfrac{23}{30}=0,77

ထို့အပြင် ကျောင်းသားတစ်ဦး လေ့လာပြီး အောင်မြင်သွားသော ကျောင်းသားအရေအတွက်ကို စုစုပေါင်းဖြင့် ပိုင်းခြားခြင်းဖြင့် အရေးပေါ်ဇယားမှ တစ်ချိန်တည်းတွင် ဖြေဆိုနိုင်သည်-

P(\text{aprobado}\cap \text{estudiado})=\cfrac{19}{30}=0,63

ထို့ကြောင့် ကျောင်းသားတစ်ဦးသည် စာမေးပွဲအောင်လျှင် ဖြစ်နိုင်ခြေမှာ-

\begin{aligned}P(\text{aprobado}|\text{estudiado})&=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}\\ &=\cfrac{0,63}{0,77}\\[1.5ex] &=0,82\end{aligned}

မှီခိုမှုနှင့် အမှီအခိုကင်းသော ဖြစ်ရပ်များ၏ အခြေအနေအရ ဖြစ်နိုင်ခြေ

ဤကဏ္ဍတွင် အခြေအနေဆိုင်ရာ ဖြစ်နိုင်ခြေနှင့် မှီခိုမှုနှင့် အမှီအခိုကင်းသော ဖြစ်ရပ်များ (သို့မဟုတ် မှီခိုမှုနှင့် အမှီအခိုကင်းသော ဖြစ်ရပ်များ) အကြား ဆက်နွယ်မှုကို ကျွန်ုပ်တို့ မြင်တွေ့ရပါမည်။ အဘယ်ကြောင့်ဆိုသော် ၎င်းတို့သည် မတူညီသော အယူအဆများဖြစ်သော်လည်း၊ ဤဖြစ်ရပ်နှစ်မျိုးသည် အခြေအနေအရ ဖြစ်နိုင်ခြေနှင့် ဆက်စပ်နေသောကြောင့်ဖြစ်သည်။

အဖြစ်အပျက်နှစ်ခု (သို့မဟုတ် ဖြစ်ပျက်မှု) သည် တစ်ခုနှင့်တစ်ခုအပေါ်တွင်မူတည်ခြင်းမရှိသောအခါ ၎င်းတို့၏ဖြစ်ပျက်နိုင်ခြေသည် သီးခြားဖြစ်သည်။ ထိုသို့သော အခြေအနေမျိုးတွင်၊ ဖြစ်ရပ်နှစ်ခုကြား ဆုံစည်းမှုသည် သီးခြားစီဖြစ်နိုင်ခြေ၏ ရလဒ်နှင့် ညီမျှသည်။ ထို့ကြောင့်၊ အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေဖော်မြူလာကို ရိုးရှင်းအောင်ပြုလုပ်ထားသည်-

P(A|B)=\cfrac{P(A\cap B)}{P(B)}=\cfrac{P(A)\cdot P(B)}{P(B)}=P(A)

အတိုချုပ် အားဖြင့်၊ ဖြစ်ရပ် A နှင့် B သည် သီးခြားလွတ်လပ်ပါက၊ ဖြစ်ရပ် A ပေးထားသည့် အဖြစ်အပျက် B ၏ အခြေအနေအရ ဖြစ်နိုင်ခြေသည် အဖြစ်အပျက် A ဖြစ်ပျက်မှု ဖြစ်နိုင်ခြေနှင့် အတိအကျ တူညီပါသည်။

တစ်ဖက်တွင်၊ ဖြစ်ရပ်နှစ်ခုကို မှီခိုနေသောအခါ၊ ဖြစ်ရပ်တစ်ခု၏ ဖြစ်နိုင်ခြေသည် အခြားဖြစ်ရပ်၏ ဖြစ်နိုင်ခြေအပေါ် မူတည်သည်ဟု ဆိုလိုသည်။ ထို့ကြောင့် ဖြစ်ရပ်နှစ်ခု A နှင့် B ကို မှီခိုသောအခါ၊ ဖြစ်ရပ် A ပေးထားသည့် အဖြစ်အပျက် B ၏ အခြေအနေအရ ဖြစ်နိုင်ခြေသည် အဖြစ်အပျက် A ၏ ဖြစ်ပျက်နိုင်ခြေနှင့် ကွဲပြားသည်။

P(A|B)\neq P(A)

အခြေအနေအရ ဖြစ်နိုင်ခြေ လေ့ကျင့်ခန်းများကို ဖြေရှင်းခဲ့သည်။

လေ့ကျင့်ခန်း ၁

ဘောလုံးများပြည့်နေသော အိတ်တစ်လုံးတွင် တစ်ဝက်သည် လိမ္မော်ရောင်ဖြစ်ပြီး ကျန်တစ်ဝက်မှာ အစိမ်းရောင်ဖြစ်ကြောင်း ကျွန်ုပ်တို့သိသည်။ ထို့အပြင် ဘောလုံးအားလုံး၏ သုံးပုံတစ်ပုံသည် လိမ္မော်ရောင်ဖြစ်ပြီး တစ်ချိန်တည်းတွင် အမှတ်အသားပြုထားသည်။ လိမ္မော်ရောင်ဘောလုံးကိုဆွဲသည့်အခါ ၎င်းသည် signal ကိုလက်ခံရရှိမည့်ဖြစ်နိုင်ခြေအဘယ်နည်း။

လေ့ကျင့်ခန်းကိုဖြေရှင်းရန်၊ ကျွန်ုပ်တို့သည် အခြေအနေအလိုက် ဖော်မြူလာဖြစ်နိုင်ခြေကို အသုံးပြုရမည်ဖြစ်ပြီး၊

P(\text{se\~nal}|\text{naranja})=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}

ပြဿနာထုတ်ပြန်ချက်တွင် အိတ်တစ်ဝက်သည် လိမ္မော်သီးဖြစ်ကြောင်း ဖော်ပြထားသည်။ ထို့ကြောင့် လိမ္မော်သီးတစ်လုံးကို ကောက်ခြင်း၏ သီအိုရီအရ ဖြစ်နိုင်ခြေမှာ 50% ဖြစ်သည်။

P(\text{naranja})=\cfrac{1}{2}=0,5

အခြားတစ်ဖက်တွင်၊ စုစုပေါင်း၏သုံးပုံတစ်ပုံသည် လိမ္မော်ရောင်ဘောလုံးများဖြစ်ပြီး အချက်ပြမှုရှိကြောင်း ကျွန်ုပ်တို့သိထားသောကြောင့် လိမ္မော်ဘောလုံးတစ်လုံးကို အချက်ပြခြင်းဖြင့် ရရှိနိုင်ခြေမှာ-

P(\text{se\~nal}\cap \text{naranja})=\cfrac{1}{3}=0,33

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် ၎င်း၏တန်ဖိုးကိုရှာဖွေရန် တွက်ချက်ထားသော ဖြစ်နိုင်ခြေများကို အခြေအနေဆိုင်ရာ ဖြစ်နိုင်ခြေဖော်မြူလာဖြင့် အစားထိုးသည်-

\begin{aligned}P(\text{se\~nal}|\text{naranja})&=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}\\ &=\cfrac{0,33}{0,5}\\[1.5ex] &=0,66\end{aligned}

အချုပ်အားဖြင့်ဆိုရသော် ၎င်းသည် လိမ္မော်ရောင်ဖြစ်ပါက အချက်ပြဘောလုံးတစ်ခုဆွဲရန် ဖြစ်နိုင်ခြေမှာ 66% ဖြစ်သည်။

လေ့ကျင့်ခန်း ၂

အကယ်၍ ကျွန်ုပ်တို့တွင် အပြာရောင်ဘောပင်ခြောက်ချောင်းနှင့် အနက်ရောင်ဘောပင်သုံးချောင်းရှိလျှင် အပြာရောင်ဘောပင်တစ်ချောင်းဆွဲရန် ဖြစ်နိုင်ခြေနှင့် အပြာရောင်ဘောပင်နှစ်ချောင်းကို ရှေ့ဆင့်နောက်ဆင့် ရေးဆွဲနိုင်ခြေကို တွက်ချက်ပါ။

အပြာရောင်ဘောပင်ကို တစ်ကြိမ် ကောက်ယူနိုင်ခြေကို ဆုံးဖြတ်ရန် Laplace ၏ ဥပဒေ ကို အသုံးပြုပါ-

P(\text{azul})=\cfrac{6}{6+3}=0,67

ပြဿနာက အပြာရောင်ဘောပင်နှစ်ချောင်းကို ရှေ့ဆင့်နောက်ဆင့် ကောက်ယူနိုင်ခြေကို သိစေသည်၊ ဆိုလိုသည်မှာ အကယ်၍ ကျွန်ုပ်တို့သည် ယခင်က အပြာရောင်ဘောပင်ကို ကောက်ယူပြီးပါက အပြာရောင်ဘောပင်ကို ကောက်ယူနိုင်သည့် အခြေအနေရှိနိုင်ခြေကိုလည်း သိရှိရန် တောင်းဆိုပါသည်။

အပြာရောင်ဘောပင်ကိုဆွဲလျှင် ကျွန်ုပ်တို့တွင် အဆင်သင့်နည်းသော ကိစ္စတစ်ခုရှိသော်လည်း စုစုပေါင်းတွင် ဘောပင်တစ်ချောင်းလည်း လျော့နည်းပါသည်။ ထို့ကြောင့် အခြေအနေအရ ဖြစ်နိုင်ခြေမှာ-

P(\text{azul}|\text{azul})=\cfrac{5}{8}=0,63

လေ့ကျင့်ခန်း ၃

အကြွေစေ့ပစ်ခြင်းသည် ခေါင်းကို ဖြစ်ပေါ်စေသည့် နံပါတ် 4 သို့ သေတ္တာကို လှိမ့်ခြင်း၏ အခြေအနေအရ ဖြစ်နိုင်ခြေမှာ အဘယ်နည်း။

ဤလေ့ကျင့်ခန်းကိုဖြေရှင်းရန်၊ အခြေအနေအရဖြစ်နိုင်ခြေ သီအိုရီကို ထည့်သွင်းစဉ်းစားရမည်ဖြစ်ပြီး၊ အကြောင်းမှာ ဖြစ်ရပ်များသည် “ အသေခံပစ်ခြင်းဖြင့် နံပါတ် ၄ ကိုရယူခြင်း” နှင့် “ ဒင်္ဂါးပြားပစ်ခြင်းဖြင့် ဦးခေါင်းများရယူခြင်း” တို့သည် သီးခြားဖြစ်သောကြောင့် ဖြစ်သည်။ ထို့ကြောင့် အခြေအနေအလိုက် ဖြစ်နိုင်ခြေဖော်မြူလာကို အသုံးပြုရန် မလိုအပ်သော်လည်း အောက်ပါ တန်းတူညီမျှမှုကို ကျေနပ်သည်-

P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})

ထို့ကြောင့်၊ အခြေအနေအရဖြစ်နိုင်ခြေကိုရှာဖွေရန် Laplace ၏စည်းမျဉ်းကိုရိုးရှင်းစွာအသုံးပြုပါ။

P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})=\cfrac{1}{6}=0,167

လေ့ကျင့်ခန်း ၄

နိုင်ငံတစ်နိုင်ငံရှိ ကုမ္ပဏီ ၂၅ ခု၏ ဘဏ္ဍာရေးနှစ်ကို လေ့လာပြီး ယခုနှစ်၏ စီးပွားရေးရလဒ်ပေါ်မူတည်၍ ၎င်းတို့၏ စတော့စျေးနှုန်းများ မည်ကဲ့သို့ ပြောင်းလဲသွားသည်ကို လေ့လာခဲ့သည်။ အောက်ပါ အရေးပေါ်ဇယားတွင် စုဆောင်းထားသော ဒေတာကို သင်တွေ့မြင်နိုင်သည်-

conditional probability လေ့ကျင့်ခန်းကို ဖြေရှင်းထားသည်။

ကုမ္ပဏီတစ်ခု၏ စတော့ဈေးသည် လွန်ခဲ့သည့်နှစ်တွင် အမြတ်ရခဲ့လျှင် မည်မျှမြင့်တက်နိုင်မည်နည်း။

လေ့ကျင့်ခန်းသည် ကုမ္ပဏီသည် အပြုသဘောဆောင်သော စီးပွားရေးရလဒ်ကို ရရှိသောကြောင့် စတော့ရှယ်ယာများ မြင့်တက်လာမည့် အခြေအနေအကြောင်း ကျွန်ုပ်တို့ကို မေးသည်။ ထို့ကြောင့်၊ ဤဖြစ်နိုင်ခြေကို တွက်ချက်ရန်၊ အခြေအနေဆိုင်ရာ ဖြစ်နိုင်ခြေဖော်မြူလာကို အသုံးပြုရပါမည်-

P(\text{precio sube}|\text{beneficio})=\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}

ထို့ကြောင့် ကုမ္ပဏီတစ်ခုသည် အမြတ်အစွန်းရနိုင်သည့် ဖြစ်နိုင်ခြေကို ဦးစွာတွက်ချက်ပြီး ဒုတိယအချက်မှာ ကုမ္ပဏီတစ်ခုသည် ရှယ်ယာတစ်ခုလျှင် ၎င်း၏စျေးနှုန်းကို တိုးစေပြီး စီးပွားရေးအမြတ်အစွန်းရနိုင်ခြေကို တွက်ချက်ပါသည်။

P(\text{beneficio})=\cfrac{14}{25}=0,56

P(\text{precio sube}\cap\text{beneficio})=\cfrac{10}{25}=0,4

ထို့နောက် ကျွန်ုပ်တို့သည် တွေ့ရှိသောတန်ဖိုးများကို ဖော်မြူလာတွင် အစားထိုးပြီး အခြေအနေဆိုင်ရာ ဖြစ်နိုင်ခြေကို တွက်ချက်သည်-

\begin{aligned}P(\text{precio sube}|\text{beneficio})& =\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}\\ &= \cfrac{0,4}{0,56}\\[1.5ex]& =0,71 \end{aligned}

အခြေအနေအရ ဖြစ်နိုင်ခြေ၏ ဂုဏ်သတ္တိများ

အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေ သို့မဟုတ် အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေ၏ ဂုဏ်သတ္တိများမှာ အောက်ပါအတိုင်းဖြစ်သည်-

  • အဖြစ်အပျက် A ၏ အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေ၏ ပေါင်းလဒ်သည် A ပေးထားသည့် အဖြစ်အပျက် B နှင့် ပေါင်းစပ်ဖြစ်ရပ် A ၏ အခြေအနေဆိုင်ရာဖြစ်နိုင်ခြေ ပေါင်းလဒ်သည် ပေးထားသည့် အဖြစ်အပျက် B သည် တစ်ခုနှင့် ညီမျှသည်။

P\bigl(A|B\bigr)+P\bigl(\overline{A}|B\bigr)=1

  • အကယ်၍ ဖြစ်ရပ် A သည် ဖြစ်ရပ် B ၏ အစုခွဲတစ်ခုဖြစ်ပါက၊ A သည် B သည် အမှန်ဖြစ်သောအခါ အမြဲတမ်း ဖြစ်ပေါ်နေလိမ့်မည်။ ထို့ကြောင့်၊ ဤကိစ္စများတွင် အဖြစ်အပျက် A ၏ အခြေအနေအရ ဖြစ်နိုင်ခြေသည် 1 ဖြစ်သည်။

B\subseteq A \ \longrightarrow \ P(A|B)=1

  • မတူညီသော ဖြစ်ရပ်နှစ်ခုကြောင့်၊ အခြေအနေအရဖြစ်နိုင်ခြေနှင့်စပ်လျဉ်း၍ အောက်ပါ တန်းတူညီမျှမှုသည် အမြဲတမ်းရှိနေသည်-

P\bigl(A\bigr)=P\bigl(A|B\bigr)\cdot P\bigl(B\bigr)+P\bigl(A|\overline{B}\bigl)\cdot P\bigl(\overline{B}\bigr)

စာရေးသူအကြောင်း

Benjamin Anderson
Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။

မှတ်ချက်တစ်ခုထည့်ပါ။

သင့် email လိပ်စာကို ဖော်ပြမည် မဟုတ်ပါ။ လိုအပ်သော ကွက်လပ်များကို * ဖြင့်မှတ်သားထားသည်