R တွင် brown–forsythe စမ်းသပ်မှု- အဆင့်ဆင့် ဥပမာ

တစ်လမ်းသွား ANOVA ကို သုံးသော သို့မဟုတ် ထို့ထက်မကသော သီးခြားအုပ်စုများ၏ နည်းလမ်းများကြား သိသာထင်ရှားသော ခြားနားမှု ရှိ၊ မရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည်။

တစ်လမ်းသွား ANOVA ၏ ယူဆချက် တစ်ခုသည် နမူနာများကို ထုတ်ယူသည့် လူဦးရေ၏ ကွဲလွဲမှုများသည် တူညီသည်ဟု ဆိုသည်။

၎င်းကိုစမ်းသပ်ရန် အသုံးအများဆုံးနည်းလမ်းတစ်ခုမှာ အောက်ဖော်ပြပါ ယူဆချက်များကို အသုံးပြုသည့် စာရင်းအင်းဆိုင်ရာစမ်းသပ်မှုဖြစ်သည့် Brown-Forsythe test ကို အသုံးပြုခြင်းဖြစ်သည်။

• H ₀ : လူဦးရေများကြား ကွဲလွဲမှုများသည် တန်းတူဖြစ်သည်။
• H _A : လူဦးရေ ကွာဟချက်က မညီမျှပါဘူး။

စမ်းသပ်မှု၏ p-တန်ဖိုး သည် အချို့သော အရေးပါမှုအဆင့်အောက်တွင် ရှိပါက (ဥပမာ α = 0.05)၊ ထို့နောက် null hypothesis ကို ငြင်းပယ်ပြီး မတူညီသော လူဦးရေများကြားတွင် ကွဲပြားမှုများ မညီမျှကြောင်း ကောက်ချက်ချပါသည်။

ဤသင်ခန်းစာသည် R တွင် Brown-Forsythe စမ်းသပ်မှုပြုလုပ်ပုံအဆင့်ဆင့်ကို ဥပမာပေးထားသည်။

အဆင့် 1: ဒေတာကိုထည့်ပါ။

မတူညီတဲ့ လေ့ကျင့်ခန်း အစီအစဉ်သုံးခုက မတူညီတဲ့ ကိုယ်အလေးချိန်ကို လျော့ကျစေသလားဆိုတာကို ကျွန်ုပ်တို့ သိလိုသည်ဆိုပါစို့။

၎င်းကိုစမ်းသပ်ရန်အတွက် ကျွန်ုပ်တို့သည် လူ 90 ကိုစုဆောင်းပြီး ပရိုဂရမ်တစ်ခုစီကိုအသုံးပြုရန် 30 ကို ကျပန်းသတ်မှတ်ပေးပါသည်။ ထို့နောက် တစ်လအကြာတွင် လူတစ်ဦးစီ၏ ကိုယ်အလေးချိန်ကို တိုင်းတာသည်။

အောက်ဖော်ပြပါ ဒေတာအတွဲတွင် ပရိုဂရမ်တစ်ခုစီတွင် ဆုံးရှုံးသွားသော အလေးချိန်ပမာဏဆိုင်ရာ အချက်အလက်ပါရှိသည်။

 #make this example reproducible
set.seed(0)

#create data frame
data <- data.frame(program = as . factor ( rep (c(" A ", " B ", " C "), each = 30)),
                   weight_loss = c( runif (30, 0, 3),
                                   runif (30, 0, 5),
                                   runif (30, 1, 7)))

#view first six rows of data frame
head(data)

# program weight_loss
#1 A 2.6900916
#2 A 0.7965260
#3 A 1.1163717
#4 A 1.7185601
#5 A 2.7246234
#6 A 0.6050458

အဆင့် 2- ဒေတာကို အကျဉ်းချုပ်ပြီး မြင်ယောင်ကြည့်ပါ။

Brown-Forsythe စမ်းသပ်မှုကို မလုပ်ဆောင်မီ၊ အုပ်စုတစ်ခုစီအတွက် ကိုယ်အလေးချိန်ကျခြင်း၏ ကွဲပြားမှုကို မြင်သာစေရန် အကွက်ကွက်များကို ဖန်တီးနိုင်သည်-

 boxplot(weight_loss ~ program, data = data)

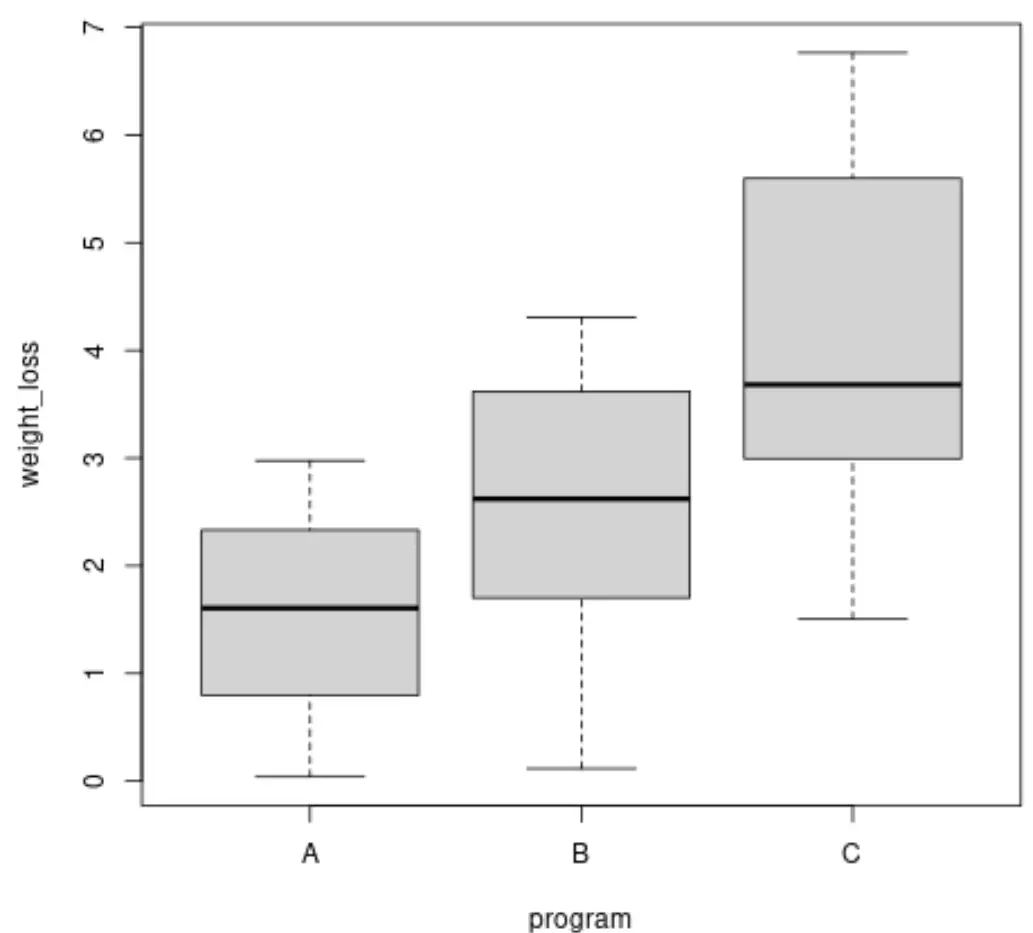
အုပ်စုတစ်ခုစီရှိ ကိုယ်အလေးချိန်ကျခြင်း၏ ကွဲပြားမှုကိုလည်း တွက်ချက်နိုင်သည်။

 #load dplyr package
library (dplyr)

#calculate variance of weight loss by group
data %>%
group_by (program) %>%
  summarize (var=var(weight_loss))

# A tibble: 3 x 2
  program var
     
1 A 0.819
2 B 1.53 
3 C 2.46

အဖွဲ့များကြား ကွဲလွဲမှုများ ကွဲပြားသည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်သော်လည်း ဤကွာခြားချက်များသည် ကိန်းဂဏန်းအရ သိသာထင်ရှားခြင်း ရှိမရှိ ဆုံးဖြတ်ရန်၊ ကျွန်ုပ်တို့သည် Brown-Forsythe စမ်းသပ်မှုကို လုပ်ဆောင်နိုင်ပါသည်။

အဆင့် 3- Brown-Forsythe စမ်းသပ်မှုကို လုပ်ဆောင်ပါ။

R တွင် Brown-Forsythe စမ်းသပ်မှုကို လုပ်ဆောင်ရန်၊ ကျွန်ုပ်တို့သည် onewaytests ပက်ကေ့ခ်ျမှ bf.test() လုပ်ဆောင်ချက်ကို အသုံးပြုနိုင်ပါသည်။

 #load onewaytests package
library (onewaytests)

#perform Brown-Forsythe test
bf.test(weight_loss ~ program, data = data)

  Brown-Forsythe Test (alpha = 0.05) 
-------------------------------------------------- ----------- 
  data: weight_loss and program 

  statistic: 30.83304 
  num df: 2 
  name df: 74.0272 
  p.value: 1.816529e-10 

  Result: Difference is statistically significant. 
-------------------------------------------------- -----------

စစ်ဆေးမှု၏ p-value သည် 0.000 ထက်နည်းပြီး ရလဒ်ကဖော်ပြသည့်အတိုင်း အုပ်စုသုံးစုကြားကွဲလွဲမှုများသည် စာရင်းအင်းအရ သိသာထင်ရှားပါသည်။

နောက်တစ်ဆင့်

Brown-Forsythe စမ်းသပ်မှု၏ null hypothesis ကို သင် မငြင်းပယ်နိုင်ပါက၊ သင်သည် data ပေါ်တွင် one-way ANOVA ကို လုပ်ဆောင်နိုင်သည်။

သို့ရာတွင်၊ သင်သည် null hypothesis ကို ငြင်းပယ်ပါက၊ ကွဲပြားမှုများ၏ တန်းတူညီမျှမှု၏ ယူဆချက်ကို ချိုးဖောက်သည်ဟု ဆိုလိုသည်။ ဤကိစ္စတွင်၊ သင့်တွင် ရွေးချယ်စရာနှစ်ခုရှိသည်။

1. ANOVA တစ်ကြောင်းတည်းလုပ်ပါ။

အကြီးဆုံးကွဲလွဲမှုသည် အသေးငယ်ဆုံးကွဲလွဲမှု 4 ဆထက်မပိုသရွေ့ တစ်လမ်းသွား ANOVA သည် မညီမျှသောကွဲလွဲချက်များနှင့် ခိုင်ခံ့မှုရှိသည် ။

အထက်ဖော်ပြပါ ဥပမာ၏ အဆင့် 2 တွင်၊ အသေးငယ်ဆုံးကွဲလွဲမှုမှာ 0.819 ဖြစ်ပြီး အကြီးဆုံးကွဲလွဲမှုမှာ 2.46 ဖြစ်ကြောင်း တွေ့ရှိရပါသည်။ ထို့ကြောင့် အကြီးဆုံးနှင့် အငယ်ဆုံးကွဲလွဲမှု၏ အချိုးသည် 2.46 / 0.819 = 3.003 ဖြစ်သည်။

ဤတန်ဖိုးသည် 4 ထက်နည်းသောကြောင့်၊ ကျွန်ုပ်တို့သည် one-way ANOVA ကို ရိုးရှင်းစွာလုပ်ဆောင်နိုင်သည်။

2. Kruskal-Wallis စမ်းသပ်မှုပြုလုပ်ပါ။

အငယ်ဆုံးကွဲလွဲချက်နှင့် အကြီးဆုံးကွဲလွဲမှု၏အချိုးသည် 4 ထက်ကြီးပါက၊ ၎င်းအစား Kruskal-Wallis စမ်းသပ်မှုကို လုပ်ဆောင်ရန် ရွေးချယ်နိုင်သည်။ ၎င်းကို တစ်လမ်းမောင်း ANOVA ၏ စံမညီသော တိုင်းတာမှု ညီမျှသည်ဟု ယူဆပါသည်။

R တွင် Kruskal-Wallis စမ်းသပ်မှု၏ အဆင့်ဆင့် ဥပမာကို ဤနေရာတွင် ရှာနိုင်သည်။