Stata တွင် အထက်အောက် ဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်နည်း

Hierarchical regression သည် မတူညီသော linear model အများအပြားကို နှိုင်းယှဉ်ရန် အသုံးပြုနိုင်သော နည်းပညာတစ်ခုဖြစ်သည်။

အခြေခံအယူအဆမှာ ကျွန်ုပ်တို့သည် ပထမဦးစွာ ရှင်းလင်းချက်ပြောင်းနိုင်သောကိန်းရှင်တစ်ခုဖြင့် linear regression model ကို ဖြည့်သွင်းရန်ဖြစ်သည်။ ထို့နောက်၊ ကျွန်ုပ်တို့သည် အပိုရှင်းပြချက်ကိန်းရှင်ကို အသုံးပြု၍ အခြားသော ဆုတ်ယုတ်မှုပုံစံနှင့် ကိုက်ညီပါသည်။ R-squared (ရှင်းပြချက် variable များဖြင့် ရှင်းပြနိုင်သော တုံ့ပြန်မှုကိန်းရှင်တွင် ကွဲလွဲမှုအချိုးအစား) သည် ဒုတိယမော်ဒယ်ရှိ R-squared ထက် သိသိသာသာ မြင့်မားနေပါက၊ ၎င်းသည် ဒုတိယမော်ဒယ်သည် ပိုကောင်းသည်ဟု ဆိုလိုသည်။

ထို့နောက် ကျွန်ုပ်တို့သည် ထပ်လောင်းရှင်းပြထားသော ကိန်းရှင်များနှင့်အတူ ထပ်လောင်းဆုတ်ယုတ်မှုပုံစံများကို အံဝင်ခွင်ကျဖြစ်အောင် ပြန်လုပ်ကာ မော်ဒယ်အသစ်များသည် ယခင်မော်ဒယ်များထက် ပိုမိုကောင်းမွန်လာမှုရှိမရှိ ကြည့်ရှုပါ။

ဤသင်ခန်းစာသည် Stata တွင် အထက်အောက် ဆုတ်ယုတ်မှုလုပ်ဆောင်နည်းကို ဥပမာပေးသည်။

ဥပမာ- Stata ရှိ အထက်အောက် ဆုတ်ယုတ်မှု

Stata တွင် အထက်အောက် ဆုတ်ယုတ်မှုအား မည်သို့လုပ်ဆောင်ရမည်ကို သရုပ်ဖော်ရန် auto ဟုခေါ်သည့် ပါ၀င်သည့်ဒေတာအတွဲကို အသုံးပြုပါမည်။ ပထမဦးစွာ၊ command box တွင် အောက်ပါတို့ကို ရိုက်ထည့်ခြင်းဖြင့် dataset ကို တင်ပါ-

အလိုအလျောက်စနစ်အသုံးပြုခြင်း။

အောက်ပါ command ကို အသုံးပြု၍ ဒေတာ၏ အမြန်အကျဉ်းချုပ်ကို ကျွန်ုပ်တို့ ရနိုင်သည်-

အကျဉ်းချုပ်ရန်

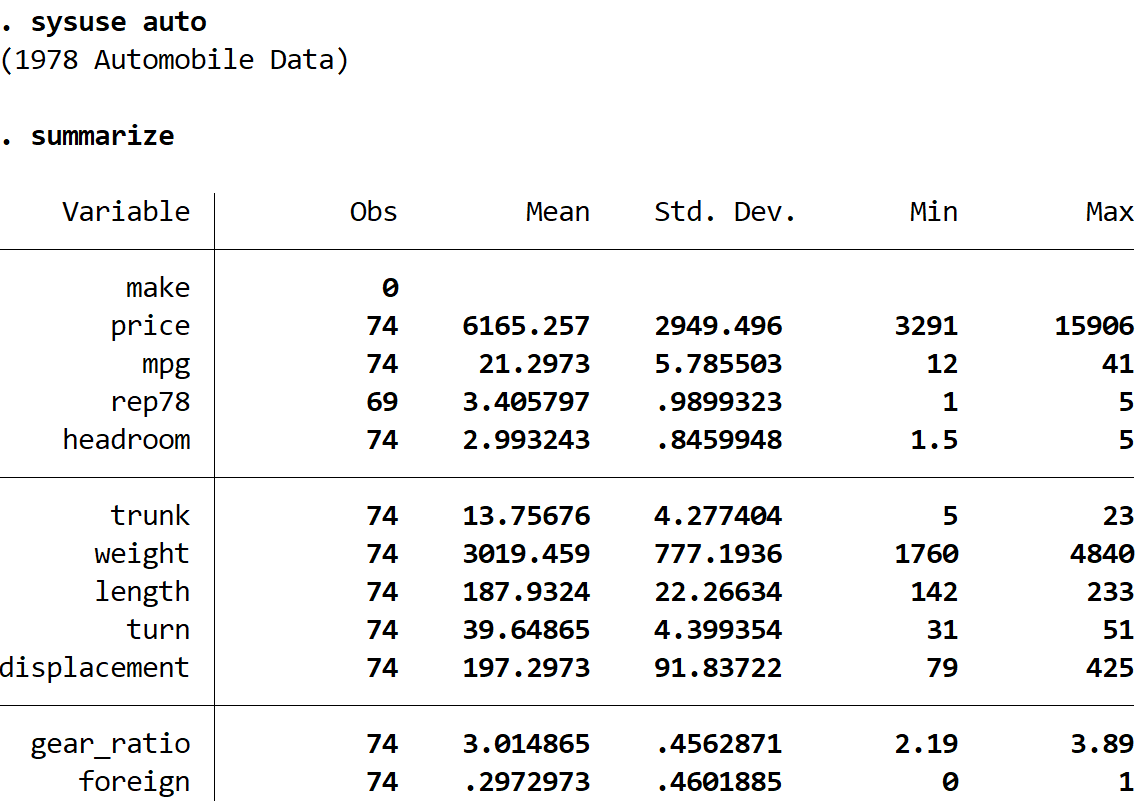
ဒေတာအတွဲတွင် စုစုပေါင်းကား ၇၄ စီးအတွက် မတူညီသော ကိန်းရှင် ၁၂ ခုတွင် အချက်အလက်များ ပါဝင်သည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။

ကျွန်ုပ်တို့သည် အောက်ဖော်ပြပါ မျဉ်းဖြောင့်ဆုတ်ယုတ်မှုပုံစံသုံးမျိုးနှင့် အံဝင်ခွင်ကျဖြစ်ပြီး နောက်ဆက်တွဲမော်ဒယ်တစ်ခုစီသည် ယခင်မော်ဒယ်ထက် သိသာထင်ရှားသောတိုးတက်မှုကို ပံ့ပိုးပေးသည်ရှိမရှိကို ကြည့်ရှုရန် အထက်အောက်ဆုတ်ယုတ်မှုကို အသုံးပြုပါမည်။

မော်ဒယ် 1- စျေးနှုန်း = ကြားဖြတ် + စိုင်းစိုင်းခမ်းလှိုင်

မော်ဒယ် 2- စျေးနှုန်း = ကြားဖြတ် + စိုင်းစိုင်းခမ်းလှိုင် + အလေးချိန်

မော်ဒယ် 3- စျေးနှုန်း = ကြားဖြတ် + စိုင်းစိုင်းခမ်းလှိုင် + အလေးချိန် + ဂီယာအချိုး

Stata ရှိ အထက်အောက် ဆုတ်ယုတ်မှုကို လုပ်ဆောင်ရန်အတွက်၊ ကျွန်ုပ်တို့သည် ဦးစွာ Hireg ပက်ကေ့ခ်ျကို ထည့်သွင်းရန် လိုအပ်ပါသည်။ ဒီလိုလုပ်ဖို့၊ Command box မှာ အောက်ပါအတိုင်း ရိုက်ထည့်ပါ။

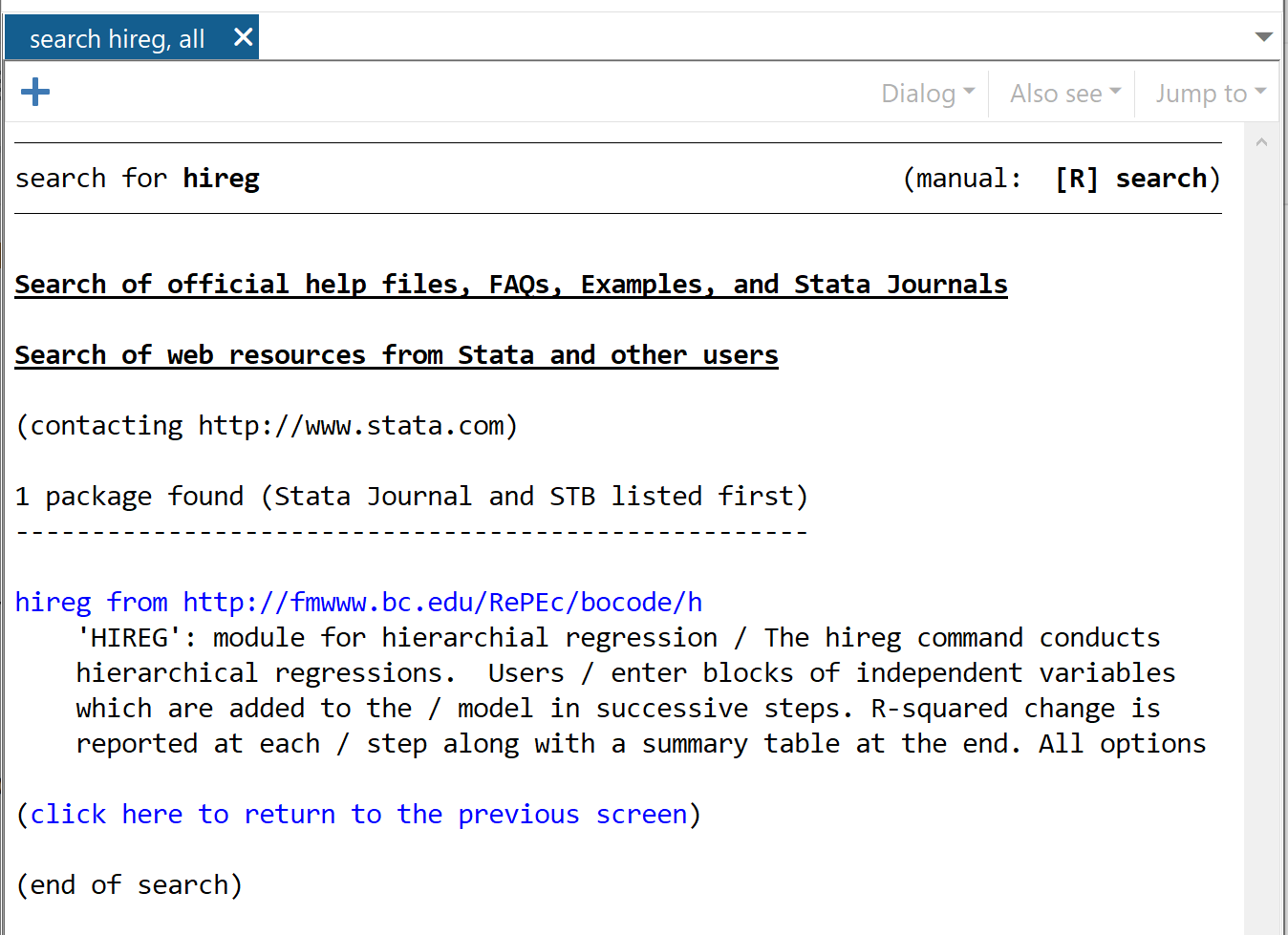
Hireg ကိုရှာပါ။

ပေါ်လာသောဝင်းဒိုးတွင်၊ https://fmwww.bc.edu/RePEc/bocode/h မှ Hireg ကိုနှိပ်ပါ။

လာမည့်ဝင်းဒိုးတွင်၊ ထည့်သွင်းရန် ဤနေရာကို နှိပ်ပါ ဟူသော လင့်ခ်ကို နှိပ်ပါ။

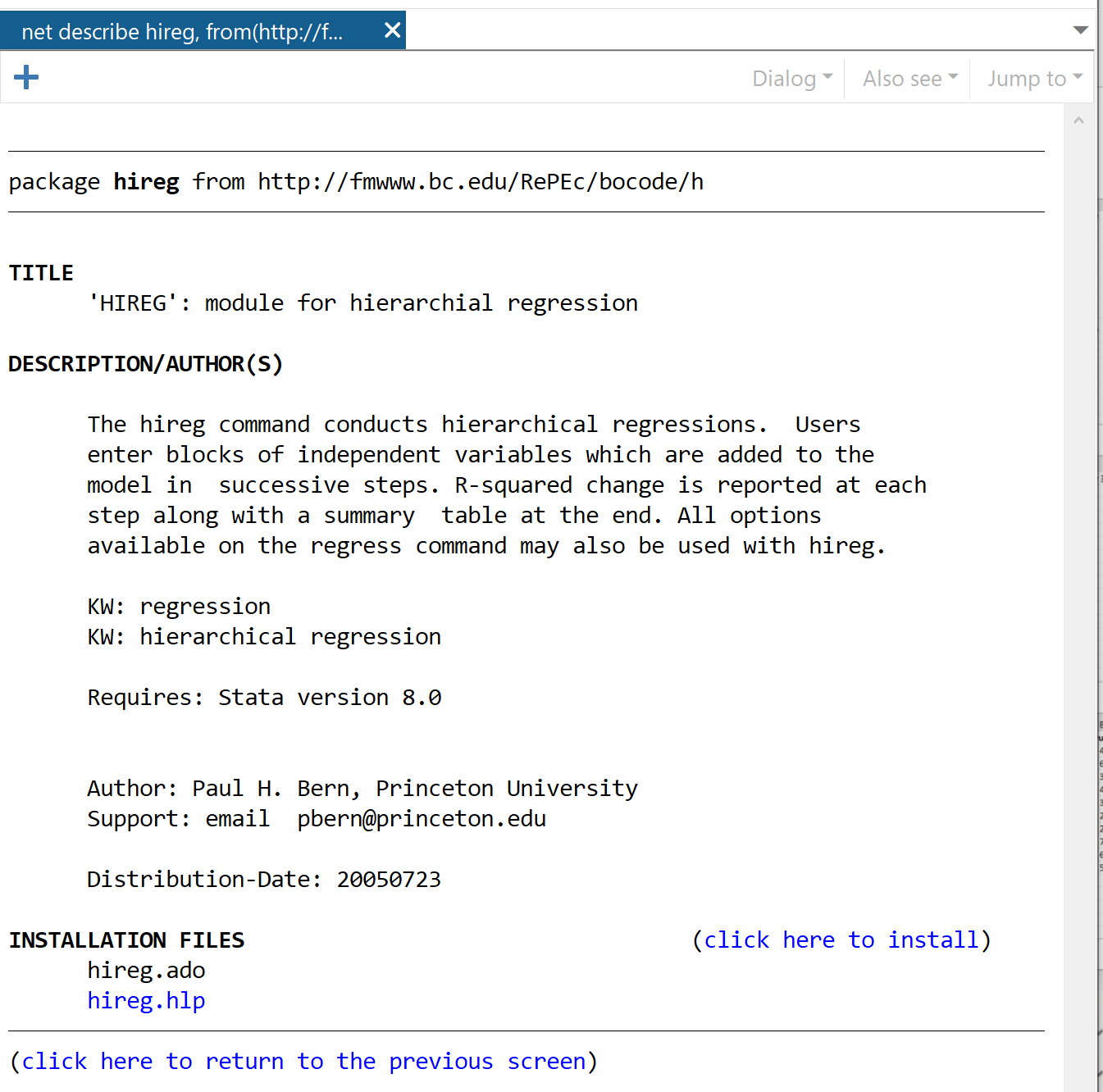
အထုပ်သည် စက္ကန့်ပိုင်းအတွင်း ထည့်သွင်းပါမည်။ ထို့နောက် hierarchical regression လုပ်ဆောင်ရန်၊ ကျွန်ုပ်တို့သည် အောက်ပါ command ကို အသုံးပြုပါမည်-

အငှားစျေးနှုန်း (စိုင်းစိုင်းခမ်းလှိုင်) (အလေးချိန်) (ဂီယာ_အချိုး)

ဒါက Stata ခိုင်းစေတဲ့အရာပါ။

• မော်ဒယ်တစ်ခုစီရှိ တုံ့ပြန်မှုကိန်းရှင်အဖြစ် စျေးနှုန်းကို အသုံးပြု၍ အထက်အောက် ဆုတ်ယုတ်မှုကို လုပ်ဆောင်ပါ။
• ပထမမော်ဒယ်အတွက်၊ ရှင်းပြချက်ပြောင်းလဲနိုင်သောအဖြစ် mpg ကို သုံးပါ။
• ဒုတိယမော်ဒယ်အတွက်၊ အလေးချိန်ကို ထပ်လောင်းရှင်းပြချက်တစ်ခုအဖြစ် ပေါင်းထည့်ပါ။
• တတိယမော်ဒယ်အတွက်၊ နောက်ထပ်ရှင်းပြချက်တစ်ခုအဖြစ် gear_ratio ကို ထည့်ပါ။

ဤသည်မှာ ပထမမော်ဒယ်၏ ရလဒ်ဖြစ်သည်။

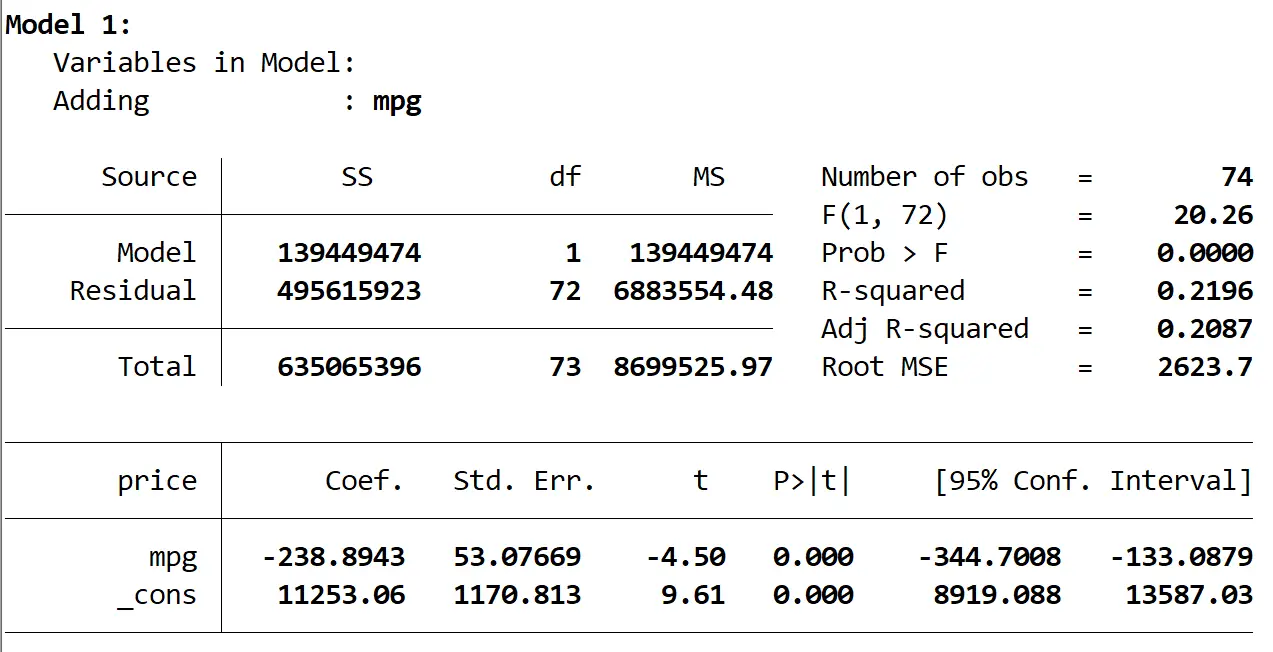
မော်ဒယ်၏ R-squared သည် 0.2196 ဖြစ်ပြီး မော်ဒယ်၏ စုစုပေါင်း p-value (Prob > F) သည် 0.0000 ဖြစ်ပြီး ကိန်းဂဏန်းအရ သိသာထင်ရှားသော α = 0.05 ဖြစ်သည်။

ထို့နောက်၊ ဒုတိယမော်ဒယ်၏ရလဒ်ကိုကျွန်ုပ်တို့မြင်ရသည်-

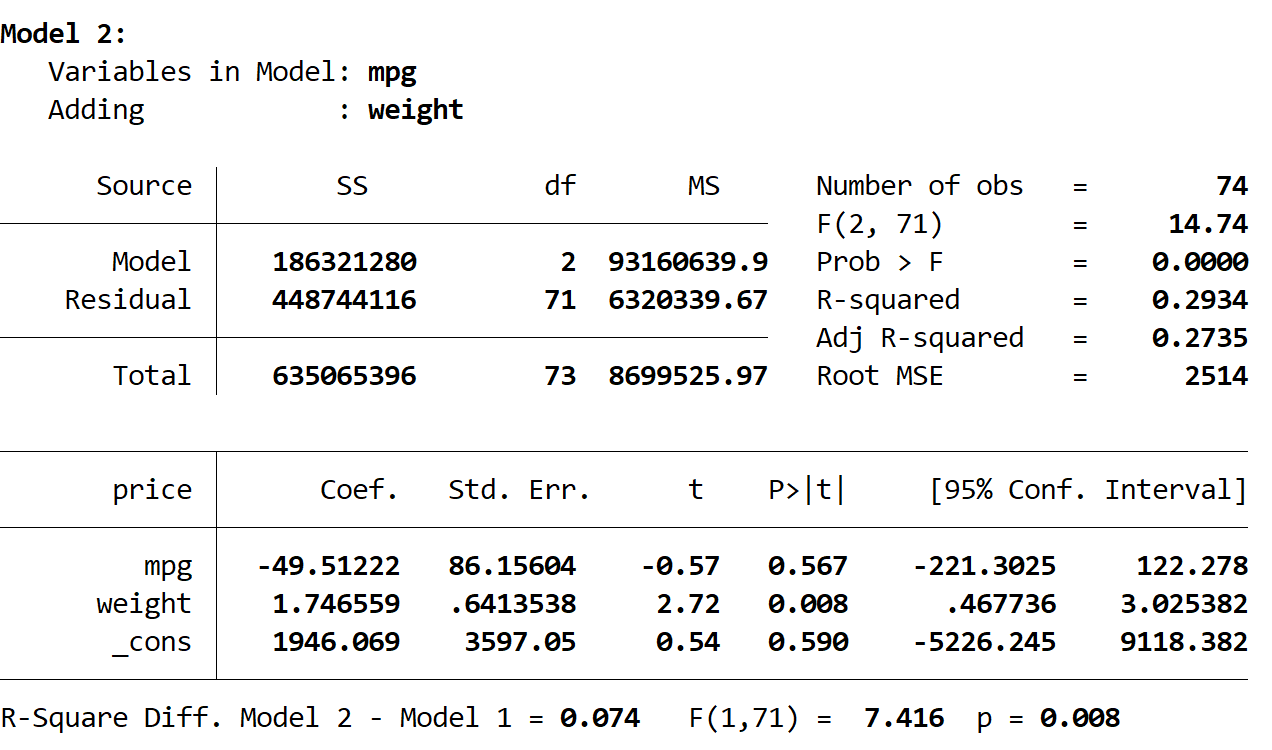
ဤမော်ဒယ်၏ R စတုရန်းသည် 0.2934 ဖြစ်ပြီး၊ ၎င်းသည် ပထမမော်ဒယ်ထက် ပိုကြီးသည်။ ဤကွာခြားချက်သည် ကိန်းဂဏန်းအရ သိသာထင်ရှားခြင်းရှိ၊ မရှိ ဆုံးဖြတ်ရန်၊ Stata သည် ရလဒ်၏အောက်ခြေရှိ အောက်ပါနံပါတ်များကိုပေးသည့် F-test ကို လုပ်ဆောင်ခဲ့သည်-

• R နှစ်ထပ်ကိန်း မော်ဒယ်နှစ်ခုကြား ခြားနားချက် = 0.074
• ကွာခြားချက်အတွက် F ကိန်းဂဏန်း = 7.416
• F ကိန်းဂဏန်း = 0.008 ၏ သက်ဆိုင်ရာ p-တန်ဖိုး

p-value သည် 0.05 ထက်နည်းသောကြောင့်၊ ပထမမော်ဒယ်နှင့် နှိုင်းယှဉ်ပါက ဒုတိယမော်ဒယ်တွင် ကိန်းဂဏန်းသိသိသာသာ တိုးတက်မှုရှိကြောင်း ကျွန်ုပ်တို့ ကောက်ချက်ချပါသည်။

နောက်ဆုံးတွင်၊ တတိယပုံစံ၏ရလဒ်ကိုကျွန်ုပ်တို့မြင်နိုင်သည်:

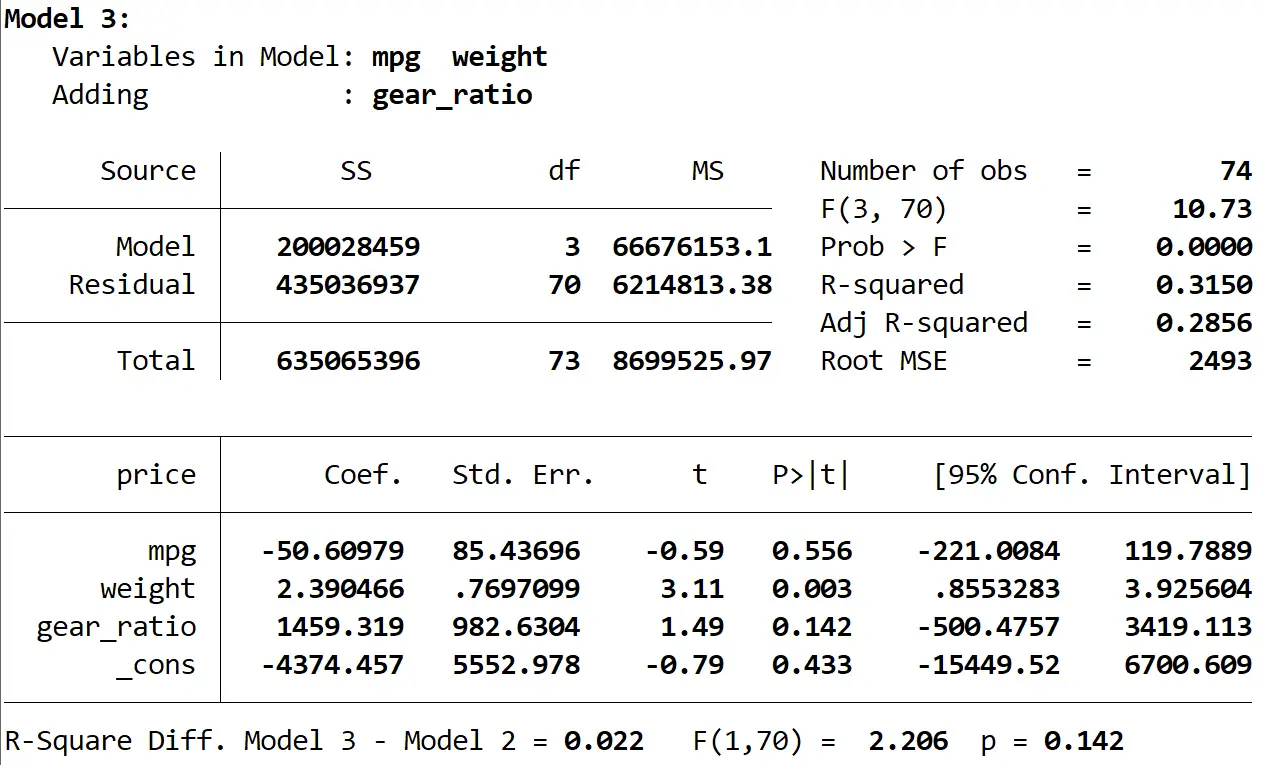
ဤမော်ဒယ်၏ R စတုရန်းသည် 0.3150 ဖြစ်ပြီး၊ ၎င်းသည် ဒုတိယမော်ဒယ်ထက် ပိုကြီးသည်။ ဤကွာခြားချက်သည် ကိန်းဂဏန်းအရ သိသာထင်ရှားခြင်းရှိ၊ မရှိ ဆုံးဖြတ်ရန်၊ Stata သည် ရလဒ်၏အောက်ခြေရှိ အောက်ပါနံပါတ်များကိုပေးသည့် F-test ကို လုပ်ဆောင်ခဲ့သည်-

• R နှစ်ထပ်ကိန်း မော်ဒယ်နှစ်ခုကြား ခြားနားချက် = 0.022
• ကွာခြားချက်အတွက် F ကိန်းဂဏန်း = 2.206
• သက်ဆိုင်သော p-တန်ဖိုး F ကိန်းဂဏန်း = 0.142

p-value သည် 0.05 ထက်မနည်းသောကြောင့်၊ တတိယမော်ဒယ်သည် ဒုတိယမော်ဒယ်ထက် ပိုမိုကောင်းမွန်လာသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထားမရှိပါ။

ရလဒ်၏အဆုံးတွင်၊ Stata သည် ရလဒ်များ၏ အကျဉ်းချုပ်ကို ပံ့ပိုးပေးသည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်-

ဤဥပမာတွင်၊ Model 2 သည် Model 1 ထက် သိသာထင်ရှားသော တိုးတက်မှုကို ပေးစွမ်းနိုင်သည်ဟု ကျွန်ုပ်တို့ ကောက်ချက်ချနိုင်သည်၊ သို့သော် Model 3 သည် Model 2 ထက် သိသာထင်ရှားသော တိုးတက်မှုကို ပေးစွမ်းနိုင်ခြင်း မရှိပေ။