အနုတ်လက္ခဏာနှစ်ခုခွဲဝေမှု

အားဖြင့် Benjamin Anderson ဩဂုတ် 3, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် အနုတ်လက္ခဏာ binomial ဖြန့်ဝေမှုမှာ အဘယ်အရာနှင့် ၎င်းကိုအသုံးပြုကြောင်း ရှင်းပြထားသည်။ အနုတ်လက္ခဏာ binomial ဖြန့်ဖြူးမှုအတွက် ဖော်မြူလာ၊ ခိုင်မာသော ဥပမာတစ်ခုနှင့် ဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုအမျိုးအစား၏ ဂုဏ်သတ္တိများကို သင်တွေ့လိမ့်မည်။ နောက်ဆုံးတွင်၊ သင်သည် အွန်လိုင်းဂဏန်းတွက်စက်ဖြင့် အနုတ်လက္ခဏာ binomial ဖြန့်ဖြူးမှုဖြစ်နိုင်ခြေကို တွက်ချက်နိုင်မည်ဖြစ်သည်။

အနုတ်လက္ခဏာ binomial ဖြန့်ဖြူးမှုကား အဘယ်နည်း။

အနုတ်လက္ခဏာ binomial ဖြန့်ဝေမှုသည် ပေးထားသော အပြုသဘောဆောင်သောရလဒ်များရရှိရန် လိုအပ်သော Bernoulli စမ်းသပ်မှုအရေအတွက်ကို ဖော်ပြသည့် ဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။

ထို့ကြောင့်၊ အနုတ်လက္ခဏာ binomial ဖြန့်ဝေမှုတွင် ဝိသေသဘောင်နှစ်ခုရှိသည်- r သည် လိုချင်သော အောင်မြင်သောရလဒ်များ၏ အရေအတွက်ဖြစ်ပြီး p သည် Bernoulli စမ်းသပ်မှုတစ်ခုစီအတွက် အောင်မြင်နိုင်ခြေဖြစ်နိုင်ခြေဖြစ်သည်။

$X\sim \text{BN}(r,p)$

Bernoulli စမ်းသပ်မှုသည် “ အောင်မြင်မှု” နှင့် “ ကျရှုံးခြင်း” ဖြစ်နိုင်သောရလဒ်နှစ်ခုရှိသည်သောစမ်းသပ်မှုတစ်ခုဖြစ်ကြောင်းသတိရပါ။ ထို့ကြောင့် “ အောင်မြင်မှု” ၏ဖြစ်နိုင်ခြေသည် p ဖြစ်ပါက “ ကျရှုံးခြင်း” ဖြစ်နိုင်ခြေမှာ q=1-p ဖြစ်သည်။

ထို့ကြောင့်၊ အနုတ်လက္ခဏာ binomial ဖြန့်ဝေမှုသည် အပြုသဘောဆောင်သော ရလဒ်များ ရရှိရန် လိုအပ်သလို Bernoulli စမ်းသပ်မှုများစွာကို လုပ်ဆောင်သည့် လုပ်ငန်းစဉ်ကို သတ်မှတ်သည်။ ထို့အပြင်၊ ဤ Bernoulli စမ်းသပ်မှုများအားလုံးသည် သီးခြားလွတ်လပ်ပြီး အောင်မြင်မှု ၏ အဆက်မပြတ်ဖြစ်နိုင်ခြေရှိသည်။

ဥပမာအားဖြင့်၊ အနုတ်လက္ခဏာ binomial ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်သော ကျပန်း variable သည် နံပါတ် 6 ကို သုံးကြိမ်လှိမ့်သည်အထိ လှိမ့်ရမည့် အကြိမ်အရေအတွက်ဖြစ်သည်။

အနုတ်လက္ခဏာ binomial ဖြန့်ဝေမှုနှင့် binomial ဖြန့်ဝေမှုကြား ခြားနားချက်မှာ အနုတ်ဘွယ်ဖြန့်ဖြူးမှုသည် အချို့သော အောင်မြင်သောရလဒ်များရရှိရန် လိုအပ်သည့်အကြိမ်အရေအတွက်ကို ရေတွက်ပြီး Bernoulli စမ်းသပ်မှုစီးရီးတစ်ခုတွင် အောင်မြင်သောဖြစ်ရပ်အရေအတွက်ကို ရေတွက်နေချိန်တွင်၊

➤ ကြည့်ပါ- binomial distribution ကဘာလဲ။

အနုတ်လက္ခဏာ binomial ဖြန့်ဖြူးမှုဖော်မြူလာ

ကန့်သတ်ဘောင်များကို r, p, x ဖြင့် ပေးထားသည့် အနုတ်လက္ခဏာ binomial ဖြန့်ဖြူးခြင်း၏ ဖြစ်နိုင်ခြေကို xr တွင် ( 1 -p) ^xr ဖြင့် p ^r ဖြင့် ပေါင်းစပ်ထားသော နံပါတ်ကို မြှောက်ခြင်းဖြင့် တွက်ချက်သည်။

ထို့ကြောင့်၊ အနုတ်လက္ခဏာ binomial ဖြန့်ဖြူးမှုဖြစ်နိုင်ခြေကို တွက်ချက်ရန်အတွက် ဖော်မြူလာ မှာ-

အနုတ်လက္ခဏာ binomial ဖြန့်ဖြူးမှုဖော်မြူလာ

👉 အနုတ်လက္ခဏာ binomial ဖြန့်ဖြူးမှုနောက်ဆက်တွဲဖြစ်သော variable ၏ဖြစ်နိုင်ခြေကိုတွက်ချက်ရန် အောက်ပါဂဏန်းတွက်စက်ကို သင်အသုံးပြုနိုင်ပါသည်။

အနုတ်လက္ခဏာ binomial ဖြန့်ဖြူးမှု၏ဖြေရှင်းချက်လေ့ကျင့်ခန်း

အကြွေစေ့တစ်ပြားကို ရှစ်ကြိမ်လောက်ပစ်ရင် အဋ္ဌမမြောက်အကြိမ်မှာ စတုတ္ထအကြိမ် ခေါင်းပေါ်တက်လာနိုင်ခြေ ဘယ်လောက်ရှိလဲ။

ဦးစွာ၊ အကြွေစေ့ပစ်သောအခါ ဦးခေါင်းရနိုင်ခြေကို တွက်ချက်ရန် လိုအပ်သည်။ ဤကိစ္စတွင်၊ ကျွန်ုပ်တို့တွင် ဖြစ်နိုင်ချေရှိသော ရလဒ်နှစ်ခု (ခေါင်းနှင့် အမြီးများ) မှ အပြုသဘောဆောင်သော ရလဒ် (ဦးခေါင်း) တစ်ခုသာ ရှိသည်၊ ထို့ကြောင့် အောင်မြင်မှု၏ ဖြစ်နိုင်ခြေမှာ-

$p=\cfrac{1}{2}=0,5$

ထို့ကြောင့်၊ ဤပြဿနာရှိ ကျပန်းပြောင်းလဲနိုင်သောကိန်းရှင်သည် r=4 နှင့် p=0.5 ရှိသော အနုတ်လက္ခဏာ binomial ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်သည်။ ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် လေ့ကျင့်ခန်းလုပ်ခိုင်းသည့် ဖြစ်နိုင်ခြေကို တွက်ချက်ရန် အနုတ်လက္ခဏာ binomial ဖြန့်ဝေမှုဖော်မြူလာကို အသုံးပြုပါသည်။

$\begin{aligned}P[X=x]&=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r\\[2ex]\displaystyle P[X=8]&=\begin{pmatrix}8-1\\ 8-4\end{pmatrix}\cdot (1-0,5)^{8-4}\cdot 0,5^4\\[2ex] P[X=8]&=0,1367\end{aligned}$

အနှုတ် binomial ဖြန့်ဖြူးခြင်း၏လက္ခဏာများ

အောက်ဖော်ပြပါများသည် အနုတ်လက္ခဏာ binomial ဖြန့်ဖြူးခြင်း၏ အရေးကြီးဆုံးလက္ခဏာများဖြစ်သည်။

အနုတ်လက္ခဏာ binomial ဖြန့်ဖြူးမှုကို လက္ခဏာရပ်နှစ်ခုဖြင့် သတ်မှတ်သည်- r သည် လိုချင်သော အောင်မြင်သောရလဒ်များ၏ အရေအတွက်ဖြစ်ပြီး p သည် Bernoulli စမ်းသပ်မှုတစ်ခုစီအတွက် အောင်မြင်မှုဖြစ်နိုင်ခြေဖြစ်သည်။

 *** QuickLaTeX cannot compile formula:
\begin{array}{c}r\in \mathbb{Z}^+ \\[2ex] 0 <ul><li> The mean of the negative binomial distribution is equal to <em>r</em> multiplied by <em>(1-p)</em> and divided by <em>p</em> . Thus the formula which makes it possible to calculate the mean of a negative binomial distribution is the following: </li></ul>[latex]E[X]=\cfrac{r\cdot (1-p)}{p}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{c}
Please use \mathaccent for accents in math mode.
leading text: ...The mean of the binomial distribution born
Please use \mathaccent for accents in math mode.
leading text: ... the negative binomial distribution is
Please use \mathaccent for accents in math mode.
leading text: ...negative binomial distribution is equal to
Please use \mathaccent for accents in math mode.
leading text: ...gative is equal to <em>r</em> multiplied
Please use \mathaccent for accents in math mode.
leading text: ...m> multiplied by <em>(1-p)</em> and divided
Please use \mathaccent for accents in math mode.
leading text: ...the mean of a binomial distribution born
\begin{array} on input line 8 ended by \end{document}.

အနုတ်နှစ်လုံးခွဲဝေမှု၏ကွဲလွဲမှုသည် r နှင့် ညီမျှသည် (1-p) ဖြင့် p ² ဖြင့် မြှောက်သည်။

$Var(X)=\cfrac{r\cdot (1-p)}{p^2}$

ကန့်သတ်ဘောင် r သည် 1 ထက် ကြီးပါက၊ အနုတ်လက္ခဏာ binomial ဖြန့်ဝေမှုပုံစံကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်နိုင်သည်-

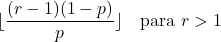
$\displaystyle \lfloor \frac{(r-1)(1-p)}{p}\rfloor\quad \text{para }r>1″ title=” Rendered by QuickLaTeX.com” height=” 42″ width=” 221″ style=” vertical-align: -16px;” ></p> </p> <ul> <li> အနုတ်လက္ခဏာ binomial ဖြန့်ဖြူးမှု၏ဖြစ်နိုင်ခြေကိုဆုံးဖြတ်ရန်ဖြစ်နိုင်ချေရှိသောဒြပ်ထုလုပ်ဆောင်မှုမှာအောက်ပါအတိုင်းဖြစ်သည်။</li> </ul> <p class=$ $P[X=x]=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r$

အနုတ်လက္ခဏာ binomial ဖြန့်ဖြူးမှု၏ skewness coefficient ကို အောက်ပါအသုံးအနှုန်းဖြင့် တွက်ချက်သည်-

$\displaystyle A=\frac{2-p}{\sqrt{r\,(1-p)}}$

အနုတ်လက္ခဏာ binomial ဖြန့်ဖြူးမှု၏ kurtosis ကို အောက်ပါဖော်မြူလာဖြင့် တွေ့ရှိနိုင်သည်။

$\displaystyle C=\frac{6}{r} + \frac{p^2}{r\,(1-p)}$

ကန့်သတ်ဘောင် r သည် 1 နှင့် ညီမျှပါက၊ ကျွန်ုပ်တို့တွင် ဂျီဩမေတြီ ဖြန့်ဝေမှု ကိစ္စတစ်ခုရှိသည်။

$r=1 \quad\color{orange}\bm{\longrightarrow}\color{black}\quad X\sim \text{Geometrica}(p)$

Negative Binomial Distribution Calculator

ဖြစ်နိုင်ခြေကိုတွက်ချက်ရန် အောက်ပါဂဏန်းပေါင်းစက်ထဲသို့ ကန့်သတ်ဘောင်များ r, p, x ၏တန်ဖိုးများကို ထည့်ပါ။ ဥပမာအားဖြင့် 0.50 ကို ဒဿမ ခြားနားချက်အဖြစ် အစက်ကို အသုံးပြု၍ နံပါတ်များ ထည့်ရပါမည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။