အမည်မျိုးစုံ ဖြန့်ဖြူးခြင်း။

အားဖြင့် Benjamin Anderson ဩဂုတ် 4, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤဆောင်းပါးသည် စာရင်းဇယားများတွင် အမည်မျိုးစုံ ဖြန့်ဖြူးခြင်းအကြောင်း ရှင်းပြထားသည်။ ထို့ကြောင့်၊ များစွာသောအမည်ခွဲဝေမှု၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်၊ ၎င်း၏ဖော်မြူလာက ဘာလဲ၊ ဖြေရှင်းထားသော လေ့ကျင့်ခန်းနှင့် ဤဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုအမျိုးအစား၏ ဂုဏ်သတ္တိများကား အဘယ်နည်း။ ထို့အပြင်၊ သင်သည် အွန်လိုင်းဂဏန်းတွက်စက်ဖြင့် အမည်မျိုးစုံဖြန့်ဖြူးခြင်း၏ ဖြစ်နိုင်ခြေကို တွက်ချက်နိုင်မည်ဖြစ်သည်။

အမည်မျိုးစုံ ဖြန့်ဖြူးခြင်းဆိုသည်မှာ အဘယ်နည်း။

Multinomial distribution (သို့မဟုတ် multinomial distribution ) သည် စမ်းသပ်မှုများစွာပြီးနောက် အကြိမ်ပေါင်းများစွာ ဖြစ်ပေါ်လာသည့် အပြန်အလှန်သီးသန့်ဖြစ်ရပ်များ၏ ဖြစ်နိုင်ခြေကို ဖော်ပြသည့် ဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။

ဆိုလိုသည်မှာ၊ ကျပန်းစမ်းသပ်မှုတစ်ခုသည် သီးသန့်ဖြစ်ရပ်သုံးခု သို့မဟုတ် ထို့ထက်ပို၍ ဖြစ်ပေါ်လာနိုင်ပြီး ဖြစ်ရပ်တစ်ခုစီ၏ဖြစ်နိုင်ခြေကို သီးခြားစီဖြစ်နိုင်ချေကို သိရှိပါက၊ စမ်းသပ်မှုများစွာကို လုပ်ဆောင်သည့်အခါ ဖြစ်နိုင်ခြေအချို့ကို တွက်ချက်ရန်အတွက် ကိန်းဂဏန်းပေါင်းများစွာ ဖြန့်ဝေခြင်းကို အသုံးပြုပါသည်။ အချိန်တိုင်း

ထို့ကြောင့် multinomial distribution သည် binomial distribution ၏ ယေဘူယျ အဓိပ္ပါယ်ဖြစ်ပါသည်။

Multinomial distribution ဖော်မြူလာ

ကိန်းဂဏန်းမျိုးစုံ ဖြန့်ဖြူးမှုဖြစ်နိုင်ခြေကို တွက်ချက်ရန်၊ ဒေတာစုစုပေါင်း၏ ကိန်းဂဏန်းနှင့် ဖြစ်ရပ်တစ်ခုစီ၏ ဖြစ်ပွားမှုအရေအတွက်၏ factorials အကြား quotient ကို ဦးစွာဆုံးဖြတ်ရမည်ဖြစ်ပြီး ရလဒ်သည် ပွဲတစ်ခုစီ၏ဖြစ်နိုင်ခြေ၏ ရလဒ်ဖြင့် မြှောက်ထားသည်။ အဖြစ်အပျက် အရေအတွက်ကို ယူဆောင်လာသည်။

တစ်နည်းဆိုရသော် Multinomial distribution အတွက် ဖော်မြူလာ မှာ အောက်ပါအတိုင်းဖြစ်သည်။

ရွှေ-

$P$

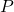
တွက်ချက်ထားသော multinomial distribution ၏ ဖြစ်နိုင်ခြေဖြစ်သည်။
$n$

စစ်ဆေးမှု စုစုပေါင်း အရေအတွက် ဖြစ်ပါသည်။
$x_i$

အဖြစ်အပျက်ဖြစ်ပွားသည့်အကြိမ်အရေအတွက်ဖြစ်သည်။

$i$

.
$p_i$

ဖြစ်ပျက်ခြင်း၏ ဖြစ်နိုင်ခြေသည် အဖြစ်အပျက်ဖြစ်သည်။

$i$

.

👉 Multinomial distribution ၏နောက်ဆက်တွဲဖြစ်သော variable တစ်ခု၏ဖြစ်နိုင်ခြေကိုတွက်ချက်ရန် အောက်ပါ calculator ကို သင်အသုံးပြုနိုင်ပါသည်။

Multinomial Distribution ဥပမာ

များပြားလှသော ဖြန့်ဖြူးခြင်း၏ သဘောတရားကို နားလည်သဘောပေါက်ရန် အပြီးသတ်ရန်၊ အောက်တွင် သင်သည် အမည်မျိုးစုံ ဖြန့်ဖြူးမှုဖြစ်နိုင်ခြေကို တွက်ချက်ခြင်း၏ ဥပမာတစ်ခုကို ဖြေရှင်းထားသည်။

စတိုးဆိုင်တစ်ခုသည် မတူညီသော ထုတ်ကုန်သုံးမျိုး ရောင်းချသည်။ ဖောက်သည်တစ်ဦး ဝယ်ယူသည့်အခါ၊ ၎င်းသည် ထုတ်ကုန် A၊ ထုတ်ကုန် B သို့မဟုတ် ထုတ်ကုန် C ဖြစ်နိုင်သည့် ဖြစ်နိုင်ခြေမှာ 30%, 15% နှင့် 55% အသီးသီးဖြစ်သည်။ စတိုးဆိုင် 8 ယူနစ်ရောင်းချသောအခါဖြစ်နိုင်ခြေကိုရှာပါ 2 ထုတ်ကုန် A ၏ 1 နှင့်ထုတ်ကုန် C ၏ 5 ။

သတ်မှတ်ထားသော ပြဿနာကို အမည်မျိုးစုံ ဖြန့်ဖြူးမှုဖြင့် အုပ်ချုပ်သည်၊ ထို့ကြောင့် ဤဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှုအမျိုးအစားအတွက် ဖော်မြူလာကို အသုံးပြုရန် လိုအပ်သည်-

$P=\cfrac{n!}{x_1!\cdot x_2!\cdot x_3!}\cdot p_1^{x_1}\cdot p_2^{x_2}\cdot p_3^{x_3}$

ထို့ကြောင့် ကျွန်ုပ်တို့သည် ပြဿနာမှဒေတာကို ဖော်မြူလာအဖြစ် အစားထိုးပြီး ဖြစ်နိုင်ခြေတွက်ချက်မှုကို လုပ်ဆောင်သည်-

$P=\cfrac{8!}{2!\cdot 1!\cdot 5!}\cdot 0,30^{2}\cdot 0,15^{1}\cdot 0,55^{5}=0,114$

ထို့ကြောင့် ပြဿနာထုတ်ပြန်ချက်တွင် ဖြစ်ပေါ်လာမည့် ဖြစ်နိုင်ခြေမှာ 11.4% ဖြစ်သည်။

Multinomial Distribution Calculator

ပထမအကွက်တွင် ဖြစ်ရပ်တစ်ခုစီ၏ ဖြစ်ပျက်မှုအရေအတွက်ကို ရေးပြီး ဒုတိယအကွက်တွင် ဖြစ်ရပ်တစ်ခုစီ၏ ဖြစ်နိုင်ခြေကို တူညီသောအစီအစဥ်ဖြင့် ရေးပါ။ ထို့နောက် နောက်ဆုံးနေရာလွတ်တွင် ပြုလုပ်ခဲ့သော စုစုပေါင်းကြိုးစားမှုအရေအတွက်ကို ထည့်ပါ။

ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

အမည်မျိုးစုံ ဖြန့်ဖြူးခြင်း၏ ဂုဏ်သတ္တိများ

Multinomial distribution တွင် အောက်ပါလက္ခဏာများ ရှိပါသည်။

အမည်မျိုးစုံ ဖြန့်ဖြူးမှုတွင်၊ n အစမ်းသုံးမှုများ လုပ်ဆောင်သောအခါတွင် ဖြစ်ပေါ် မည့် အကြိမ်အရေအတွက်၏ မျှော်မှန်းတန်ဖိုးသည် ဖြစ်ရပ်ဖြစ်ပွားနိုင်ခြေဖြင့် မြှောက်ထားသော စမ်းသပ်မှု စုစုပေါင်းအရေအတွက်နှင့် ညီမျှသည်။

$E[x_i]=n\cdot p_i$

အမည်မျိုးစုံ ဖြန့်ဖြူးမှုတွင်၊ ဖြစ်ရပ် i အတွက် ကွဲလွဲမှုကို အောက်ပါအသုံးအနှုန်းဖြင့် တွက်ချက်သည်-

$Var(x_i)=n\cdot p_i\cdot (1-p_i)$

အလားတူ၊ ဖြစ်ရပ်နှစ်ခုကြားရှိ ကွဲလွဲမှုသည် -1 ဖြင့်မြှောက်ထားသော ဖြစ်ရပ်တစ်ခုစီ၏ဖြစ်နိုင်ခြေဖြင့် မြှောက်ထားသော စုစုပေါင်းစမ်းသပ်မှုအရေအတွက်၏ ရလဒ်နှင့် ညီမျှသည်-

$Cov(x_i,x_j)=-n\cdot p_i\cdot p_j\qquad i\neq j$

Multinomial distribution အတွက် function ထုတ်ပေးသည့်အခိုက်မှာ-

$\displaystyle \left(\sum_{i=1}^k p_ie^{t_i}\right) ^n$

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။