အမျိုးအစားခွဲဝေမှုဆိုသည်မှာ အဘယ်နည်း။

အမျိုးအစားခွဲဝေမှု တစ်ခုသည် အမျိုးအစားတစ်ခုစီ၏ဖြစ်နိုင်ခြေနှင့်ဆက်စပ်နေသည့် K အမျိုးအစားတစ်ခု၏တန်ဖိုးကို ကျပန်းကိန်းရှင် တစ်ခုမှယူဆောင်သည့်ဖြစ်နိုင်ခြေကို ဖော်ပြသည့် သီးခြားဖြစ်နိုင်ခြေဖြန့်ဝေမှုတစ်ခုဖြစ်သည်။

ဖြန့်ဖြူးမှုအား အမျိုးအစားခွဲဝေမှုအဖြစ် ခွဲခြားသတ်မှတ်ရန်အတွက်၊ ၎င်းသည် အောက်ပါစံနှုန်းများနှင့် ကိုက်ညီရမည်-

• အမျိုးအစားများသည် သီးခြားဖြစ်သည်။
• ဖြစ်နိုင်ချေ အမျိုးအစား နှစ်ခု သို့မဟုတ် ထို့ထက်ပိုသော အမျိုးအစားများ ရှိပါသည်။
• အမျိုးအစားတစ်ခုစီတွင် ကျပန်းကိန်းရှင်တန်ဖိုးတစ်ခုယူသည့်ဖြစ်နိုင်ခြေသည် 0 နှင့် 1 ကြား ဖြစ်ရပါမည်။
• အမျိုးအစားအားလုံးအတွက် ဖြစ်နိုင်ခြေပေါင်းလဒ်သည် 1 အထိ ပေါင်းရပါမည်။

အမျိုးအစားခွဲဝေမှု၏ အထင်ရှားဆုံး ဥပမာမှာ သေတ္တာကို လှိမ့်ခြင်းနှင့် ဆက်စပ်သော ရလဒ်များ ဖြန့်ဖြူးခြင်း ဖြစ်သည်။ K = ဖြစ်နိုင်ချေ 6 ခု ရှိပြီး ရလဒ်တစ်ခုစီ၏ ဖြစ်နိုင်ခြေမှာ 1/6 ဖြစ်သည် ။

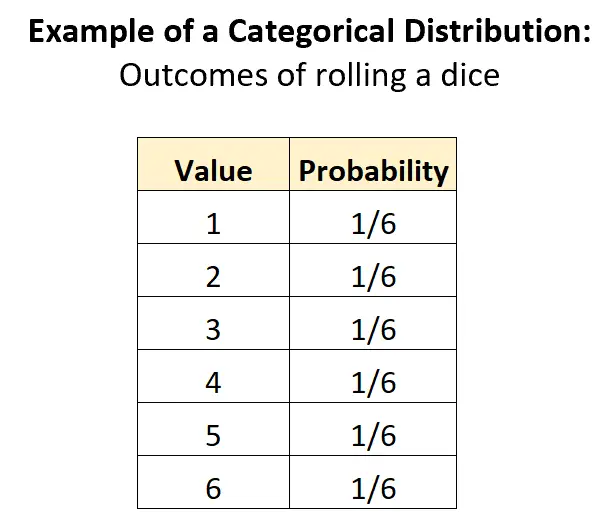
ဤဖြန့်ဖြူးမှုသည် အမျိုးအစားခွဲဝေမှုအဖြစ် ခွဲခြားသတ်မှတ်ရန် စံသတ်မှတ်ချက်များနှင့် ကိုက်ညီသည်-

• အမျိုးအစားများသည် သီးခြားဖြစ်သည် (ဥပမာ ကျပန်းကိန်းရှင်သည် သီးခြားတန်ဖိုးများ – 1၊ 2၊ 3၊ 4၊ 5၊ 6 ကိုသာ ယူနိုင်သည်)
• ဖြစ်နိုင်ချေ အမျိုးအစား နှစ်ခု သို့မဟုတ် ထို့ထက်ပိုသော အမျိုးအစားများ ရှိပါသည်။
• အမျိုးအစားတစ်ခုစီ၏ ဖြစ်နိုင်ခြေသည် 0 နှင့် 1 ကြားဖြစ်သည်။
• ဖြစ်နိုင်ခြေများ၏ ပေါင်းလဒ်သည် 1: 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1 ဖြစ်သည်။

အထွေထွေစည်းမျဉ်း-

ရလဒ်အရေအတွက်ကို ရေတွက် နိုင်လျှင်၊ သင်သည် သီးခြားကျပန်းပြောင်းလဲမှုတစ်ခုဖြင့် လုပ်ဆောင်နေပါသည် – ဥပမာ၊ အကြွေစေ့ခေါင်းပေါ်တက်လာသည့်အကြိမ်အရေအတွက်ကို ရေတွက်ခြင်း။

ဒါပေမယ့် ရလဒ်ကို တိုင်းတာ နိုင်ရင်၊ ဥပမာ- အရပ်၊ အလေးချိန်၊ အချိန် စတာတွေကို တိုင်းတာတဲ့ စဉ်ဆက်မပြတ် ကျပန်းပြောင်းလဲမှုတစ်ခုနဲ့ လုပ်ဆောင်နေပါတယ်။

အမျိုးအစားခွဲဝေမှုဆိုင်ရာ အခြားဥပမာများ

လက်တွေ့ကမ္ဘာတွင် အမျိုးအစားခွဲဝေမှုများစွာ ရှိသည်၊၊

ဥပမာ 1- အကြွေစေ့ကိုလှန်ပါ။

ကျွန်ုပ်တို့သည် အကြွေစေ့ကိုလှန်သောအခါတွင် ဖြစ်နိုင်ချေရှိသော သီးခြားရလဒ် 2 ခုရှိသည်၊ တစ်ခုစီ၏ဖြစ်နိုင်ခြေသည် 0 နှင့် 1 အကြားဖြစ်ပြီး ဖြစ်နိုင်ခြေ၏ပေါင်းလဒ်သည် 1 နှင့် ညီမျှသည်-

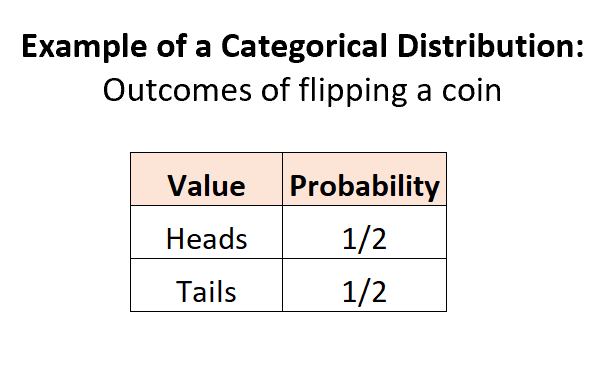
ဥပမာ 2- အိုးထဲတွင် စကျင်ကျောက်များ ရွေးချယ်ခြင်း။

အိုးတစ်လုံးတွင် အနီရောင် စကျင်ကျောက် ၅ လုံး၊ အစိမ်းရောင် စကျင်ကျောက် ၃ လုံးနှင့် ခရမ်းရောင် စကျင်ကျောက် ၂ လုံးပါရှိသည်ဆိုပါစို့။ အကယ်၍ ကျွန်ုပ်တို့သည် အူတွင်းမှဘောလုံးကို ကျပန်းရွေးချယ်ပါက၊ ဖြစ်နိုင်ချေရှိသော သီးခြားရလဒ် 3 ခုရှိသည်၊ တစ်ခုစီ၏ဖြစ်နိုင်ခြေသည် 0 နှင့် 1 ကြားဖြစ်ပြီး ဖြစ်နိုင်ခြေ၏ပေါင်းလဒ်သည် 1 နှင့် ညီမျှသည်-

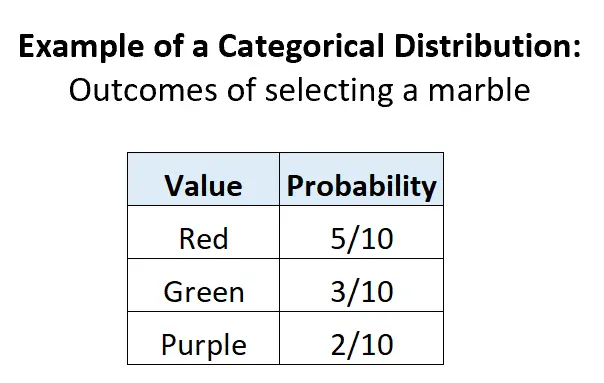
ဥပမာ 3- ကုန်းပတ်တစ်ခုမှ ကတ်တစ်ခုကို ရွေးချယ်ခြင်း။

အကယ်၍ ကျွန်ုပ်တို့သည် စံကတ် 52 ကတ်ထဲမှ ကတ်တစ်ခုကို ကျပန်းရွေးချယ်ပါက၊ ဖြစ်နိုင်ချေ 13 ခု ကွဲပြားသော ရလဒ်များ ရှိသည်၊ ရလဒ်တစ်ခုစီ၏ ဖြစ်နိုင်ခြေသည် 0 နှင့် 1 ကြားဖြစ်ပြီး ဖြစ်နိုင်ခြေများ၏ ပေါင်းလဒ်သည် 1 နှင့် ညီမျှသည်-

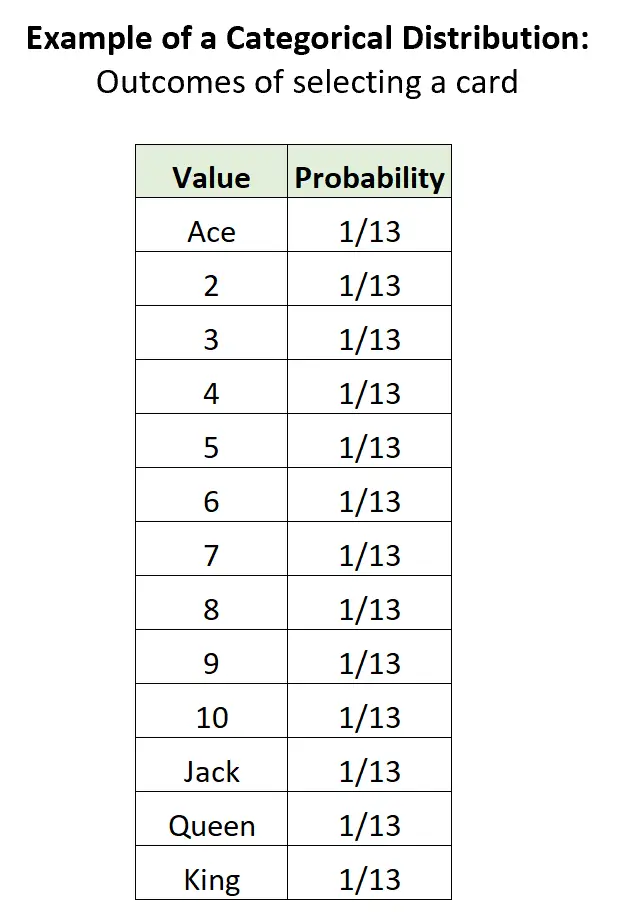
အခြားဖြန့်ဝေမှုများနှင့် ဆက်စပ်မှု

ဖြန့်ဖြူးမှုတစ်ခုကို အမျိုးအစားခွဲဝေမှု အဖြစ် ခွဲခြားသတ်မှတ်ရန်အတွက်၊ ၎င်းတွင် K ≥ 2 ဖြစ်နိုင်ချေရှိသော ရလဒ်များနှင့် n = 1 စမ်းသပ်မှု ရှိရပါမည်။

ဤဝေါဟာရကို အသုံးပြု၍ အမျိုးအစားခွဲဝေမှုတစ်ခုသည် အောက်ပါဖြန့်ဝေမှုများနှင့် ဆင်တူသည်-

Bernoulli ဖြန့်ဖြူးမှု- K = 2 ရလဒ်၊ n = 1 စမ်းသပ်မှု

Binomial ဖြန့်ဖြူးမှု- K = 2 အဆုံးမှတ်များ၊ n ≥ 1 အစမ်း

Multinomial ဖြန့်ဖြူးမှု- K ≥ 2 ရလဒ်များ၊ n ≥ အစမ်း

ထပ်လောင်းအရင်းအမြစ်များ

Random variable တွေက ဘာတွေလဲ။
binomial ဖြန့်ဖြူးခြင်းအကြောင်း နိဒါန်း
Multinomial Distribution နိဒါန်း