Excel တွင် အလယ်အလတ်တန်းစား တွက်ချက်နည်း

ဒေတာအတွဲတစ်ခု၏ အလယ်အလတ်အပိုင်း ကို အောက်ပါအတိုင်း တွက်ချက်သည်။

အလယ်အလတ်တန်းစား = (အကြီးဆုံးတန်ဖိုး + အသေးဆုံးတန်ဖိုး) / ၂

ဤတန်ဖိုးသည် ဒေတာအတွဲအတွင်း အကြီးဆုံးနှင့် အသေးငယ်ဆုံးတန်ဖိုးများ၏ ပျမ်းမျှဖြစ်ပြီး ၎င်းသည် ကျွန်ုပ်တို့အား ဒေတာအတွဲတစ်ခု၏ အလယ်ဗဟိုဖြစ်သည်ကို စိတ်ကူးတစ်ခုပေးသည်။

ဤသင်ခန်းစာသည် Excel ရှိ ဒေတာအစုတစ်ခု၏ အလယ်အလတ်တန်းကို တွက်ချက်နည်းကို ရှင်းပြထားသည်။

ဥပမာ- Excel တွင် အလယ်အလတ်တန်းစား တွက်ချက်ခြင်း။

Excel တွင်အောက်ပါဒေတာအစုံရှိသည်ဆိုပါစို့။

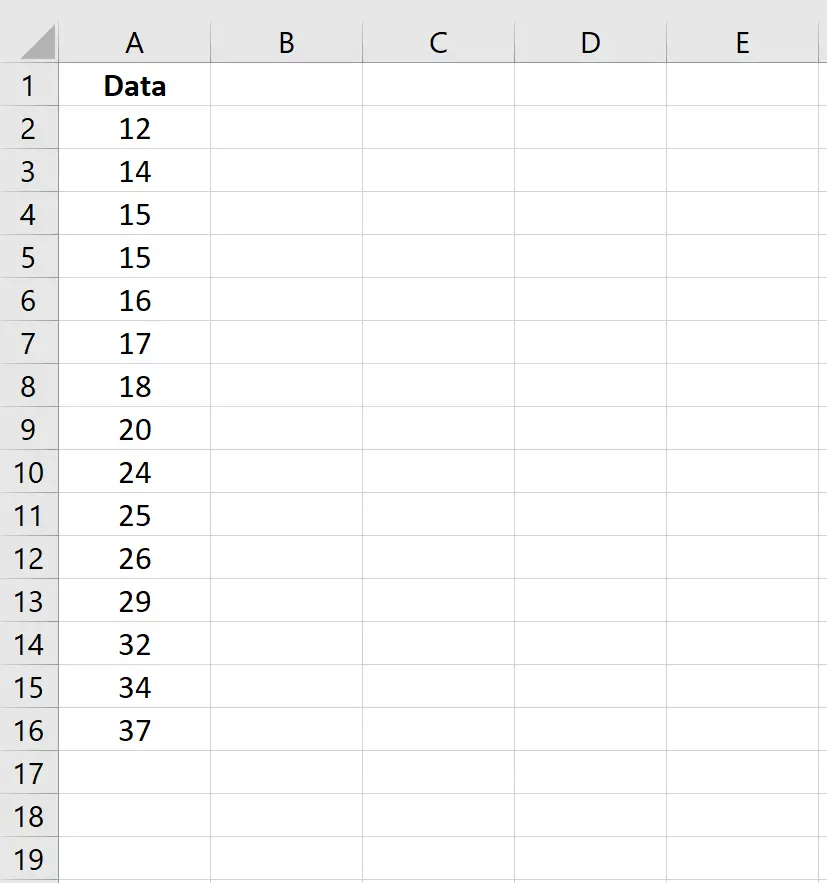
ကြားခံကို တွက်ချက်ရန်၊ ကျွန်ုပ်တို့သည် ရိုးရှင်းသော ဖော်မြူလာကို အသုံးပြုနိုင်သည်။

=(MAX(တန်ဖိုးအပိုင်းအခြား) + MIN(တန်ဖိုးအပိုင်းအခြား)) / 2

ကော်လံ D သည် ကျွန်ုပ်တို့၏ဒေတာအတွဲ၏ အလယ်အလတ်အကွာအဝေးကိုပြသပြီး ကော်လံ E သည် ၎င်းကိုတွက်ချက်ရန်အသုံးပြုသည့်ဖော်မြူလာကိုပြသသည်-

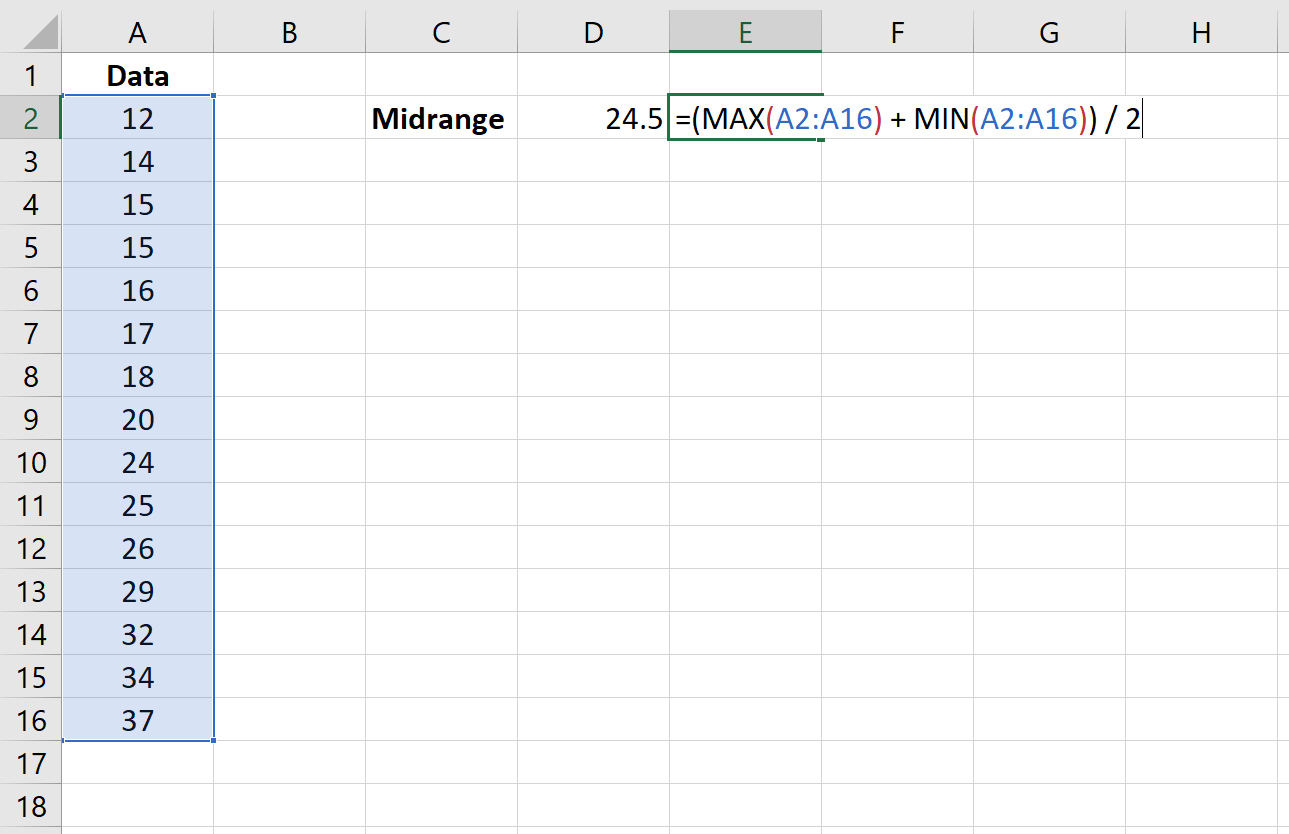
ဤဒေတာအတွဲအတွက် အလယ်အလတ်တန်းစားသည် 24.5 ဖြစ်သည်။

အလယ်အလတ်တန်းစား သုံးခြင်း၏ အားနည်းချက်

ကြားခံများအသုံးပြုခြင်း၏ အားနည်းချက်မှာ ၎င်းတို့ကို outliers များက အလွယ်တကူ လွှမ်းမိုးနိုင်သည်ဟူသော အချက်ဖြစ်သည်။ ဒေတာအတွဲတစ်ခု၏ အနည်းဆုံးတန်ဖိုးသည် ပုံမှန်ထက်သေးငယ်နေပါက သို့မဟုတ် အမြင့်ဆုံးတန်ဖိုးသည် ပုံမှန်မဟုတ်ဘဲ ကြီးမားပါက၊ ၎င်းသည် အလယ်အလတ်တန်းစားတွက်ချက်မှုအပေါ် ကြီးမားသောအကျိုးသက်ရောက်မှုရှိနိုင်သည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့၏ဒေတာအတွဲတွင် အများဆုံးတန်ဖိုးသည် 120 ဖြစ်မဖြစ်ကို သုံးသပ်ပါ။ အလယ်အလတ်တန်းစားသည် 66 ဖြစ်လိမ့်မည်-

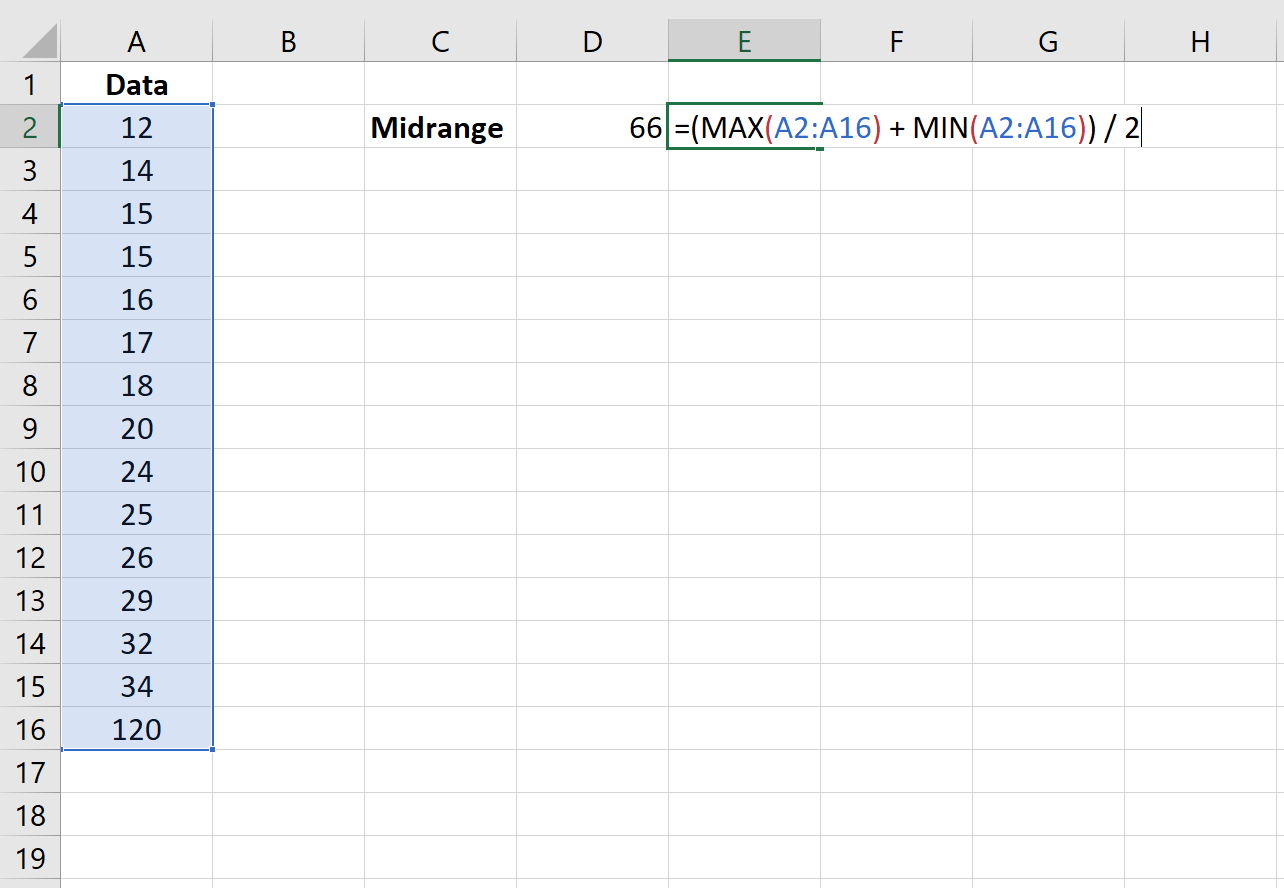
အလယ်အလတ်တန်းစားသည် ဒေတာအစုတစ်ခု၏ အလယ်ဗဟိုသည် အဘယ်မှာရှိသည်ကို ကျွန်ုပ်တို့အား အကြံဉာဏ်ပေးသင့်သည်ဟု မှတ်သားပါ။ သို့သော် ဤအခြေအနေတွင်၊ အမြင့်ဆုံးတန်ဖိုးသည် သာလွန်သောကြောင့်၊ အလယ်အလတ်တန်းစားသည် 66 ဖြစ်ပြီး ကျွန်ုပ်တို့၏ဒေတာအတွဲ၏ဗဟိုနှင့် လုံးဝနီးကပ်မှုမရှိပါ။

Mid-Range Alternatives

လက်တွေ့တွင်၊ အလယ်အလတ်တန်းစားကို ဒေတာအစုတစ်ခု၏ အလယ်ဗဟိုကို တွက်ချက်ရန် နည်းလမ်းတစ်ခုအနေဖြင့် သာလွန်ကောင်းမွန်သော တိုင်းတာမှုများရရှိနိုင်ပြီး အကွာအဝေးများထက် ပိုမိုအားကောင်းသောကြောင့်သာ အသုံးပြုခဲပါသည်။ အထူးသဖြင့်၊ အောက်ဖော်ပြပါ တိုင်းတာမှုနှစ်ခုသည် ပိုမိုတိကျသော ဗဟိုတိုင်းတာမှု ဖြစ်တတ်သည်။

ပျမ်းမျှ- ဒေတာအတွဲတစ်ခုတွင် ပျမ်းမျှတန်ဖိုး။

Median- ဒေတာအတွဲတစ်ခုရှိ ပျမ်းမျှတန်ဖိုး။

အောက်ပါပုံသည် ဒေတာအတွဲ၏ ပျမ်းမျှနှင့် အလယ်အလတ်နှစ်ခုလုံးကို တွက်ချက်ရန် ကျွန်ုပ်တို့အသုံးပြုနိုင်သည့် ဖော်မြူလာများကို ပြသသည်-

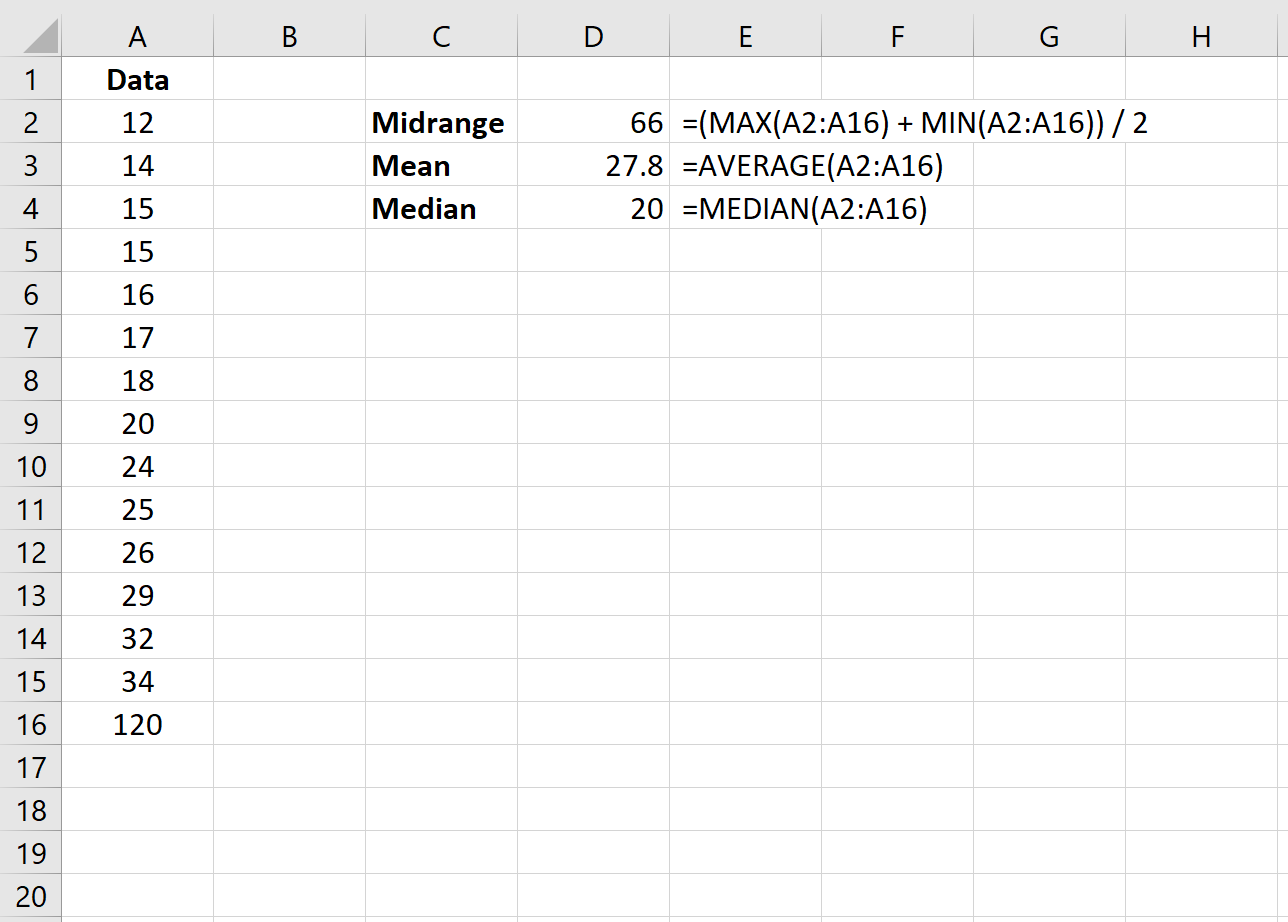
ပျမ်းမျှအား လုံး၀ မထိခိုက်သော်လည်း ပျမ်းမျှအား အနည်းငယ်မျှသာ ထိခိုက်သည်ကို သတိပြုပါ။