အတွဲများပေါ်တွင် လုပ်ဆောင်မှုများ- ပြည်ထောင်စု၊ လမ်းဆုံ၊ ဖြည့်စွက် နှင့် ကွာခြားချက်

အစုံ သည် ဒြပ်စင်များ အစုအဝေးတစ်ခုဖြစ်သည်။

ကျွန်ုပ်တို့သည် စာလုံးကြီးဖြင့် အတွဲတစ်ခုကို သတ်မှတ်ပြီး curly braces များကို အသုံးပြု၍ set ၏ element များကို သတ်မှတ်ပါသည်။ ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့တွင် 1၊ 2၊ 3 ပါရှိသော “ A” ဟုခေါ်သော set တစ်ခုရှိသည်ဆိုပါစို့။ ၎င်းကို အောက်ပါအတိုင်း ရေးပါမည်။

A = {1၊ 2၊ 3}

ဤသင်ခန်းစာတွင် ဖြစ်နိုင်ခြေနှင့် စာရင်းဇယားများတွင် အသုံးအများဆုံး set operations များကို ရှင်းပြထားသည်။

ပြည်ထောင်စု

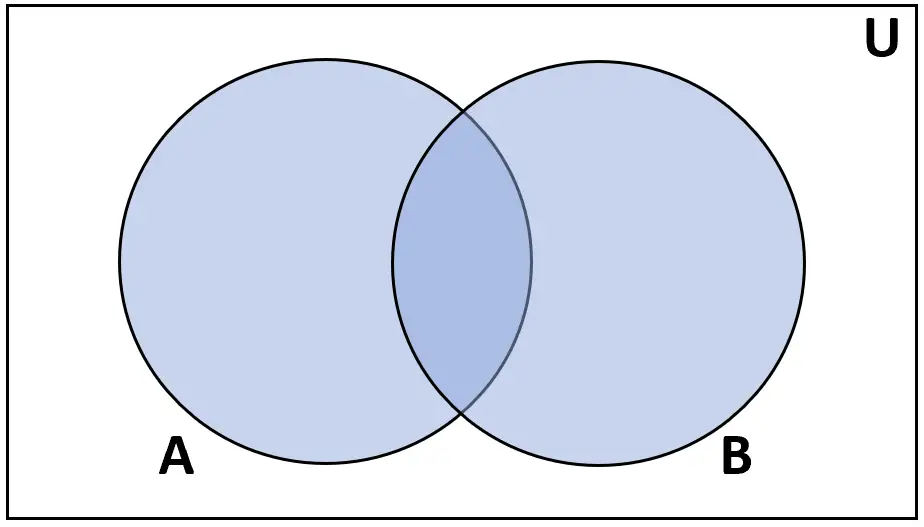
အဓိပ္ပာယ်ဖွင့်ဆိုချက်- A နှင့် B ၏ ပေါင်းစည်းမှု သည် A သို့မဟုတ် B တွင် တွေ့ရသည့် ဒြပ်စင်အစုစုဖြစ်သည်။

အဆင့်သတ်မှတ်ချက်- A ∪ B

ဥပမာများ-

• {1၊ 2၊ 3} ∪ {4၊ 5၊ 6} = {1၊ 2၊ 3၊ 4၊ 5၊ 6}
• {1၊ 2} ∪ {1၊ 2} = {1၊ 2}
• {1၊ 2၊ 3} ∪ {3၊ 4} = {1၊ 2၊ 3၊ 4}

လမ်းဆုံ

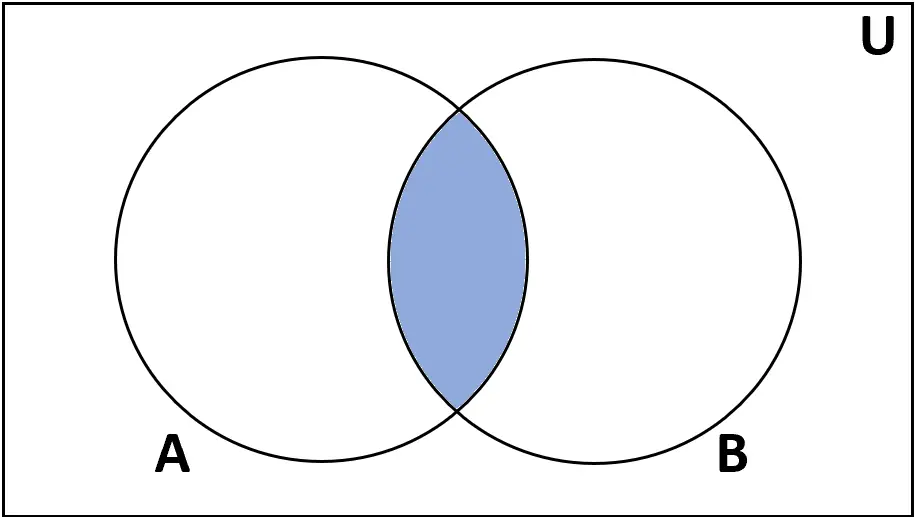
အဓိပ္ပါယ်ဖွင့်ဆိုချက်- အတွဲ A နှင့် B ၏ လမ်းဆုံ သည် A နှင့် B နှစ်ခုလုံးတွင် တွေ့ရသည့် ဒြပ်စင်အစုဖြစ်သည်။

မှတ်ချက်- A ∩ B

ဥပမာများ-

• {1၊ 2၊ 3} ∩ {4၊ 5၊ 6} = {∅}
• {1၊ 2} ∩ {1၊ 2} = {1၊ 2}
• {1၊ 2၊ 3} ∩ {3၊ 4} = {3}

အဖြည့်

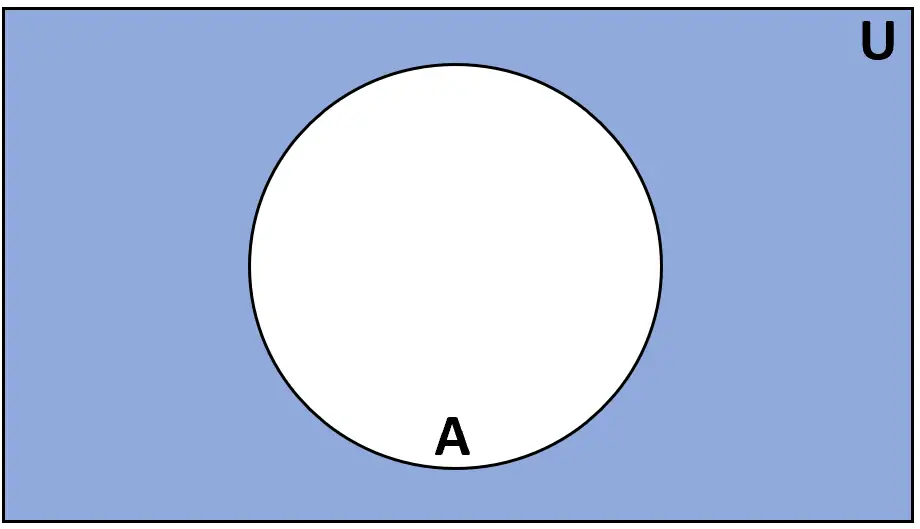
အဓိပ္ပာယ်ဖွင့်ဆိုချက်- set A ၏ ဖြည့်စွက်ချက် သည် universal set U တွင် ပါရှိသော်လည်း A တွင် မပါရှိသော ဒြပ်စင်အစုဖြစ်သည်။

အဆင့်သတ်မှတ်ချက်- A’ သို့မဟုတ် ^Ac

ဥပမာများ-

• U = {1, 2, 3, 4, 5, 6} နှင့် A = {1, 2} ဆိုလျှင် A ^c = {3, 4, 5, 6}၊
• U = {1, 2, 3} နှင့် A = {1, 2} ဆိုလျှင် A ^c = {3}၊

ကွာခြားမှု

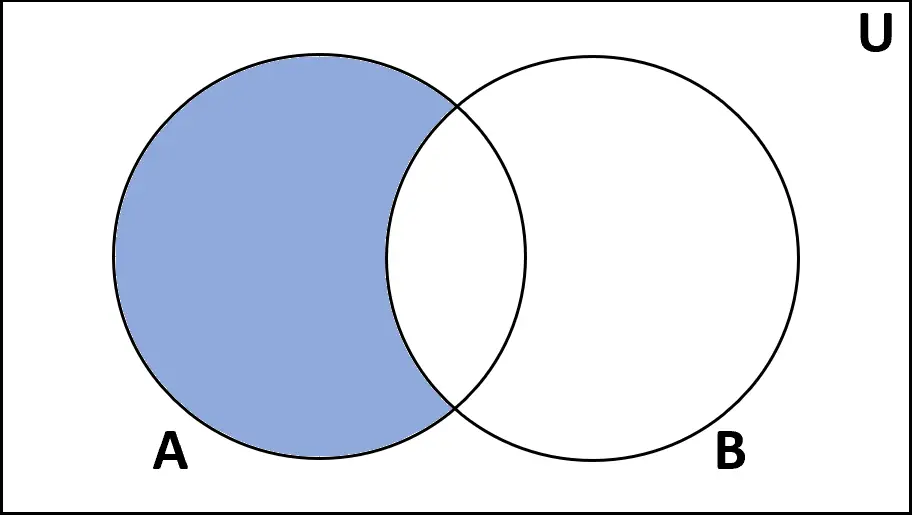
အဓိပ္ပါယ်ဖွင့်ဆိုချက်- A နှင့် B အကြား ကွာခြားချက် မှာ A တွင် တွေ့ရသော်လည်း B တွင် မတွေ့ရသည့် ဒြပ်စင်အစုများဖြစ်သည်။

အဆင့်သတ်မှတ်ချက်များ- A-B

ဥပမာများ-

• {1၊ 2၊ 3} – {2၊ 3၊ 4} = {1}
• {1၊ 2} – {1၊ 2} = {∅}
• {1၊ 2၊ 3} – {4၊ 5} = {1၊ 2၊ 3}

Symmetric ခြားနားချက်

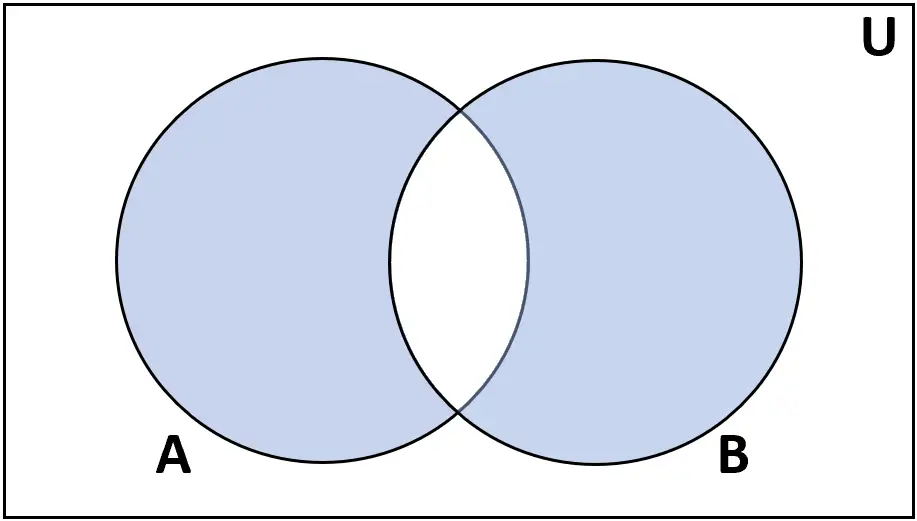
အဓိပ္ပါယ်ဖွင့်ဆိုချက်- အစုံ A နှင့် B ၏ အချိုးညီသော ခြားနားချက် သည် A သို့မဟုတ် B တွင်တွေ့ရသော ဒြပ်စင်အစုများဖြစ်ပြီး နှစ်ခုလုံးမဟုတ်ပေ။

အဆင့်သတ်မှတ်ချက်- AΔB

ဥပမာများ-

• {1, 2, 3} Δ {2, 3, 4} = {1, 4}၊
• {1, 2} Δ {1, 2} = {∅}
• {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}

Cartesian ထုတ်ကုန်

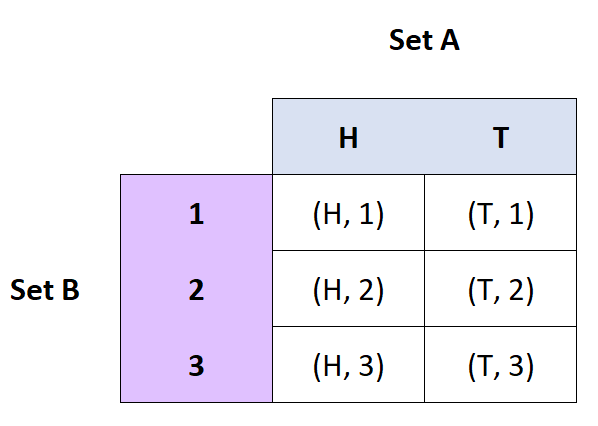
အဓိပ္ပါယ်ဖွင့်ဆိုချက်- A နှင့် B အတွဲများ၏ Cartesian ထုတ်ကုန် သည် A နှင့် B အတွဲများဖြစ်သည်။

အဆင့်သတ်မှတ်ချက်- A x B

ဥပမာများ-

• အကယ်၍ A = {H, T} နှင့် B = {1, 2, 3}, ထို့နောက် A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( T, 2), (T, 3)}၊
• အကယ်၍ A = {T, H} နှင့် B = {1, 2, 3}, ထို့နောက် A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( ဇ၊ ၂) (H၊ ၃)}၊